PageRank算法原理与Python实现
1 PageRank算法简介
PageRank算法,即网页排名算法,由Google创始人Larry Page在斯坦福上学的时候提出来的。该算法用于对网页进行排名,排名高的网页表示该网页被访问的概率高。
该算法的主要思想有两点:
如果多个网页指向某个网页A,则网页A的排名较高。
如果排名高A的网页指向某个网页B,则网页B的排名也较高,即网页B的排名受指向其的网页的排名的影响。
2 PageRank算法原理
2.1 简单的PageRank算法
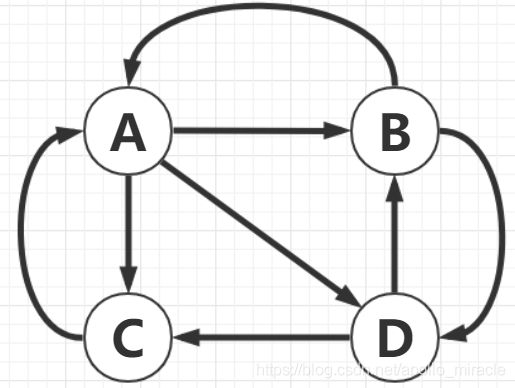
如图是一个4个网页之间的链接情况:
假设网页X的排名用PR(X)表示,则A的排名为PR(A),由图可知,网页B和C指向了网页A,那么网页A的排名可以表示为:
![]()
网页C只指向了A,不指向其他网页,然而网页B不仅指向了A,还指向了D,因此上面的公式更合理地修改为:
![]()
意思是,B的PageRank值被分给了A和D,而C的PageRank值全都给了A。
2.2 考虑没有出边(outlink)的网页
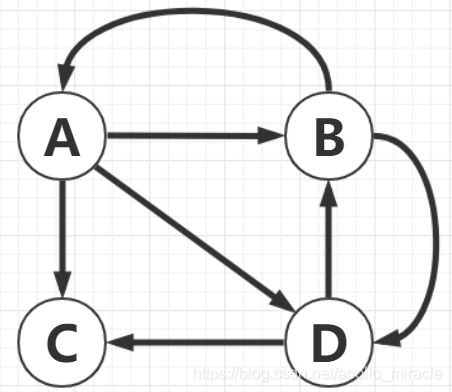
有的网页,没有指向其他网页,如下图中的C网页。
那么,假设网页C的PageRank值被均分为到图中的所有网页(4个网页),那么A网页的PageRank值可以表示为:
![]()
2.3 网页链接中存在环
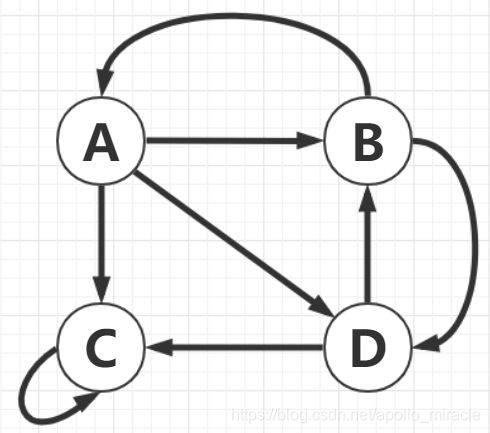
图中网页C指向网页C,不指向其他网页。现实中,网页自己指向自己的情况可能不太常见,但是有可能的情况是:若干个页面形成一个环,那么用户在进入其中某个网页的时候,就陷入这个循环中。
假设当一个用户,遇上这种情况时,以某个概率α随机指向其他任意一个网页,每个网页的概率相等。因此上图中的网页A的PageRank值可以表示为:
![]()
上面这个公式可以解释为:α表示用户从网页B以概率α链接到网页A,后面的(1-α)表示用户从网页C以概率(1-α)链接到网页A。
即:
网页B的PageRank值分配情况为:α*1/2给A,α*1/2给D,(1-α)/4分别给4个网页。
网页C的PageRank值分配情况为:α*1给自己C(1-α)*1/4分别给其他网页。
2.4 更一般的PageRank公式
综合上面的论述,一般的PageRank计算公式为:
![]()
其中S(X)表示,指向网页X的所有网页的集合,n_i表示网页Y_i的出边数量,N表示所有网页总数,α一般取0.85。
3 PageRank值的计算方法
3.1 迭代法
利用前面得到的公式,进行迭代,直到迭代前后两次的差值在允许的阈值范围内,迭代结束。
当然,可以将迭代过程写成矩阵形式。推导过程如下:
针对前面的最后一个网络图,可以分别得到各个网页的PageRank值得计算公式,如下:
![]()
![]()
![]()
![]()
写成矩阵的形式为:
可以将上面的列向量和矩阵分别记为一些符号,上式表示为:
![]()
还有更简洁的记法,记
![]()
A是一个常数矩阵,那么,就有迭代公式:
![]()
也可以根据这个公式,进行迭代。
3.2 代数法
因为,PageRank算法最终收敛(这个结论可以证明,此文不证明),因此,收敛时刻的PageRank 值组成的列向量P应当满足:
![]()
因此有:
![]()
这个方法不用迭代,求出矩阵的逆,就可以求出PageRank值组成的列向量P(然而,计算大规模的矩阵的逆,也是个难题。因此,这个方法代码简单,但效率可能不如迭代方法高)
4 Python实现
下面仅仅实现迭代法,代码如下,需要用到Python的numpy库用于矩阵乘法:
# 输入为一个*.txt文件,例如
# A B
# B C
# B A
# ...表示前者指向后者
import numpy as np
# 读入有向图,存储边
with open('input_1.txt', 'r') as f:
content = f.readlines()
edges = [line.strip('\n').split(' ') for line in content]
print(edges)
# 根据边获取节点的集合
nodes = []
for edge in edges:
if edge[0] not in nodes:
nodes.append(edge[0])
if edge[1] not in nodes:
nodes.append(edge[1])
print(nodes)
N = len(nodes)
# 将节点符号(字母),映射成阿拉伯数字,便于后面生成A矩阵/S矩阵
node_to_num = {}
for i, node in enumerate(nodes):
node_to_num[node] = i
for edge in edges:
edge[0] = node_to_num[edge[0]]
edge[1] = node_to_num[edge[1]]
print(edges)
# 生成初步的S矩阵
S = np.zeros([N, N])
for edge in edges:
S[edge[1], edge[0]] = 1
print(S)
# 计算比例:即一个网页对其他网页的PageRank值的贡献,即进行列的归一化处理
for j in range(N):
sum_of_col = sum(S[:, j])
for i in range(N):
S[i, j] /= sum_of_col
print(S)
# 计算矩阵A
alpha = 0.85
A = alpha * S + (1 - alpha) / N * np.ones([N, N])
print(A)
# 生成初始的PageRank值,记录在P_n中,P_n和P_n1均用于迭代
P_n = np.ones(N) / N
P_n1 = np.zeros(N)
e = 100000 # 误差初始化
k = 0 # 记录迭代次数
print('loop...')
while e > 0.000000001: # 开始迭代
P_n1 = np.dot(A, P_n) # 迭代公式
e = P_n1 - P_n
e = max(map(abs, e)) # 计算误差
P_n = P_n1
k += 1
print('iteration %s:' % str(k), P_n1)
print('final result:', P_n)输入的input_1.txt文本内容为:
A B
A C
A D
B D
C E
D E
B E
E A结果为:
最后的一个数组,分别为A, B, C, D, E的PageRank值,其中E最高, A第二高, B和C相同均最低。
可以看出,有3条边指向E。再看,指向A的这个点是E点,因此A的PageRank值也很高,可以说“A沾了E的光”。
上面的可视化代码如下:
import networkx as nx
import matplotlib.pyplot as plt
# 读入有向图,存储边
f = open('input_1.txt', 'r')
edges = [line.strip('\n').split(' ') for line in f]
G = nx.DiGraph()
for edge in edges:
G.add_edge(edge[0], edge[1])
nx.draw(G, with_labels=True)
plt.show()