算法学习—排序
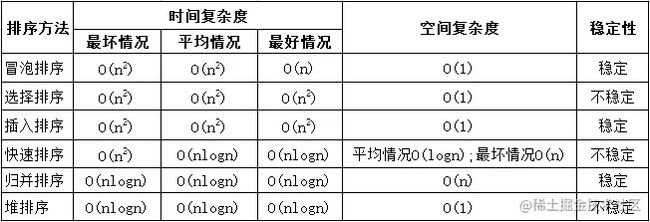
排序算法
一、选择排序
1.算法简介
选择排序是一个简单直观的排序方法,它的工作原理很简单,首先从未排序序列中找到最大的元素,放到已排序序列的末尾,重复上述步骤,直到所有元素排序完毕。
2.算法描述
1)假设未排序序列的第一个是最大值,记下该元素的位置,从前往后比较
2)若某个元素比该元素大,覆盖之前的位置
3)重复第二个步骤,直到找到未排序的末尾
4)将未排序元素的第一个元素和最大元素交换位置
5)重复前面几个步骤,直到所有元素都已经排序。
3.算法分析
选择排序的交换操作次数最好情况已经有序为0次,最坏情况逆序n-1次,因此交换操作次数位于0(n-1)次之间;比较操作次数(n-1+…+2+1+0)为n(n-1)/2次;交换元素赋值操作为3次,逆序需要n-1趟交换,因此,赋值操作位于03(n-1)次之间。由于需要交换位置,所以肯定是不稳定的。
时间复杂度均为o(n^2) 空间复杂度为o(1) 不稳定
4.代码实现
//选择排序
function selsetSort(arr){
var len = arr.length;
for(var i=0;i<len-1;i++){
for(var j=i+1;j<len;j++){
if(arr[i] > arr[j]){//寻找最小值
var temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
}
return arr;
}
二、冒泡排序
1.算法简介
列表每两个相邻的数进行比较,如果前面的数比后面的数大,则交换这两个数,一轮排序完成后,则无序区减少一个数,有序区增加一个数。
2.算法描述
1)快速排序的特点就是随机设置一个基准点,比如是数组的第一个元素,然后数组的其他元素就跟这个基准线进行对比,比基准线大的放在左边,比基准线小的放在右边
2)再设置一个基准线,再这样小的放左边,大的放右边,递归。
3.算法分析
平均时间复杂度O(nn) 、最好情况O(n)、最差情况O(nn)
空间复杂度O(1) 稳定
4.代码实现
function sort(arr){
let len = arr.length;
for (let i = 0; i < len - 1 ; i++) {
// 用来标记在一轮冒泡过程中有无交换过
let flag = false;
for (let j = 0; j < len - i; j++) {
if(arr[j] > arr[j+1]){
// 交换两个数
let temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
flag = true;
}
}
// 如果在一轮冒泡过程中没有交换过,说明此时的列表已经是排序好的了,直接结束循环
if(!flag){
return;
}
}
}
let arr = [2,3,1,4,8,7,9,6];
this.sort(arr;
console.log(arr);
三、插入排序
1.算法简介
所谓插入排序,就是把最小的(或者最大的),一次次插入到最前面,从而达到排序的效果
2.算法描述
刚开始将整个数组看作一个无序区,每一轮拿无序区的第一数与有序区的数从后往前依次进行比较,遇到更大的数则交换,每一轮排序完成后,有序区增加一个数,无序区减少一个数。
3.算法分析
时间复杂度是O(n*n) 空间复杂度为o(1) 稳定
4.代码实现
function sort(arr){
let len = arr.length;
for (let i = 1; i < len; i++) {
for (let j = i - 1; j >= 0 ; j--) {
if(arr[j] > arr[j+1]){
let temp = arr[j+1]
arr[j+1] = arr[j]
arr[j] = temp
}
}
}
},
四、快速排序
1.算法简介
采用“分治”的思想,对于一组数据,选择一个基准元素(base),通常选择第一个或最后一个元素,通过第一轮扫描,比base小的元素都在base左边,比base大的元素都在base右边,再有同样的方法递归排序这两部分,直到序列中所有数据均有序为止。快速排序算法的性能比冒泡、选择排序都要好,和归并排序一样,是一个可以用于实战的算法。
2.算法描述
1)快速排序的特点就是随机设置一个基准点,比如是数组的第一个元素,然后数组的其他元素就跟这个基准线进行对比,比基准线大的放在左边,比基准线小的放在右边
2)再设置一个基准线,再这样小的放左边,大的放右边,递归。
3.算法分析
时间复杂度是O(nlogn) 空间复杂度为o(logn) 不稳定
4.代码实现
function sort(arr,l,r){
if(l < r){
let i = l;
let j = r;
let mid = arr[l];
while(i < j){
while(arr[j] > mid && i < j){
j--;
}
arr[i] = arr[j];
while(arr[i] < mid && i < j){
i++;
}
arr[j] = arr[i];
}
arr[i] = mid
this.test(arr,l,i-1)
this.test(arr,i+1,j)
return arr
}else{
return
}
},
// 测试数据
let arr = [2,3,1,4,8,7,9,6];
let res = this.sort(arr,0,7);
console.log(res);
五、归并排序
1.算法简介
使用分而治之的概念对给定的元素列表进行排序。它将问题分解为较小的子问题,直到它们变得足够简单以至可以直接解决为止。
2.算法描述
1)将给定的列表分为两半(如果列表中的元素数为奇数,则使其大致相等)。
2)以相同的方式继续划分子数组,直到只剩下单个元素数组。
3)从单个元素数组开始,合并子数组,以便对每个合并的子数组进行排序。
4)重复第 3 步单元,直到最后得到一个排好序的数组。
3.算法分析
时间复杂度是O(nlogn) 空间复杂度为O(n) 稳定
4.代码实现
function sort(arr){
if(arr && arr.length > 1){
const mid = Math.floor(arr.length/2)
const left = arr.slice(0,mid)
const right = arr.slice(mid);
return this.merge(this.sort(left), this.sort(right))
}
return arr
},
function merge(leftList, rightList){
const newList = [];
const leftLength = leftList && leftList.length;
const rightLength = rightList && rightList.length;
let i = 0;
let j = 0;
while (i < leftLength && j < rightLength) {
if (leftList[i] < rightList[j]) {
newList.push(leftList[i++]);
} else {
newList.push(rightList[j++]);
}
}
while (i < leftLength) {
newList.push(leftList[i++]);
}
while (j < rightLength) {
newList.push(rightList[j++]);
}
return newList;
},
六、堆排序
1.算法简介
堆是一种特殊的完全二叉树,堆分为大根堆和小根堆,满足任一节点都比其孩子节点大的一个完全二叉树就是大根堆,满足任一节点都比其孩子节点小的一个完全二叉树就是小根堆。
2.算法描述
首先构造一个大根堆(此时整个堆是无序区),然后将堆顶的元素取出放到有序区(也就是数组的最后),然后将堆的最后一个元素(也就是无序区的最后一个元素)放到堆顶,堆就少了一个元素,此时通过一次向下调整重新使堆有序,调整后的堆顶就是整个数组的第二大元素,然后重复之前的操作依次将元素放到有序区,直到堆变空,便可得到排序好的数组。
3.算法分析
时间复杂度是O(nlogn) 空间复杂度为O(1) 不稳定
4.代码实现
function sort(list) {
if (list && list.length > 1) {
const len = list.length;
// 首先构造大根堆,从最后一个不是叶子节点的节点开始遍历,从后往前依次进行向下调整
for (let i = Math.floor((len-2)/2); i>=0; i--) {
sift(list, i, len-1);
}
// 然后将堆的第一元素与有序区的第一个元素进行交换,此时有序区增加一个,无序区减少一个,再进行一次堆的向下调整,然后重复上述操作,最终使整个数组有序
for(let i = len-1; i>=0; i--){
const m = list[0];
list[0] = list[i];
list[i] = m;
sift(list, 0, i-1);
}
}
}
/**
* 堆的向下调整
* 先从根节点开始,如果孩子节点比父节点大,则将该孩子节点赋值给父节点
* 然后指针指向下一层,重复上面的操作,直到找到孩子节点没有比父节点大的节点,终止循环
* 最后将原始的根节点赋值给当前父节点
*/
function sift(li, low, high) {
const tmp = li[low]; // 缓存根节点
let i = low; // 当前的父节点,最开始指向根节点
let j = i*2+1; // 当前的孩子节点,最开始指向根节点的左孩子节点
while (j <= high) {
// 如果有右孩子节点且比左孩子节点大,则j指向右孩子节点
if (j+1 <= high && li[j+1] > li[j]) {
j++;
}
if (li[j] > tmp) {
li[i] = li[j]; // 将较大的孩子节点赋值给父节点
i = j; // i指向下一层
j = i*2 +1;
} else {
break; // 如果当前子节点没有比原始根节点大,结束循环
}
}
li[i] = tmp; // 最后将原始的根节点赋值给当前父节点
}