❤️详解「 A*」算法原理及其算法实现(C/C++描述)

目录

定义和概念

原理步骤

算法推演

算法源码

---

定义和概念

A*算法，A*（A-Star)算法是一种静态路网中求解最短路径最有效的直接搜索方法，也是解决许多搜索问题的有效算法。算法中的距离估算值与实际值越接近，最终搜索速度越快（百度百科）

百科百科将A*算法定义为求解最短路径，我认为不够严谨。

A*算法较之传统的路径规划算法,实时性更高、灵活性更强,寻路结果更加接近人工选择的路径结果. A*寻路算法 并不是找到最优路径，只是找到 相对近的路径，因为找最优要把所有可行路径都找出来进行对比，消耗性能太大， 寻路效果只要相对近路径就行了。

也因此在静态路网的寻路问题中A*算法被大量运用。

A*算法重要的三个指标 G、H、 F

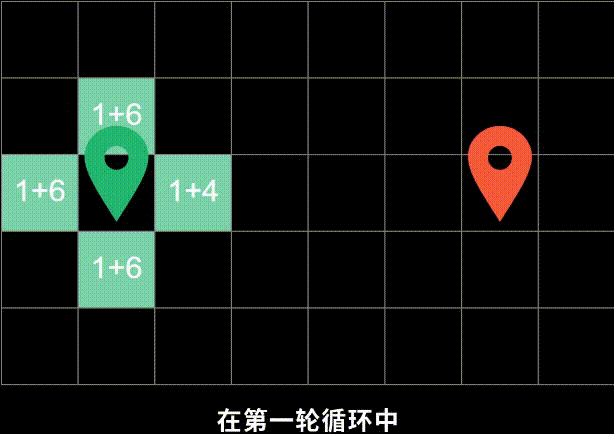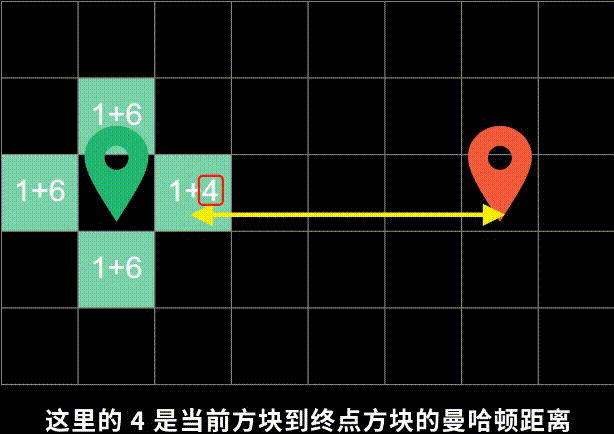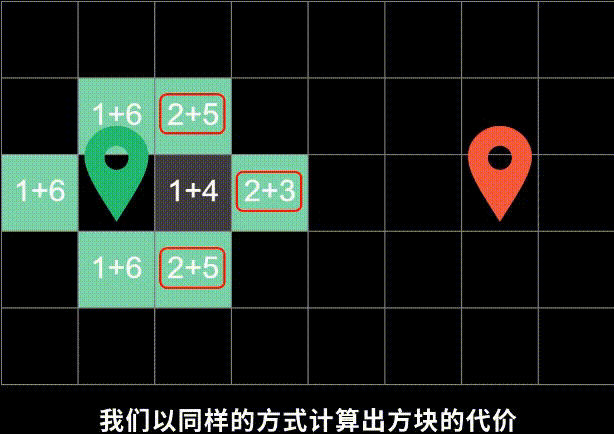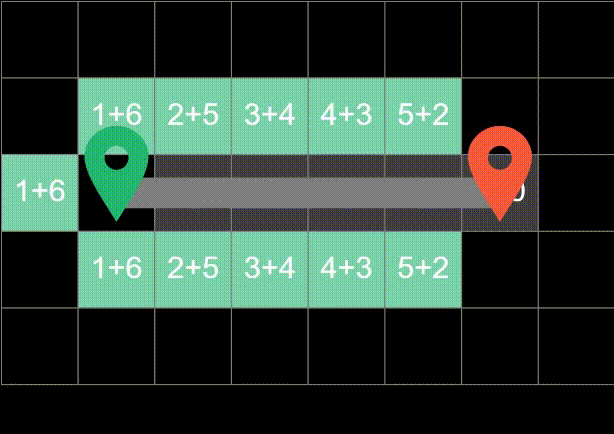
G 表示从起点移动到终点的移动距离

H 表示从指定的地点移动到终点的预计移动距离

F = G + H ，F 即表示从起点经过此点预计到终点的总移动距离

距离有两个指标：

曼哈顿距离：两个点在标准坐标系上的绝对轴距总和。计算公式：|x1-x2|+|y1-y2|

欧式距离：两个点的直线距离 。计算公式： 

原理步骤

A*算法首先定义两个重要的链表：openList、closeList

通过循环将可能到达的结点加入openList，已经走过的结点加入closeList

1）动态展示

2）静态展示

1. 从起点开始, 把它作为待处理的方格存入一个预测可达的节点列表，简称 openList, 即把起点放入“预测可达节点列表”， 可达节点列表 openList 就是一个等待检查方格的列表。

2. 寻找 openList 中 F 值最小的点 min（一开始只有起点）周围可以到达的方格（可到达的意思是其不是障碍物，也不存 在关闭列表中的方格,即不是已走过的方格）。计算 min 周围可到达的方格的 F 值。将还没在 openList 中点放入其中, 并 设置它们的"父方格"为点 min,表示他们的上一步是经过 min 到达的。如果 min 下一步某个可到达的方格已经在 openList 列表那么并且经 min 点它的 F 值更优,则修改 F 值并把其"父方格"设为点 min。

3. 把 2 中的点 min 从"开启列表"中删除并存入"关闭列表"closeList 中, closeList 中存放的都是不需要再次检查的方格。如 果 2 中点 min 不是终点并且开启列表的数量大于零，那么继续从第 2 步开始。如果是终点执行第 4 步，如果openList 列表数量为零，那么就是找不到有效路径。

4.如果第 3 步中 min 是终点，则结束查找，直接追溯父节点到起点的路径即为所选路径。

算法推演

1）二维图中结点数据结构可定义为：

typedef struct _Point
{
	int x, y;
	int F, G, H;//F=G+H
	struct _Point *parent;
}Point;

2）找出目标结点

static Point *FindPath(Point *startPoint, Point *endPoint)
{
	openList.push_back(AllocPoint(startPoint->x,startPoint->y));

	while (!openList.empty())
	{
		//1.第一步 取openlist中的F最小值
		Point *curPoint = GetLeastPoint();

		//2.将当前结点加入到closelist中
		openList.remove(curPoint);
		closeList.push_back(curPoint);

		//3.找到当前结点周围可达的节点 并计算F值
		vectorsurroundPoints = GetSurroundPoints(curPoint);
		for (vector::const_iterator it= surroundPoints.begin();it!= surroundPoints.end();it++)
		{
			Point *target = *it;
			Point *exsit = isInList(openList, target);
			if (!exsit)//如果可达结点不在openList中，则直接加入openList链表
			{
				target->parent = curPoint;
				target->G = calcDistance(curPoint, target);
				target->H = calcDistance(target, endPoint);
				target->F = target->G + target->H;
				openList.push_back(target);
			}
			else
//如果可达结点已经在openList中，则重新计算F值，如果小于原F值，则改变其父节点为当前结点，G、F
//值随之改变
			{
				int tmpG = calcDistance(curPoint, target);
				if (tmpGG)
				{
					exsit->parent = curPoint;
					exsit->G = tmpG;
					exsit->F = tmpG + exsit->H;
				}
				
				delete target;
			}
		}
		surroundPoints.clear();
		Point *resPoint = isInList(openList, endPoint);
		if (resPoint)
			return resPoint;
	}

}

3）通过目标结点的父节遍历链表找到开始结点，以获得正确路径

/*返回正确路径*/
list GetPath(Point *startPoint, Point *endPoint)
{
	Point *result = FindPath(startPoint, endPoint);

	list path;

	//返回路径，如果没有找到路径则返回空链表
	while (result)
	{
		path.push_front(result);
		result = result->parent;
	}
	return path;
}

 算法源码

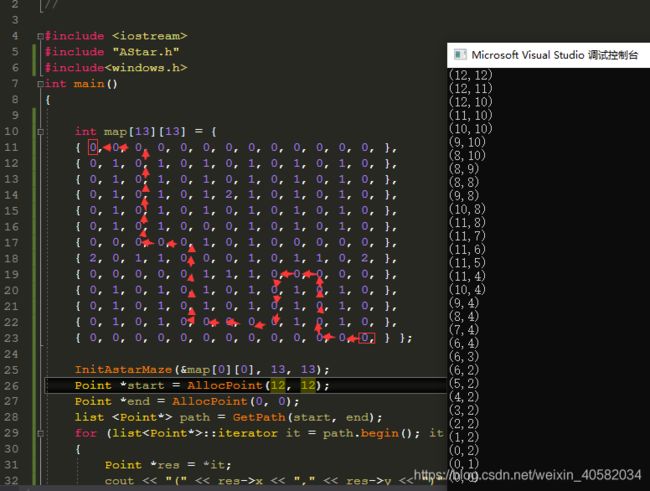
 运行截图：

由此也可知，A*算法所得结果并非最短路径

AStar.h

#pragma once
#include
#include

using namespace std;

const int kCost1 = 10;//直移一格消耗
const int kCost2 = 14;//斜移一格消耗

typedef struct _Point
{
	int x, y;
	int F, G, H;//F=G+H
	struct _Point *parent;
}Point;

/*分配一个格子*/
Point *AllocPoint(int x, int y);
/*初始化地图*/
void InitAstarMaze(int *Maze, int lines, int colums);
/*A*算法寻找路径*/
list GetPath(Point *startPoint, Point *endPoint);
/*清理资源*/
void ClearAstarMaze();

AStar.cpp

#include
#include"AStar.h"
#include 
#include 

static int *maze;//地图
static int cols;//列数
static int lines;//行数

static listopenList;
static listcloseList;

/*A*算法寻找路径*/
Point * isInList(const list point, const Point *target);
static Point *GetLeastPoint();//找出openlist中F值最小的节点
static vector GetSurroundPoints(const Point *point);//找到当前结点周围可达的节点
bool isCanreach(const Point *point, const Point *target);//判断这两点是否可达
int calcDistance(Point *target, Point *endPoint);
static Point *FindPath(Point *startPoint, Point *endPoint)
{
	openList.push_back(AllocPoint(startPoint->x,startPoint->y));

	while (!openList.empty())
	{
		//1.第一步 取openlist中的F最小值
		Point *curPoint = GetLeastPoint();

		//2.将当前结点加入到closelist中
		openList.remove(curPoint);
		closeList.push_back(curPoint);

		//3.找到当前结点周围可达的节点 并计算F值
		vectorsurroundPoints = GetSurroundPoints(curPoint);
		for (vector::const_iterator it= surroundPoints.begin();it!= surroundPoints.end();it++)
		{
			Point *target = *it;
			Point *exsit = isInList(openList, target);
			if (!exsit)
			{
				target->parent = curPoint;
				target->G = calcDistance(curPoint, target);
				target->H = calcDistance(target, endPoint);
				target->F = target->G + target->H;
				openList.push_back(target);
			}
			else
			{
				int tmpG = calcDistance(curPoint, target);
				if (tmpGG)
				{
					exsit->parent = curPoint;
					exsit->G = tmpG;
					exsit->F = tmpG + exsit->H;
				}
				
				delete target;
			}
		}
		surroundPoints.clear();
		Point *resPoint = isInList(openList, endPoint);
		if (resPoint)
			return resPoint;
	}

}

void InitAstarMaze(int *arr,int _lines, int colums)
{
	maze = arr;
	cols = colums;
	lines = _lines;
}

Point * AllocPoint(int x, int y)
{
	Point * tmp = new Point;
	memset(tmp, 0, sizeof(Point));
	tmp->x = x;
	tmp->y = y;
	return tmp;
}

/*返回正确路径*/
list GetPath(Point *startPoint, Point *endPoint)
{
	Point *result = FindPath(startPoint, endPoint);

	list path;

	//返回路径，如果没有找到路径则返回空链表

	while (result)
	{
		path.push_front(result);
		result = result->parent;
	}

	return path;
}

static Point *GetLeastPoint()
{
	Point *resPoint = openList.front();
	if (!openList.empty())
	{

		for (list::const_iterator it= openList.begin();it!=openList.end();it++)
		
			if ((*it)->F < resPoint->F)
			{
				resPoint = *it;
			}
	}
	
	return resPoint;
}

static vector GetSurroundPoints(const Point *point)
{
	vector surroundPoints;
	
	for (int x= point->x-1;x<= point->x+1;x++)
		for (int y = point->y - 1; y <= point->x+1; y++)
	{
			Point *tmp = AllocPoint(x, y);
			if (isCanreach(point,tmp))
			{
				surroundPoints.push_back(tmp);
			}
			else
			{
				delete tmp;
			}
	}
	return surroundPoints;
}

Point * isInList(const list point,const Point *target)
{
	for (list::const_iterator it = point.begin(); it != point.end(); it++)
	{
		if ((*it)->x==target->x && (*it)->y==target->y)
		{
			return *it;
		}
	}
	return NULL;
}
bool isCanreach(const Point *point, const Point *target)
{
	if (target->x<0|| target->x>(lines-1)
		|| target->y<0|| target->y>(cols-1)
		|| maze[target->x*cols+target->y]==1//1代表无法走的格子
		|| maze[target->x*cols + target->y] == 2//2代表无法走的格子
	    || (target->x==point->x && target->y==point->y)
		|| isInList(closeList,target)!=NULL)
	{
		return false;
	}

	if (abs(point->x - target->x) + abs(point->y - target->y) == 1)
		return true;
	else
		return false;
}


int calcDistance(Point *target, Point *endPoint)
{
	return abs(target->x - endPoint->x) + abs(target->y - endPoint->y);
}

void ClearAstarMaze()
{
	maze = NULL;
	lines = cols = 0;
	for (list::iterator it=openList.begin();it!=openList.end();)
	{
		delete *it;
		it = openList.erase(it);
	}

	for (list::iterator it = closeList.begin(); it != closeList.end();)
	{
		delete *it;
		it = closeList.erase(it);
	}
}

main.cpp

#include 
#include "AStar.h"
#include
int main()
{
	
	int map[13][13] = { 
	{ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, }, 
	{ 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, },
	{ 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, }, 
	{ 0, 1, 0, 1, 0, 1, 2, 1, 0, 1, 0, 1, 0, }, 
	{ 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, }, 
	{ 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, },
	{ 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, }, 
	{ 2, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 2, }, 
	{ 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, }, 
	{ 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, }, 
	{ 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, },
	{ 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, }, 
	{ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, } };
	
	InitAstarMaze(&map[0][0], 13, 13);
	Point *start = AllocPoint(12, 12);
	Point *end = AllocPoint(0, 0);
	list  path = GetPath(start, end);
	for (list::iterator it = path.begin(); it != path.end(); it++)
	{
		Point *res = *it;
		cout << "(" << res->x << "," << res->y << ")" << endl;
		Sleep(800);	
	}
	ClearAstarMaze();
}