智能优化算法-理论
一、常用的无约束优化方法
1. 最速下降法:
负梯度方向使目标函数下降最快
2.牛顿法
二、分类
1. 兔子理论:
为了找出地球上最高的山,一群兔子开始想办法。
(1)局部搜索:
兔子朝着比现在高的地方跳去。他们找到了不远处的最高山峰。但是这座山不一定是珠穆朗玛峰。这就是局部搜索,它不能保证局部最优值就是全局最优值。
(2)模拟退火:
兔子喝醉了。他随机地跳了很长时间。这期间,它可能走向高处,也可能踏入平地。但是,他渐渐清醒了并朝最高方向跳去。这就是模拟退火。
(3) 遗传算法:
兔子们吃了失忆药片,并被发射到太空,然后随机落到了地球上的某些地方。他们不知道自己的使命是什么。但是,如果你过几年就杀死一部分海拔低的兔子,多产的兔子们自己就会找到珠穆朗玛峰。这就是遗传算法。
(4)禁忌搜索:
兔子们知道一个兔的力量是渺小的。他们互相转告着,哪里的山已经找过,并且找过的每一座山他们都留下一只兔子做记号。他们制定了下一步去哪里寻找的策略。这就是禁忌搜索。
2. 群体智能:
粒子群算法、蚁群算法等。
3. 神经网络
三、神经网络
1.BP
BP算法是一种监督式学习算法,属于学习算法的推广。其目的是使网络输出层的误差平方和达到最小,由信息的正向传播与误差的反向传播两部分组成。
采用最速下降法,但收敛速度较慢,易陷入局部极小点
2. 改进的BP
主要有采用启发式信息技术的BP算法,加入数值优化技术的BP算法和基于现代优化理论的BP算法三大类。 如牛顿法、共轭梯度法, 基于现代优化理论的BP算法是将遗传算法(简称GA)、蚁群算法(简称CA)、模拟退火算法(简称SA算法)等与神经网络相结合,改善BP算法的缺陷,提高算法的全局收敛能力。
3. 应用
(1)模式识别
神经网络经过训练可有效地提取信号、语音、图像、雷达、声纳等感知模式的特征,主要用于特征提取、聚类分析、边缘检测、信号增强、噪声抑制、数据压缩以及各种变换、分类判决等。
模式识别是人工神经网络特别适宜求解的一类问题,神经网络模式识别技术在各领域中的广泛应用是神经网络技术发展的一个重要侧面。
(2)人工智能
专家系统是人工智能领域研究时间最长、应用最成功的技术之一。但人们在应用专家系统解决语音识别、图像处理和机器人控制等类似人脑形象思维的问题时却遇到很大的困难。
神经网络的问世为人工智能开辟了一条崭新的途径,它具有自学习能力和较好的容错能力,可以有效进行预测和估计,主要应用在语言处理、市场分析、预测估值、系统诊断、事故检查、密码破译、语言翻译、逻辑推理、知识表达、智能机器人和模糊评判等。
(3)控制工程
神经网络在诸如机器人运动控制、工业生产中的过程控制等复杂控制问题方面有独到之处,较之基于传统数字计算机的离散控制方式、神经网络更适宜于组成快速实时自适应控制系统。
这方面的主要应用有:多变量自适应控制,变结构优化控制,并行分布控制,智能及鲁棒控制等。
(4)优化计算和联想记忆
由于并行和分布式的计算结构,神经网络在求解诸如组合优化、非线性优化等一系列问题上表现出高速的集体计算能力,在VLSI自动排版、高速通信开关控制、航班分配、货物调度、路径选择、组合编码排序、系统规划、交通管理以及图论中各类问题的计算等方面得到了成功应用。
联想记忆的作用是用一个不完整或模糊的信息联想出存储在记忆中的某个完整、清晰的模式来。如何提高模式存储量和联想质量仍是神经网络的热点之一,目前在这方面的应
用有内容寻址器、人脸识别器、知识数据库等。
(5)信号处理
神经网络的自学习和自适应能力使其成为对各类信号进行多用途加工处理的一种天然工具。主要用于解决信号处理中的自适应和非线性问题,包括自适应均衡、自适应滤波、回波抵消、自适应波束形成、自适应编码等自适应问题和各种非线性问题。如非线性区域的模式分类、系统辨识和高维非线性系统的检测估计等问题,还可对病态问题进行求解
神经网络在弱信号检测、通信、自适应滤波等方面的应用尤其引人注目,并已在许多行业得到应用。
四、遗传算法
1. 遗传算法的优点
① 全局性:遗传算法在搜索过程中不易陷入局部极值点,即使在非连续和含有噪声的情况下,也能以较大概率收敛到最优解或满意解,具有很强的容噪能力。
② 并行性和高效性:遗传算法具有大范围全局搜索和并行性等特点,适用于并行计算,因而执行效率高。
③ 鲁棒性:鲁棒性强意味着遗传算法的搜索以群体为基本单元,不受初始选择的影响,不因实例的不同而蜕变;同时对于一个相同问题,在不同的多次运行中能够得到相同结果,在解的质量上没有很大差异。这已被许多数值所证实。
④ 普适性和易扩性:遗传算法是一种弱方法,它采用自然进化机制来表示复杂现象,对函数的形态无要求,可解决多种优化搜索问题。针对不同实例,只需适当调整算子参数等,进行很小修改即可适应新的问题,程序能够通用,这是现行的其他大多数优化方法所做不到的。
⑤ 简明性:遗传算法的基本思想简单明了,实现步骤通俗易懂。
2. 基本原理
遗传算法是从代表问题可能解集的一个种群(popula-tion)开始的,而种群则是由经过基因(gene)编码的一定数目的个体(individual)所组成。每个个体实际上是染色体(chromosome)带有特征的实体。染色体作为遗传物质的主要载体,即多个基因的集合,其内部表现(即基因型)是某种基因组合,它决定了个体的形状的外部表现。
因此,首先要进行编码,实现从表现型到基因型的映射。然后在初代种群产生后,按照适者生存和优胜劣汰的原理,逐代(generation)演化产生出越来越好的近似解。
在每一代,根据问题域中个体的适应度(fitness)大小选择个体,并借助自然遗传学的遗传算子(genetic operators)进行交叉(crossover)和变异(mutation),产生代表新解集的种群。这个过程将导致种群像自然进化一样,后代种群比前代更加适应于环境,末代种群中的最优个体经过解码(decoding),可以作为问题的近似最优解。
遗传算法的实现包括参数编码(编码的任务就是将问题空间的参数转换成遗传空间的、由基因按一定结构组成的染色体或个体)、初始群体的设定、 适应度函数的设计、遗传操作设计(选择、交叉和变异)和控制参数设定(包括交叉概率和变异概率)五个方面。
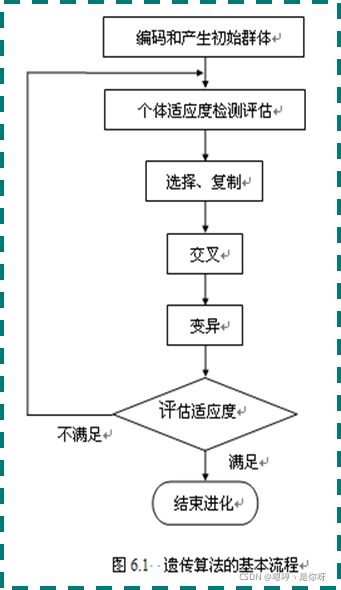
3. 流程
① 产生初始群体,随机地(通常均匀地)产生个个体,每个个体看作是一个染色体,个染色体组成一个群体;
② 对群体中每个个体计算它的适应度值;
③ 通过选择和复制操作从群体中选出所需个体,并放入到交配缓冲池中;
④ 对交配池中的个体使用交叉和变异算子形成下一代群体中的个个体,并计算每个新个体的适应度值;
⑤ 如果满足结束条件,则停止;否则转到第③步。
4. 应用
遗传算法可应用于函数优化、组合优化、生产调度、自动控制、机器人学习、图像处理、人工生命等方面。
四、蚁群算法
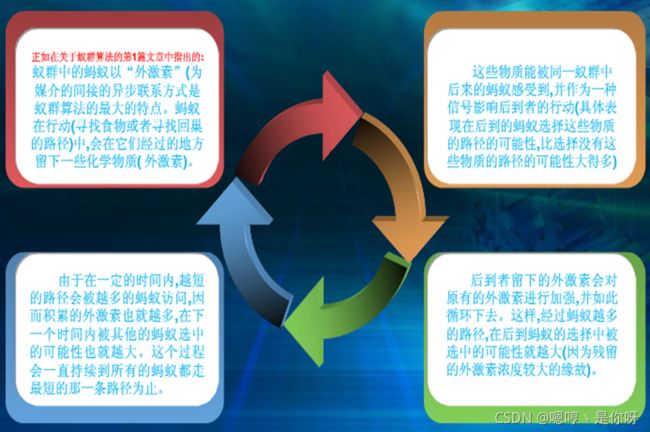
1. 蚁群算法的特点
① 蚁群算法是一种自组织算法。在算法初期,单个蚂蚁无序地寻找解,经过一段时间后蚂蚁通过信息激素,自发地趋向到寻找到接近最优解的一些解,这是一个无序到有序的过程。
② 蚁群算法本质上是一种并行算法。每只蚂蚁搜索的过程彼此独立,仅通过信息激素进行通信。
③ 蚁群算法是一种正反馈算法。蚂蚁能够最终找到最短路径,直接依赖于最短路径上信息激素的堆积,而信息激素的堆积却是一个正反馈过程。
④ 蚁群算法具有较强的鲁棒性。相对于其它算法,蚁群算法对初始路线要求不高,即蚁群算法的求解结果不依赖于初始路线的选择,而且在搜索过程中不需要进行人工调整。其次,参数数目少,设置简单,易于应用到其它组合优化问题的求解中。
⑤ 蚁群算法不依赖于所求问题的具体数学表达式,具有很强的找到全局最优解的优化能力。
⑥ 蚁群算法的成功主要在实验层次,缺乏坚实的数学基础和数学解释。
⑦ 蚁群算法的局部搜索能力较弱,易出现停止和局部收敛、收敛速度慢等问题。
2. 蚁群算法的基本描述
① 预先初始化各边信息素强度及各蚂蚁的禁忌表。各蚂蚁按照一定的概率规则,在禁忌表的制约下选择下一个要到达的节点,直至最终形成一条合法的路径。
② 计算各蚂蚁产生的路径长度,路径长度是路径中各边长度之和。
③ 更新各边的信息素。各边先进行信息素挥发操作,然后根据各蚂蚁产生的路径长度获取蚂蚁所释放的信息素。
④ 当所有蚂蚁均完成了信息素的更新操作后,记录当前的最短路径,并且对禁忌表及进行初始化,并转到步骤②。依次循环下去,直到满足算法的终止条件为止。
3. 蚁群算法的应用