【学习笔记】：PointNet的补充材料

1.比较PointNet与VoxNet的网络：

使用两个网络处理缺失点云数据，测试鲁棒性，划分相同的数据集，以1024个点作为输入。对于VoxNet，将点云数据划为323232的网格，并使用随即旋转与抖动增强数据集。由于VoxNet对旋转敏感，使用十二个视点的平均分数，结果如下：

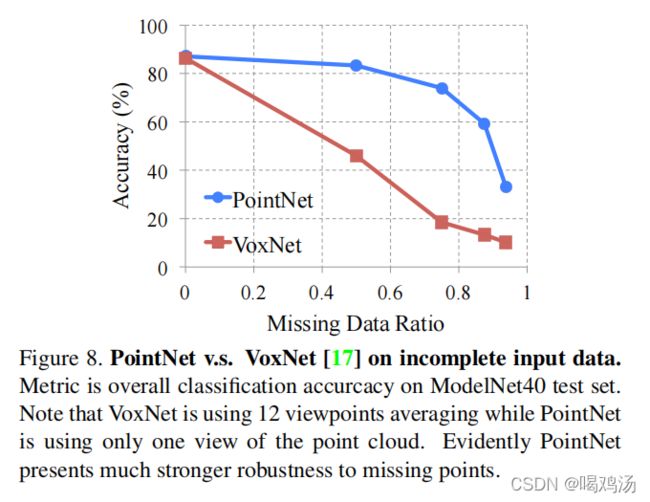
本文提出的网络对于数据缺失具有较强的鲁棒性。

2.网络框架和训练细节：

a.点云分类网络：

mini-PointNet（输入变换和特征变换），输入原始点云数据得到一个$3\ast 3$的矩阵，该网络又权值共享的MLP、最大池化和两个全连接层组成。 输出将矩阵倍初始化为一个单位矩阵。 除了最后一层都使用ReLu激活和批归一化处理。特征变换网络与上一个框架相同只不过输出64*64的矩阵。
在softmax分类器中加入正则化损失（权重0.001）实矩阵接近正交，在最后一个全连接层上使用0.7的dropout，并输出256个维度。批归一化的衰减率从0.5开始，然后逐渐增加到0.99。

b.点云分割网络：

分割网络使分类网络的延申，将分类网络的全局特征（softmax得到的）与中间层得到的局部特征（特征变换得到的）拼接，分割网络不使用Dropout，使用分类网络训练的参数。在拼接时又加入了表示输入类的独热编码向量（长为16）。

交叉类别进行训练（使用独热编码进行表明类别），只预测给定对象类别的部件标签。

c.三维卷积语义分割对照网络（Baseline 3D CNN Segmentation Network）：

对于给定的点云数据先将其转换为32×32×32的立方体网格，第一层使用5个三维卷积核进行卷积，每层有32个通道，前四层为$5\ast 5\ast 5$的核最后一层使用$3\ast 3\ast 3$（会不断缩小最后输出$18\ast 18\ast 18$大小）。每个体素的接受域为19 ，在计算出的特征图上添加$1\ast 1\ast 1$的三维卷积层序列用来预测每个体素的分割标签。本网络是进行跨类别训练（但是会有标签信息）的，为了与其他方法对比，只考虑给定对象类别的输出分数。

3.检测方案的细节：

基于语义分割和分类设计三维目标检测系统，通过带有分割分数的连通分量获取场景中的目标信息，从场景中的随即一点开始，预测标签并且使用BFS收缩具有相同标签的点，收缩半径为0.2米。得到的结果簇如果超过200个点（如果结果少于200个点会减去），判定簇的边界框为一个对象，每一个预测对象的检测分数为该类别的平均分数。如果一个场景中有多个相同物体彼此相连，不能正确的将他们划分开（采用分类网络和滑动形状分割缓解这类问题）。
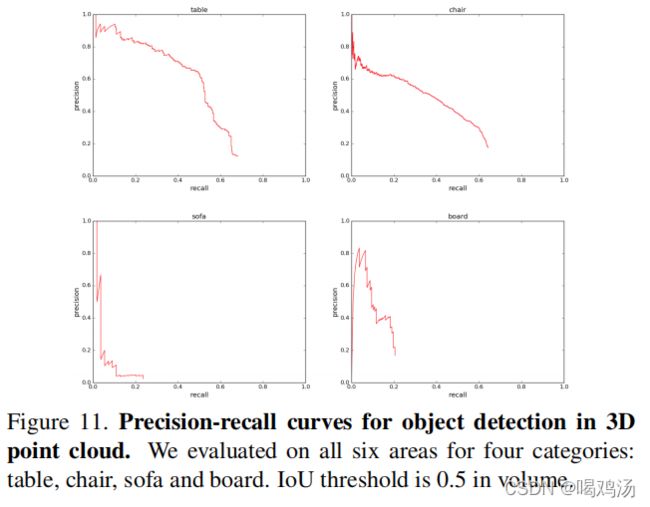
为每个类别训练一个二元分类网络，并采用滑动窗口检测，另外使用非最大抑制修剪，将联通分量与滑动形状预测边界组合进行最终评估。作者训练了六个模型，每个模型都在五个区域进行训练，并在左侧区域测试（左侧区域未参与训练），所有六个区域结果构成PR（召回）曲线：

4.更多应用：

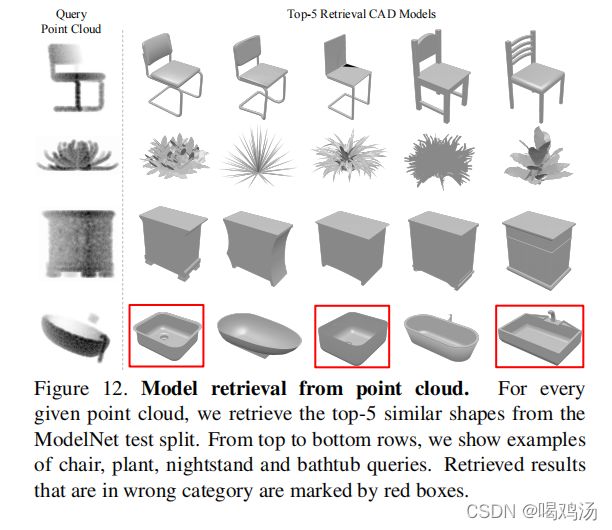
从点云中检索模型：本模型学习全局的特征，作者希望几何上相似的形状具有相似的全局特征，于是对于给定的查询形状，输入网络获取全局特征（在得分层之前输出），并且使用最邻近方法检索类似的形状。结果如下：其中红色框选的是错误检索的。

形状关系：本网络获得的特征可以用于计算形状之间的对应关系，输入两个形状，匹配全局特征的相同维度来计算关键点之间的对应关系。

5.结构分析：

最大池化的维度和输入点数的影响：

比较了最大层输出的大小和输入的点数对性能的影响，随着最大池化的输出增大准确率得到提升，在1K左右达到峰值，提升了3%左右的准确率。表明需要足够的点特征函数覆盖三维空间以区分不同的形状。

MNIST数字分类：

将网络拓展到二维的MNIST（手写数字）点云数据集，作者设置阈值并且添加了像素值大于128的像素，设置点集个数为256，若多于进行采样，少于进行填充。作者与其他传统的框架进行对比，结果好于其他的框架。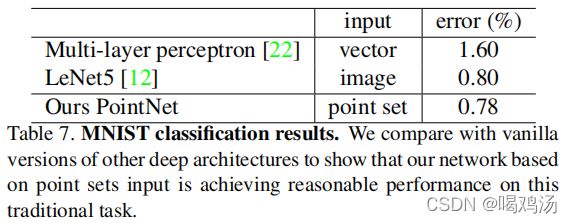

法线估计：

作者进行了全局与局部特征拼接，为局部提供了上下文信息，对拼接是否提供了上下文信息进行了探索，作者验证了分割网络可以预测点的法向量，也就验证了可以提供局部的上下文信息。设置有了一个有监督的版本，改变最后一层获得预测的法向量，并将余弦距离的绝对值作为损失。作者认为得到的结果在一些局部位置比金标准还光滑。

分割鲁棒性：

如上文所讲，分类网络对数据缺失和噪声具有较强的鲁棒性，这里讨论风格网络的鲁棒性。每点的预测值是基于每点的特征和全局特征得到的，结果如下，左图为输入，中间为关键点，右边为预测的最大可能边界，分割结果基本与关键点一致，

网络对不可见类别的实验：

就是测试网络对没有经过训练点集的识别能力，作者分析新出现的类别中对了一些网络未学到的平面信息，所以还是有些欠缺，但整体效果还是理想的。

6.定理论证：

定理一论证了设计的网络式一个对称的网络，并且可以拟合任意一个连续函数。

定理一：由于f是连续函数，取${\delta }_{ϵ}$,当$d_H(S,S^{\prime })<{\delta }_{ϵ}$时，对任意$S,S^{\prime }\in \mathcal{X}$都有$|f(S)-f(S^{\prime })|<ϵ$ 。取$K=[1/{\delta }_{ϵ}]$，将[0,1]划分为K个空间，并定义一个辅助函数将点映射到区间的左端，（中括号表示取整函数）$$令，S=\delta (x)=\frac{[K_x]}{K},x\in S$$
则$$d_H(S,S^{\prime })<1/K\le {\delta }_{ϵ}(我认为这里直接取等号就行)$$且，$$|f(S)-f(S^{\prime })|<ϵ$$设指数函数$h_k(x)=e^{-d(x,[\frac{k-1}{K},\frac{k}{K}])}$，其中$d(x,I)$表示要设定间隔的距离（我认为是输入点云数据到K个区间的每个单独的距离，也就是分别计算每点到每个类别的距离），$$\mathbf{h}(x)=[h_1(x),...h_K(x)]，将h由\mathbb{R}映射到{\mathbb{R}}^K$$
设$$v_j(x_1,...x_n)=max\{h_j(x_1),...,h_j(x_n)\}$$ 用S中的点表示第j个区间的占用率。$$\mathbf{v}=[v_i;...;v_K]，即将\mathbf{v}由{\mathbb{R}}^n映射到\{0,1{\}}^K$$
表示将输入的n个点转换为K个空间的最大可能值，每个点最大的可能值（或者可以理解为特征值），{0，1}的话可能类似与独热编码，若某个位置最大取值为1，不是最大标记为零。这是一个对称函数（不因输入序列的变化而改变结果），表示每个区间在S中的占用点（每个点所属的区间）。
定义$\tau$为$\{0,1{\}}^K到\mathcal{X}$的映射，即$$\tau (v)=\{\frac{k-1}{K},v_k\ge 1\}（后边的限制应该表示从第一个区间最大值开始）$$
它将占用向量$\mathbf{v}$映射到一个包含每个被占用区间的左端的集合。即：
$$\tau (\mathbf{v}(x_1,...,x_n))\equiv S$$其中，$x_1,...,x_n$是S中元素按一定顺序排列的结果。
又设$\gamma$为${\mathbb{R}}^K$到$\mathbb{R}$的映射，是一个连续函数，定义为：$\gamma (\mathbf{v})=f(\tau (\mathbf{v}));v\in \{0,1{\}}^K$，这样可以将上式修改为：$$|\gamma (\mathbf{v}(x_1,...,x_n))-f(S)|=|f(\tau (\mathbf{v}(x_1,...,x_n)))-f(S)|<ϵ$$
其中，$\gamma (\mathbf{v}(x_1,...,x_n))$可以改写为下式，$$\gamma (\mathbf{v}(x_1,...,x_n))=\gamma (MAX(h(x_1),...,h(x_n)))=(\gamma \circ MAX)(h(x_1),...,h(x_n))$$
其中，$\gamma \circ MAX$为对称函数。

定理二验证了神经网络具有较强的鲁棒性，可以忽略输入数据的干扰。

${\mathcal{C}}_{\mathcal{S}}$为关键点，f(S)为全局特征，${\mathcal{N}}_{\mathcal{S}}$式预测的最大可能形状值，T我认为i是输入的全部点集。显然$f(S)$是由$\mathbf{u}(S)$决定，故只需验证$$\forall S,\exists {\mathcal{C}}_{\mathcal{S}},{\mathcal{N}}_{\mathcal{S}}\in \mathcal{X},f(T)=f(S)\dots \dots 当{\mathcal{C}}_{\mathcal{S}}\in T\in {\mathcal{N}}_{\mathcal{S}}$$对于$\mathbf{u}$的第j维至少存在一个$x_j\in \mathcal{X}$即，$h_j(x_j)={\mathbf{u}}_j$,$h_j$是h向量输出的第j个维数，取${\mathcal{C}}_{\mathcal{S}}$作为j=1，…K的所有$x_j$的并集，则${\mathcal{C}}_{\mathcal{S}}$满足上述条件。
所以，添加一些$h(x)\le \mathbf{u}(S)$不会改变u和f的取值。将这类点叠加到${\mathcal{C}}_{\mathcal{S}}$上就得到了${\mathcal{T}}_{\mathcal{S}}$.