支持向量机SVM学习——多项式核函数、RBF核函数

目录

一、多项式核函数

二、高斯核函数

1、RBF核函数

2、RBF核函数中gamma

三、SVM解决回归问题

---

一、多项式核函数

---

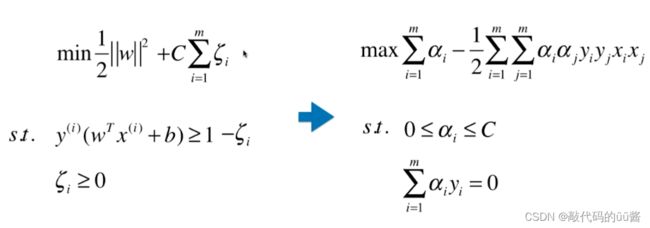
回顾上一小节的SVM算法原理可知，就是求解  的最优解，现在将这个式子转换为     。

然后设置一个函数K，传入两个参数    ，能够直接对原来的两个样本数学运算计算出多项式特征   ，那么最后式子可以表示为 ： 

K函数的作用是省略变形这一步骤，直接将参数带入计算出  点乘的结果，这个K函数也被称为核函数（Kernel Function）。

现将该多项式核函数的设为   ，其推导如下：

因此，多项式核函数定义为   

线性核函数定义为 

代码示例：

import numpy as np
import matplotlib.pyplot as plt

from sklearn import datasets

#自动生成非线性数据集
X, y = datasets.make_moons(noise=0.15, random_state=666) #标准差0.15

from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline

from sklearn.svm import SVC

def PolynomialKernelSVC(degree, C=1.0):
    return Pipeline([
        ("std_scaler", StandardScaler()),
        ("kernelSVC", SVC(kernel="poly", degree=degree, C=C))  
         #kernel="poly"可以达到SVM多项式特征效果
    ])

poly_kernel_svc = PolynomialKernelSVC(degree=3)
poly_kernel_svc.fit(X, y)


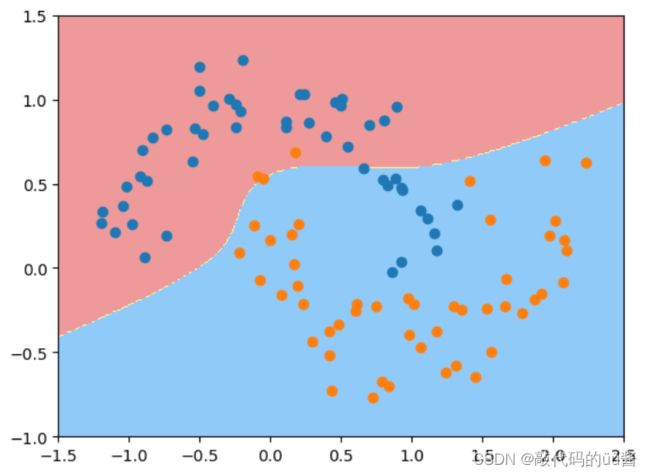
plot_decision_boundary(poly_kernel_svc, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()

运行结果：

二、高斯核函数

---

1、RBF核函数

高斯函数是     ，那么在高斯核函数中  被  给替代了，即  。高斯核函数将每一个样本点映射到一个无穷维的特征空间，它依靠升维使原来线性不可分的数据线性可分。

代码示例：

import numpy as np
import matplotlib.pyplot as plt

#构造线性不可分数据
x = np.arange(-4, 5, 1)
y = np.array((x >= -2) & (x <= 2), dtype='int')

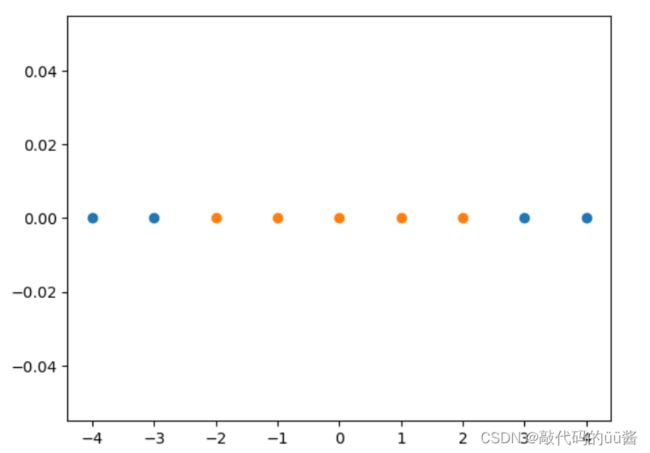
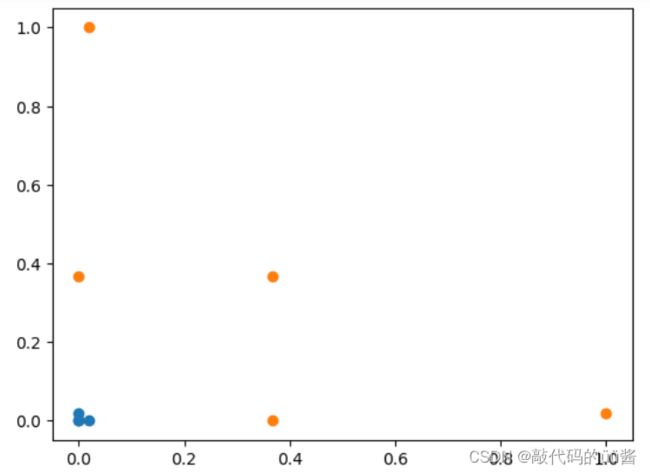
plt.scatter(x[y==0], [0]*len(x[y==0]))
plt.scatter(x[y==1], [0]*len(x[y==1]))
plt.show()

#构造高斯核函数
def gaussian(x, l):
    gamma = 1.0
    return np.exp(-gamma * (x-l)**2)

#映射
l1, l2 = -1, 1

X_new = np.empty((len(x), 2))
for i, data in enumerate(x):
    X_new[i, 0] = gaussian(data, l1)
    X_new[i, 1] = gaussian(data, l2)
    
plt.scatter(X_new[y==0,0], X_new[y==0,1])
plt.scatter(X_new[y==1,0], X_new[y==1,1])
plt.show()

运行结果：

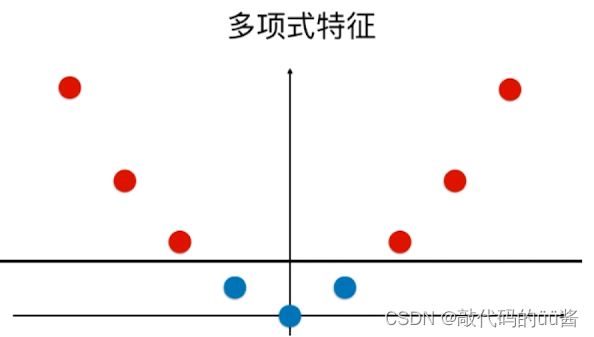
最终我们将一个一维线性不可分数据映射为二维线性可分数据。

2、RBF核函数中gamma

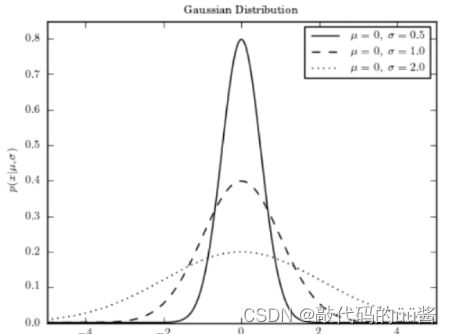
高斯函数是   中  和  的分布情况如下，对应高斯核函数   中 gamma越大，高斯分布越窄；gamma越小，高斯分布越宽。

代码示例：

import numpy as np
import matplotlib.pyplot as plt

from sklearn import datasets

#随机样本
X, y = datasets.make_moons(noise=0.15, random_state=666)

from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.svm import SVC

#管道
def RBFKernelSVC(gamma):
    return Pipeline([
        ("std_scaler", StandardScaler()),
        ("svc", SVC(kernel="rbf", gamma=gamma))
    ])

svc = RBFKernelSVC(gamma=10)  #gamma取值不同，决策效果也不同
#svc = RBFKernelSVC(gamma=1)
#svc = RBFKernelSVC(gamma=100)
svc.fit(X, y)

#绘制决策边界
def plot_decision_boundary(model, axis):
    
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1, 1),
    )
    X_new = np.c_[x0.ravel(), x1.ravel()]

    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)

    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    
    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)

plot_decision_boundary(svc, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()

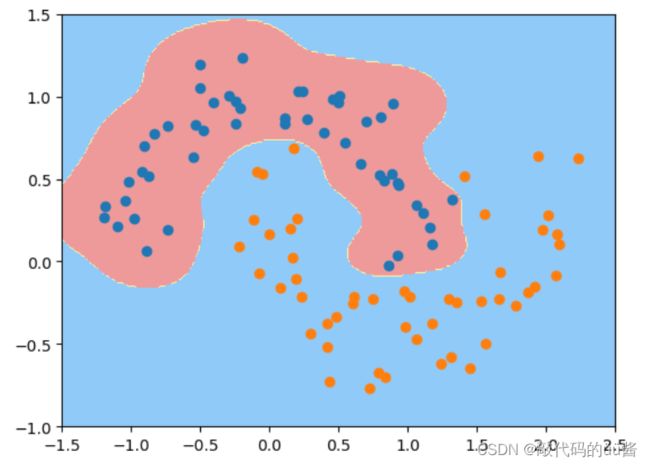
运行结果：

 

根据决策边界图我们调整gamma的值来让模型达到最优的效果。gamma越小，模型复杂度越低，越倾向欠拟合；gamma越大，模型复杂度越高，越倾向过拟合。

三、SVM解决回归问题

---

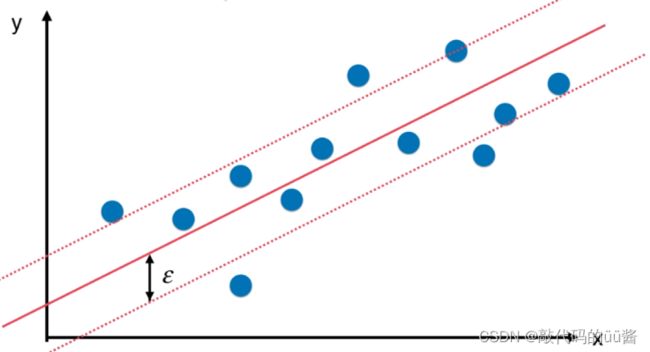
利用SVM解决回归问题时，我们在决策边界距离引入一个指定的超参数  ，旨在让决策边界内的样本尽可能多。

 

#波士顿房产数据集
boston = datasets.load_boston()
X = boston.data
y = boston.target

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)

from sklearn.svm import LinearSVR
from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline

def StandardLinearSVR(epsilon=0.1):
    return Pipeline([
        ('std_scaler', StandardScaler()),
        ('linearSVR', LinearSVR(epsilon=epsilon))
    ])

svr = StandardLinearSVR()
svr.fit(X_train, y_train)

svr.score(X_test, y_test)