1143. Longest Common Subsequence 1035. Uncrossed Lines 53. Maximum Subarray
1143. Longest Common Subsequence
Given two strings text1 and text2, return the length of their longest common subsequence. If there is no common subsequence, return 0.
A subsequence of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
- For example,
"ace"is a subsequence of"abcde".
A common subsequence of two strings is a subsequence that is common to both strings.
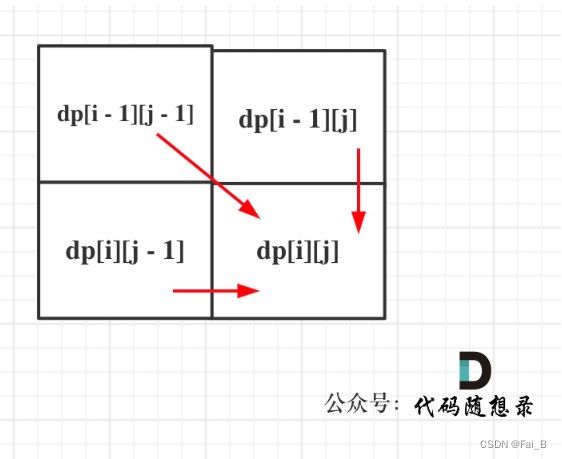
There are two main cases to determine the recursive formula:
1. text1[i - 1] is the same as text2[j - 1]
2. text1[i - 1] is not the same as text2[j - 1].
If text1[i - 1] and text2[j - 1] are the same, then a common element is found, so dp[i][j] = dp[i - 1][j - 1] + 1;
If text1[i - 1] and text2[j - 1] are not the same, then look at the longest common subsequence of text1[0, i - 2] and text2[0, j - 1] and the longest common subsequence of text1[0, i - 1] and text2[0, j - 2] and take the largest. i.e., dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
2-dimensional DP:
Time complexity: O(m x n)
Space complexity: O(m x n)
class Solution:
def longestCommonSubsequence(self, text1: str, text2: str) -> int:
# 创建一个二维数组 dp,用于存储最长公共子序列的长度
dp = [[0] * (len(text2) + 1) for _ in range(len(text1) + 1)]
# 遍历 text1 和 text2,填充 dp 数组
for i in range(1, len(text1) + 1):
for j in range(1, len(text2) + 1):
if text1[i - 1] == text2[j - 1]:
# 如果 text1[i-1] 和 text2[j-1] 相等,则当前位置的最长公共子序列长度为左上角位置的值加一
dp[i][j] = dp[i - 1][j - 1] + 1
else:
# 如果 text1[i-1] 和 text2[j-1] 不相等,则当前位置的最长公共子序列长度为上方或左方的较大值
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
# 返回最长公共子序列的长度
return dp[len(text1)][len(text2)]
1-dimensional DP:
Time complexity: O(m x n)
Space complexity: O(m)
class Solution:
def longestCommonSubsequence(self, text1: str, text2: str) -> int:
m, n = len(text1), len(text2)
dp = [0] * (n + 1) # 初始化一维DP数组
for i in range(1, m + 1):
prev = 0 # 保存上一个位置的最长公共子序列长度
for j in range(1, n + 1):
curr = dp[j] # 保存当前位置的最长公共子序列长度
if text1[i - 1] == text2[j - 1]:
# 如果当前字符相等,则最长公共子序列长度加一
dp[j] = prev + 1
else:
# 如果当前字符不相等,则选择保留前一个位置的最长公共子序列长度中的较大值
dp[j] = max(dp[j], dp[j - 1])
prev = curr # 更新上一个位置的最长公共子序列长度
return dp[n] # 返回最后一个位置的最长公共子序列长度作为结果
1035. Uncrossed Lines
You are given two integer arrays nums1 and nums2. We write the integers of nums1 and nums2 (in the order they are given) on two separate horizontal lines.
We may draw connecting lines: a straight line connecting two numbers nums1[i] and nums2[j] such that:
nums1[i] == nums2[j], and- the line we draw does not intersect any other connecting (non-horizontal) line.
Note that a connecting line cannot intersect even at the endpoints (i.e., each number can only belong to one connecting line).
Return the maximum number of connecting lines we can draw in this way.
Its literaly like to get longest common subsequence from "adb" and "abd"
It's exactly the same as the last question.
class Solution:
def maxUncrossedLines(self, nums1: List[int], nums2: List[int]) -> int:
m = len(nums1)
n = len(nums2)
dp = [[0] * (n + 1) for _ in range(m + 1)]
for i in range(1, m + 1):
for j in range(1, n + 1):
if nums1[i - 1] == nums2[j - 1]:
dp[i][j] = dp[i - 1][j - 1] + 1
else:
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
return dp[-1][-1]
53. Maximum Subarray
Given an integer array nums, find the subarray with the largest sum, and return its sum.
第二次还没ac 老了老了
dp:
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
dp = [float('-inf')] * len(nums) # 不能 -inf
dp[0] = nums[0]
result = dp[0] #初始化 ,必须要有 ,不能直接max(dp)
for i in range(1, len(nums)):
dp[i] = max(nums[i], dp[i - 1] + nums[i]) # 不是dp[i]是num[i] !!!!!!!!!!
if dp[i] > result:
result = dp[i]
return result