用K近邻（KNN）机器学习算法进行股票走势预测-Python

什么是K近邻（KNN）

K近邻(KNN，K-Nearest Neighbors)是最简单的机器学习算法之一，可用于回归和分类。KNN是一种“惰性”学习算法，从技术上讲，它不训练模型来进行预测。K近邻的逻辑是，假设有一个观测值，这个观测值被预测属于离它k个最近观测值中所占比例最大的那一个类。KNN方法是直接尝试使用实际数据来近似条件期望。

对于回归，预测值是K个邻居的均值，估计量（estimator）为
$$\hat{f}(x)=Average[y_i|x_i\in N_k(x)]$$
$N_k(x)$是x的 包含k个 最靠近的 观测值的 邻域。

对于分类，所预测的标签是具有“多票者胜”性质的类，即，哪个类在相邻类中最具代表性。这相当于在k个最近的邻居中进行多数投票。对于每一类j = 1，…， K，然后我们计算条件概率
$$\mathrm{Pr}(G=j|X=x_0)=\frac{1}{k}\sum _{i\in N_k(x)}I(y_i=j)$$
把观察值归类给条件概率最高的那一类。这里的$I(y_i=j)$是指示函数，如果$y_i=j$输出$1$，否则输出$0$。

KNN的“三步走”过程

KNN之所以受欢迎，是因为它很容易理解和被解释。它的准确性一般与更复杂的算法相当，甚至更好。一旦k被指定，找到最近的邻居是一个三步的过程。

步骤	备注
第1步	计算距离，通常是欧几里得距离
第2步	按距离升序排序，找到k个最近邻
第3步	计算KNN观测值的平均值或概率

寻找邻居

比如说，我们有一个二维的直角坐标，横轴和纵轴分别代表两个不同的特性。现在所有的反映这两个特性的数据点已经在坐标系中标好。
直觉上，距离可以被认为是相似性的度量。直白点说，就是在这个坐标系中，两个点距离越接近，这两个点代表的特征就越相似。
欧几里得距离（Euclidean distance）是最常用的，但其他距离度量如曼哈顿（Manhattan distance）也可以。广义距离度量称为闵可夫斯基距离（Minkowski distance），定义为
$$d=(\sum _{n=1}^n|x_i-y_i{|}^p{)}^{\frac{1}{p}}$$
其中$x_i$和$y_i$是用超参数(hyperparameter，即整数 $p$)计算距离$d$的两个观测值。

当 $p=1$ 时，闵可夫斯基距离是曼哈顿距离，当 $p=2$ 时，闵可夫斯基距离只是标准欧几里得距离。使用距离度量识别出K个邻居后，该算法可以使用邻居的标签值进行分类或预测。

KNN模型

KNN是一种非参数方法，它不假设任何函数，因为没有参数需要估计。邻居个数，也就是k的选择是使用训练集完成的。选择接近1的k具有最大的灵活性(低偏差)，但也具有最高的可变性(高方差)，而另一方面，选择较大的k具有最大的灵活性(高偏差)，但也具有最低的可变性(低方差)。要注意，当 $k=N$ 时，将把所有新的测试观察值分配给单个类。选择k的最佳方法是通过交叉验证（cross validation），这个我们后面再展开。另一种替代方法是使用Elbow method来选择k。

案例概述

接下来我们来进行KNN算法的实战操作。目标是，我们将利用KNN预测市场走向，并在此基础上制定交易策略。这里我们只简单用SPY的数据。

导入库

老规矩，先导入我们这个项目需要的库。

# Base libraries
import pandas as pd
import numpy as np

# Plotting
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (12,8)
plt.style.use('fivethirtyeight')

# Preprocessing
from sklearn.preprocessing import MinMaxScaler
from sklearn.pipeline import Pipeline
from sklearn.model_selection import train_test_split, GridSearchCV, TimeSeriesSplit

# Classifier
from sklearn.neighbors import KNeighborsClassifier

# Metrics
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix
from sklearn.metrics import plot_confusion_matrix, auc, roc_curve, plot_roc_curve

# Ignore warnings
import warnings
warnings.filterwarnings('ignore')

检索数据

数据来源：yfinance，SPY，20001.1-2023.4.5

# Load locally stored data
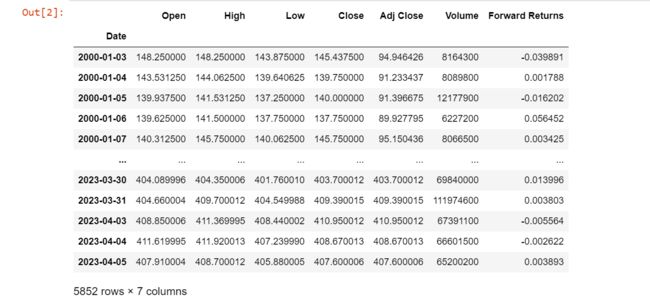
df = pd.read_csv('./SPY.csv', index_col=0, parse_dates=True)
# log相减（取差分）
df['Forward Returns'] = np.log(df['Adj Close']).diff().shift(-1)

# Check first 5 values
df = df.dropna()
df

# Check for missing values
df.isnull().sum()

特征工程

特征在这里是自变量，用来确定目标变量的值。我们将从原始数据集创建特征和目标(标签)。

目标或标签定义

标签或目标变量（target variable）是因变量。在这里，目标变量是识别SPY在下一个交易日收盘时是涨还是跌。如果明天的收益大于远期收益的中位数，我们将买入SPY，否则我们将卖出SPY。

我们为目标变量的买入信号赋值+1，为卖出信号赋值-1。目标可以描述为:

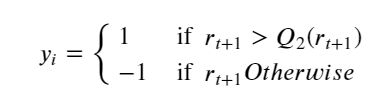
其中$Q_2(r_{t+1})$为SPY下一天收益的中位数（第二个四分位数）。

之所以选择用中位数，而不使用0作为目标变量的分界线，是因为很难使用特别接近0的回报作为股票即将上涨或下跌的信号。如果将0作为股票涨跌的信号，原始数据的分布或者+1或-1的分布都不是很均匀，会使分类器的效果变差。

回观之前的数据，我们已经有了SPY的开盘价、收盘价等。这些指标（Predictors）直接用也能用，但是我们先建两个技术指标，作为特征值进行预测，代码如下。

# Predictors 
df['O-C'] = df.Open - df.Close
df['H-L'] = df.High - df.Low

# X是合成的工具，变为数组
X = df[['O-C','H-L']].values
X[:5]

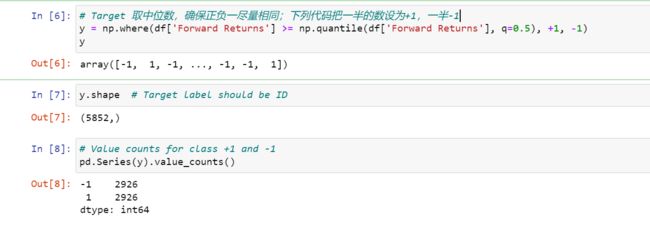
目标变量取中位数，确保正负一尽量相同；下列代码把一半的数设为+1，一半-1。

# Target 
y = np.where(df['Forward Returns'] >= np.quantile(df['Forward Returns'], q=0.5), +1, -1)
y

y.shape  # Target label should be ID

# Value counts for class +1 and -1
pd.Series(y).value_counts()

输出结果如下。

将数据集分成训练和测试数据

# Splitting the datasets into training anf testing data
# Always keep shuffle = Fales for financial time series
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, shuffle=False)

# Output of the train and test data size
print(f"Train and Test size {len(X_train),len(X_test)}")

拟合模型

由于KNN模型计算距离，因此需要对数据集进行缩放才能使模型正常工作。所有的特征都应该有相似的尺度。关于数据缩放和尺度的详细内容和示例可以看我的第一篇博客（金融数据的预处理）。缩放可以通过使用“MinMaxScaler”转换器来完成。

# Scale and fit the model
pipe = Pipeline([
    ("scaler", MinMaxScaler()),
    ("classifier", KNeighborsClassifier())
])

pipe.fit(X_train, y_train)

# Target Classes
class_names = pipe.classes_
class_names

预测和概率

# Predicting the test dataset
y_pred = pipe.predict(X_test)

acc_train = accuracy_score(y_train, pipe.predict(X_train))
acc_test = accuracy_score(y_test, y_pred)

print(f"Train accuracy: {acc_train:0.4}, Test accuracy: {acc_test:0.4}")

我得到的结果是这样的

# predict probabilities
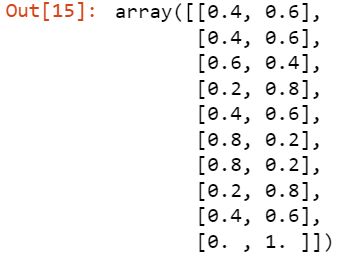
probs = pipe.predict_proba(X_test)
probs[:10]

# predict y
y_pred[:10]

预测质量

混淆矩阵

混淆矩阵是一种用于评估分类模型或算法预测质量的工具，它能够展示模型在不同类别上的预测结果与真实标签之间的对应关系。通过混淆矩阵，我们可以计算出各种评估指标，如准确率、召回率、精确率和F1分数等，来评估模型的性能。

下面是一个二分类问题的混淆矩阵示例：

                      预测结果
                     正例  负例
真实值           正例  TP   FN
                 负例  FP   TN

在混淆矩阵中，有四个关键术语：

• 真正例（True Positive，TP）：模型正确预测为正例的样本数。
• 假负例（False Negative，FN）：模型错误预测为负例的样本数。
• 假正例（False Positive，FP）：模型错误预测为正例的样本数。
• 真负例（True Negative，TN）：模型正确预测为负例的样本数。

通过这些值，我们可以计算以下评估指标：

1. 准确率（Accuracy）：表示模型预测正确的样本数与总样本数之比，计算公式为 (TP + TN) / (TP + TN + FP + FN)。

2. 召回率（Recall）：表示模型能够正确预测出的正例样本数与真实正例样本数之比，计算公式为 TP / (TP + FN)。

3. 精确率（Precision）：表示模型预测为正例的样本中真正为正例的比例，计算公式为 TP / (TP + FP)。

4. F1分数（F1 Score）：综合考虑了精确率和召回率，是精确率和召回率的调和平均数，计算公式为 2 * (精确率 * 召回率) / (精确率 + 召回率)。

这些指标可以帮助我们判断模型在不同类别上的预测性能，根据具体问题的要求选择合适的评估指标进行模型的评估。

在混淆矩阵中，"正例"和"负例"是指待分类的两个类别。这些类别的具体含义取决于具体的应用场景和问题。

通常情况下，"正例"代表我们关注的事件或感兴趣的目标，而"负例"则表示其他事件或非目标。例如，在一个垃圾邮件分类问题中，"正例"可以表示垃圾邮件，"负例"表示正常邮件。

“真”和“假”是指该预测是否与外部判断(有时称为“观测”、“真实情况”)相对应。

# Confusion matrix for binary classification
tn, fp, fn, tp = confusion_matrix(y_test, y_pred).ravel()
print(tn, fp, fn, tp)

输出结果为：246 338 258 329

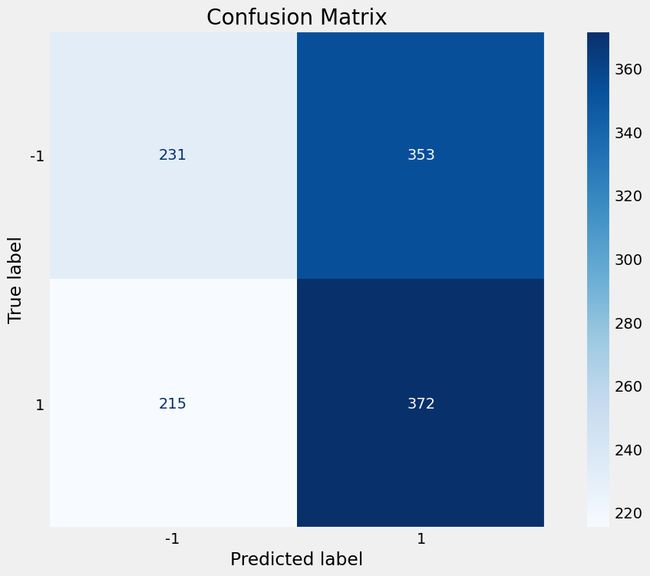
# Plot confusion matrix
plot_confusion_matrix(pipe, X_test, y_test, cmap='Blues', values_format='.4g')
plt.title('Confusion Matrix')
plt.grid(False)

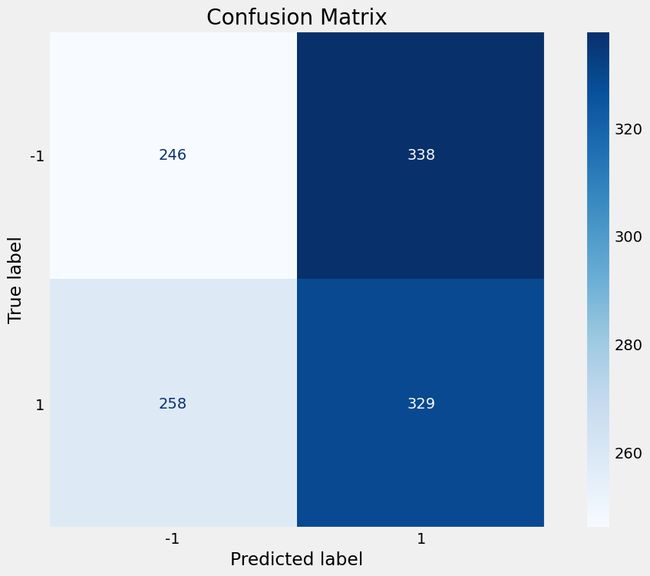
分类报告用于衡量分类算法预测的质量。接下来我们输出分类报告，其中分别计算了准确率等评估指标。

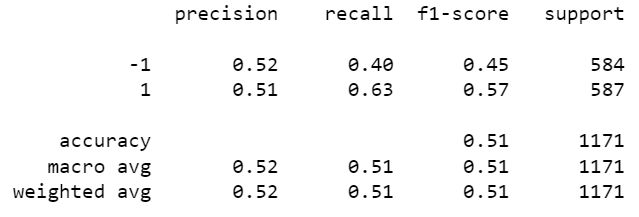
# Classification report
print(classification_report(y_test, y_pred))

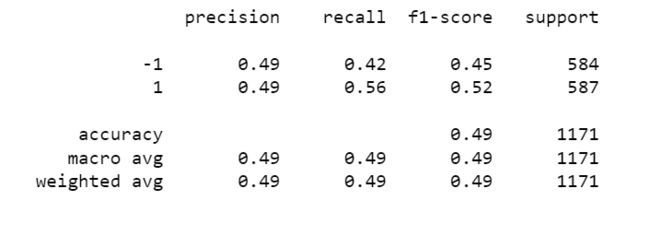
在分类问题的评估报告（classification report）中，除了展示各个类别的指标之外，还会提供宏平均（macro average）和加权平均（weighted average）两种整体评估的指标。这些指标可以帮助我们了解模型在整体上的性能表现。

宏平均（macro average）是计算各个类别指标的平均值，不考虑类别样本数量的差异。具体步骤如下：

1. 对于每个类别，计算该类别的评估指标（如准确率、召回率、精确率、F1分数等）。
2. 对所有类别的评估指标进行平均，得到宏平均值。

宏平均的计算方式简单明了，对每个类别的性能都给予了相等的重视，不受类别样本数量的影响。

加权平均（weighted average）是计算各个类别指标的加权平均，考虑了每个类别样本数量的差异。具体步骤如下：

1. 对于每个类别，计算该类别的评估指标。
2. 根据每个类别的样本数量，计算出相应的权重。
3. 将每个类别的评估指标乘以相应的权重，并进行加权求和。
4. 将加权求和的结果除以所有类别样本总数，得到加权平均值。

加权平均考虑了不同类别的样本数量差异，较大样本数量的类别在计算平均值时具有更大的权重。

宏平均和加权平均都提供了整体性能评估的视角，但是它们对不平衡数据集的处理方式有所不同。在样本数量相对平衡的情况下，两者可能会给出相似的结果，而在样本数量不平衡的情况下，加权平均更倾向于较大类别的性能表现。

选择使用宏平均还是加权平均取决于具体问题和关注的重点。如果各个类别对你来说都是同等重要的，可以使用宏平均。如果你更关注样本数量较多的类别，可以使用加权平均。

指标差不多都是0.5，F1分数甚至出现0.45。模型的预测结果在某些方面并没有明显优势。这可能表明模型的预测能力较为一般，无法有效地区分正例和负例。

ROC曲线下面积

ROC曲线下的面积（Area Under the ROC Curve，AUC）是一种用于衡量二分类模型性能的常用指标。ROC曲线是以不同的分类阈值为基础，绘制出真阳性率（True Positive Rate，TPR，也称为召回率）与假阳性率（False Positive Rate，FPR）之间的关系曲线。

AUC表示ROC曲线下的面积，其取值范围在0到1之间。AUC的含义是模型正确分类的能力：AUC越接近1，表示模型在不同阈值下具有较高的真阳性率，同时较低的假阳性率，即模型具有较好的性能。而AUC越接近0.5，则说明模型的性能越接近于随机分类。

AUC具有以下特点：

1. 不受分类阈值的影响：AUC是综合考虑了不同阈值下的模型表现，因此不受分类阈值的选择影响。

2. 对类别不平衡的数据集友好：AUC对于样本类别不平衡的问题比准确率等指标更加稳定，能够更好地反映出模型在不同类别之间的区分度。

3. 提供了模型排序的能力：AUC可以将模型的性能转化为排序能力，即对于任意一对样本，模型正确排序的概率。

综合来说，AUC是一种常用的评估指标，用于衡量二分类模型的性能。较高的AUC值表示模型具有较好的分类能力，而较低的AUC值可能需要进一步改进模型或考虑其他方法来提高预测性能。

# Random Prediction
r_prob = [0 for _ in range(len(y_test))]
r_fpr, r_tpr, _ = roc_curve(y_test, r_prob, pos_label=1)

# Plot ROC curve
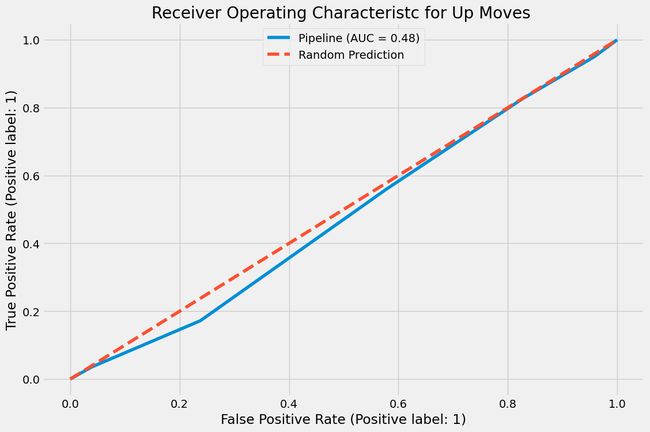
plot_roc_curve(pipe, X_test, y_test)
plt.plot(r_fpr, r_tpr, linestyle='dashed', label='Random Prediction')
plt.title("Receiver Operating Characteristc for Up Moves ")
plt.legend(loc=9)
plt.show()

我们再来看看分类报告。

# Classification Report
print(classification_report(y_test, y_pred))

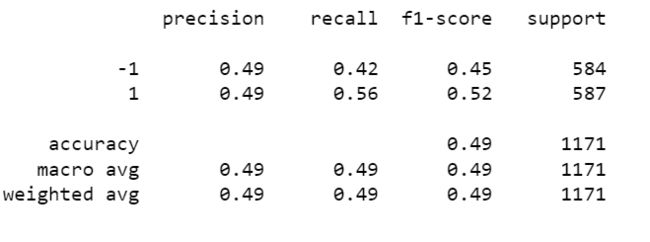
结果看起来并不是很好，是不是得对参数进行一些调整？实际应用中的情况一般是，我们想着调参，但实际大部分结果是，即便有调参，结果也一般般。没关系，我们先看一下。

超参数调优

超参数调优（Hyperparameter Tuning）是指在机器学习或深度学习模型中，通过系统地尝试不同的超参数组合，以找到最佳的超参数配置，以提高模型的性能和泛化能力。

超参数是指在训练模型之前需要设置的参数，其值不能通过训练过程自动学习得到，而是由数据科学家或机器学习工程师根据经验或试验设定的。常见的超参数包括学习率、正则化参数、批量大小、迭代次数等。

超参数调优的目标是找到最佳的超参数组合，使得模型在未见过的数据上表现出最佳的性能。通常，通过尝试不同的超参数组合，对模型进行训练和评估，然后根据评估结果调整超参数的值，不断迭代直到找到最佳的超参数配置。

常用的超参数调优方法包括：

1. 网格搜索（Grid Search）：在预先定义的超参数范围内，穷举所有可能的超参数组合，并根据交叉验证或验证集的性能评估来选择最佳组合。

2. 随机搜索（Random Search）：在预先定义的超参数范围内，随机选择一些超参数组合进行训练和评估，并根据性能评估结果来调整超参数的搜索范围，以逐步逼近最佳超参数组合。

3. 贝叶斯优化（Bayesian Optimization）：使用贝叶斯方法建立一个代理模型，根据已有的超参数组合和对应的性能评估结果，通过概率推断来选择下一个尝试的超参数组合，以逐步优化模型的性能。

4. 强化学习（Reinforcement Learning）：将超参数调优问题建模为一个强化学习问题，在模拟环境中通过试验和反馈来学习找到最佳超参数组合。

超参数调优是优化模型性能的重要步骤，能够改善模型的准确性、泛化能力和鲁棒性。通过选择最佳的超参数配置，可以提高模型的预测能力，并在实际应用中取得更好的效果。

本示例KNN方法的超参数是模型中使用的邻居个数k。

时间序列的交叉验证

时间序列交叉验证（Time Series Cross-Validation）是一种用于评估和选择时间序列模型的验证方法。与传统的交叉验证方法（如K折交叉验证）不同，时间序列交叉验证考虑了时间序列数据的时间顺序性，确保在模型评估过程中不会发生未来信息泄漏的情况。

在时间序列交叉验证中，数据集按照时间顺序划分为多个连续的训练集和测试集。具体的划分方式包括以下几种常见的方法：

1. 简单交叉验证（Simple Cross-Validation）：将数据集分为训练集和测试集两部分，通常按照时间顺序将最后一部分作为测试集，其余部分作为训练集。

2. 滚动窗口交叉验证（Rolling Window Cross-Validation）：从数据集的起始点开始，依次滑动一个固定大小的窗口，将窗口内的数据作为训练集，下一个时间步的数据作为测试集，重复进行模型评估。

3. 扩展窗口交叉验证（Expanding Window Cross-Validation）：从数据集的起始点开始，逐渐扩大窗口的大小，将窗口内的数据作为训练集，下一个时间步的数据作为测试集，重复进行模型评估。

时间序列交叉验证方法的关键在于确保测试集中的样本在训练集中的时间段之后，以避免模型使用未来信息进行训练和预测。这样可以更准确地模拟真实应用场景下的模型性能，并提供对模型的稳定性和泛化能力的评估。

在时间序列交叉验证过程中，可以使用各种评估指标（如均方误差、平均绝对误差、预测准确率等）来度量模型的性能，并根据评估结果选择最佳的模型配置、超参数或特征。

总之，时间序列交叉验证是一种针对时间序列数据的验证方法，能够更准确地评估时间序列模型的性能，提供对未来数据的预测能力的估计。

在时间序列分析中，前向链（Forward Chain）是一种用于生成和预测未来观测值的方法。它是基于当前已知观测值的值序列，通过递归地应用模型来预测未来观测值。为了保持顺序并使训练集先于测试集发生，我们使用前向链方法，其中模型最初以相同的窗口大小进行训练和测试。并且，对于每个后续折叠，训练窗口的大小增加，包括之前的训练数据和测试数据。新的测试窗口再次遵循训练窗口，但保持相同的长度。

让我们使用前向链来交叉验证5段时间序列数据，并获得新的训练和测试集。回想一下，目标是通过展望未来来创建的，因为我们必须提前一天查看股票回报，以预测股票是上涨还是下跌。对于前瞻性变量的数据泄露，我们必须设置gap=1。

# Cross-validdation
tscv = TimeSeriesSplit(n_splits=5, gap=1) 

Grid Search （网格搜索）

传统的超参数优化方式通常是使用网格搜索（也称为参数扫描）。它是对学习算法的超参数空间进行手动指定的穷举搜索。网格搜索算法必须依赖某种性能指标的指导，通常是通过在训练集上进行交叉验证或在验证集上进行评估来进行测量。

Grid Search（网格搜索）对于给定的估计器（estimator），对指定的参数值进行穷尽搜索。它实现了"fit"和"score"等方法。通过对参数网格进行交叉验证的网格搜索，优化了应用这些方法所使用的估计器的参数。

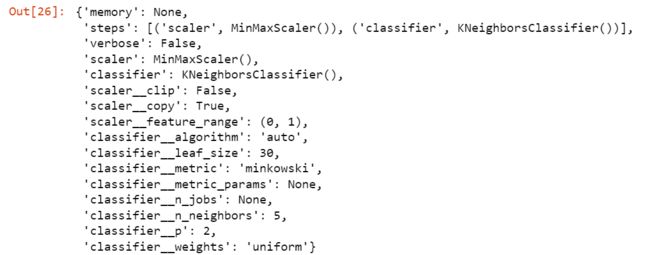
# Get parameters list
pipe.get_params()

# Perform GridSearch and fit
param_grid = {"classifier__n_neighbors" : np.arange(1, 51, 1)}    # k 选取1到51，间隔为1, 参数自给自定

grid_search = GridSearchCV(pipe, param_grid, scoring='roc_auc', n_jobs=-1, cv=tscv, verbose=1) 
# 原先默认regressior是R-sqr；现在指定AUC为优化目标，进行调参，找到一个最好的模型使得AUC面积最大
# 整好了，开始拟合
grid_search.fit(X_train, y_train)

# Best Params
grid_search.best_params_

# Best Score
grid_search.best_score_

也不是很好，因为分类的太平均了。得到了K=35，咱们再重新训练一次。

# Instantiate KNN model with search param 不用调参，不用规模化处理，不用pipe了
clf = KNeighborsClassifier(n_neighbors=grid_search.best_params_["classifier__n_neighbors"])

# Fit the model
clf.fit(X_train, y_train)

# Predicting the test dataset
y_pred = clf.predict(X_test)

# Measure Accuracy
acc_train = accuracy_score(y_train, clf.predict(X_train))
acc_test = accuracy_score(y_test, y_pred)

# Print Accuracy
print(f"\n Training Accuracy \t: {acc_train :0.4} \n Test Accuracy \t\t: {acc_test :0.4}" )

# Confusion Matrix for binary classification
tn, fp, fn, tp = confusion_matrix(y_test, y_pred).ravel()
print(tn,fp, fn, tp)

# Plot Confusion Matrix
plot_confusion_matrix(clf, X_test, y_test, cmap='Blues', values_format='.4g')
plt.title("Confusion Matrix")
plt.grid(False)

# Plot ROC curve 
# 画出来0.51，也没改变多少；一般来说得到一个0.6的，就是很好的了
plot_roc_curve(clf, X_test, y_test)

# Classification report
print(classification_report(y_test, y_pred))

通常情况下，AUC值达到0.6或更高时可以说模型较好。测试准确率和AUC值的数值显示，该模型的表现略优于随机猜测，但预测能力有限。AUC值为0.51表明该模型在区分两个类别方面并没有比随机猜测更好。AUC值为0.5表示模型与随机猜测相同，所以0.51的值只表示了微小的改进。

测试准确率为0.51，这意味着模型对超过一半的测试样本能正确预测二分类任务的结果。然而，这并不是非常高的准确率，表明仍有显著改进空间。

因为我们这里只是举例，大家可以用其他股票的数据或者构建投资组合来试试。

交易策略

根据我们定义的target（或分类器），我们制定交易策略。假设没有交易成本，如果出现买入信号，我们今天就会买入一股SPY股票；如果出现卖出信号，我们今天就会卖空一股SPY股票。

我们每次只操作一股股票的原因是为了使策略收益与未来收益之间的比较更加直观。

在提高准确性之后，应用KNN预测模型并生成一个名为"Signal"的新变量，表示对明天股票涨跌的预测，预测上涨，signal=1；预测下跌，signal=-1。

策略收益将计算为：
策略收益 = 未来收益 * Signal

# Subsume into a new dataframe
df1 = df.copy()                   # df[-len(X_test)]
df1['Signal'] = clf.predict(X)    # clf.predict(X_test)，预测出来的正负一，代表当天预测出来的明天的涨跌

# Strategy Returns
df1['Strategy'] = df1['Forward Returns'] * df1['Signal'].fillna(0)

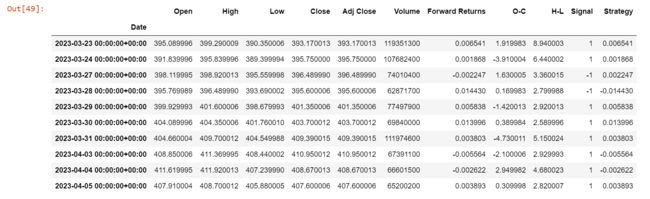
# Check the output
df1.tail(10)

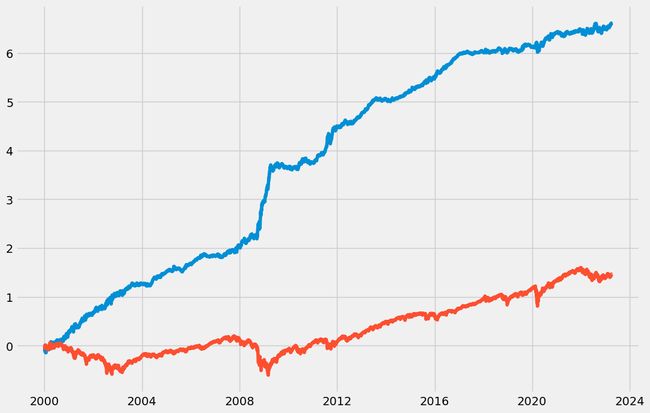
# plot
plt.plot(np.cumsum(df1['Strategy']))          #策略的累计回报
plt.plot(np.cumsum(df1['Forward Returns']))   #市场自身的累计回报

下图显示了市场收益(红线)和策略收益(蓝线)的累积总和。

回报分析

这里有一些代码可以绘制图表。

# !pip install pyfolio
import pyfolio as pf

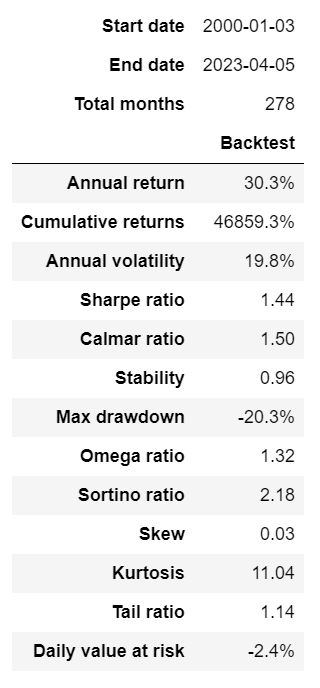
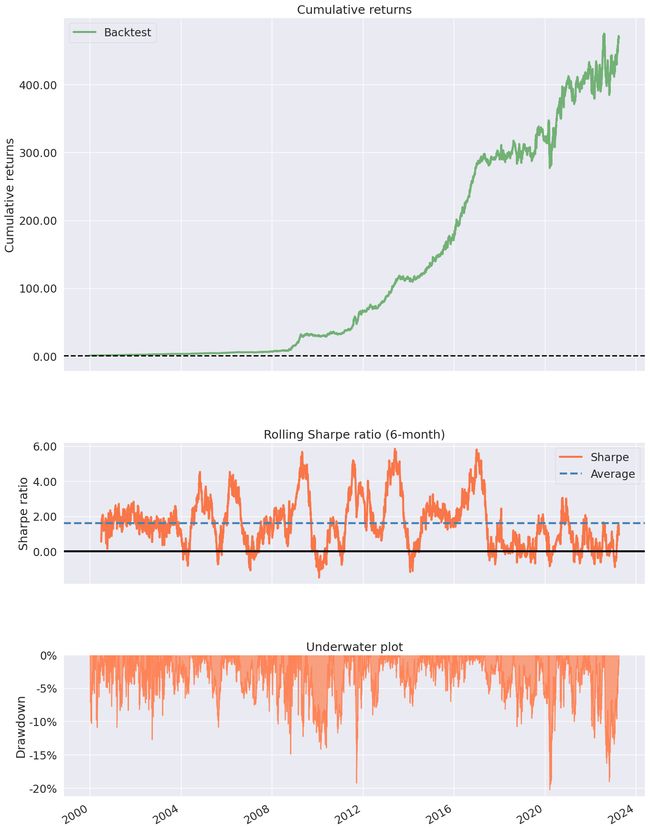
# Create Tear sheet using pyfolio for outsample - for X_test，这个策略回报率必须对应时间，不然参数对应不上
pf.create_simple_tear_sheet(df1['Strategy'])

也可以设置开始时间。示例如下：

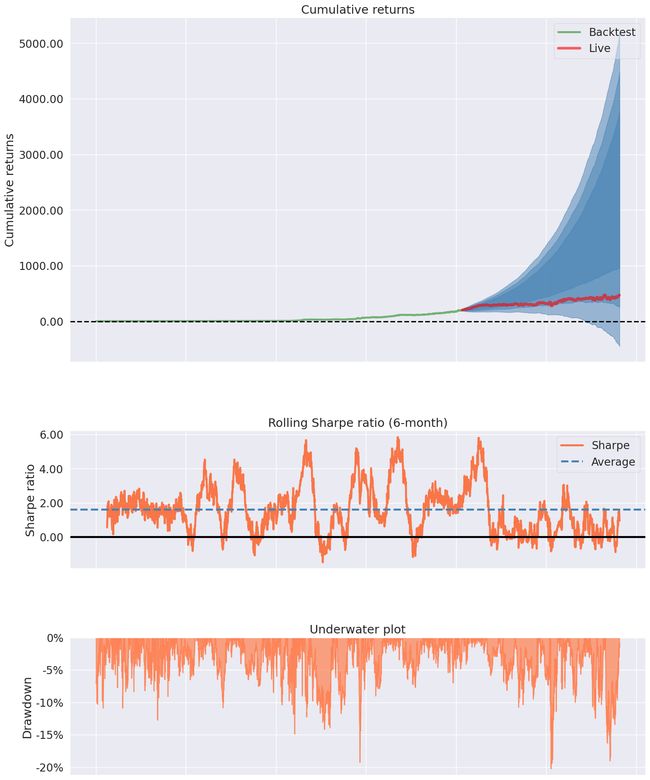
# Live start date 2016.4.7
pf.create_simple_tear_sheet(df1['Strategy'], live_start_date='2016-04-07')

绘制heatmap。

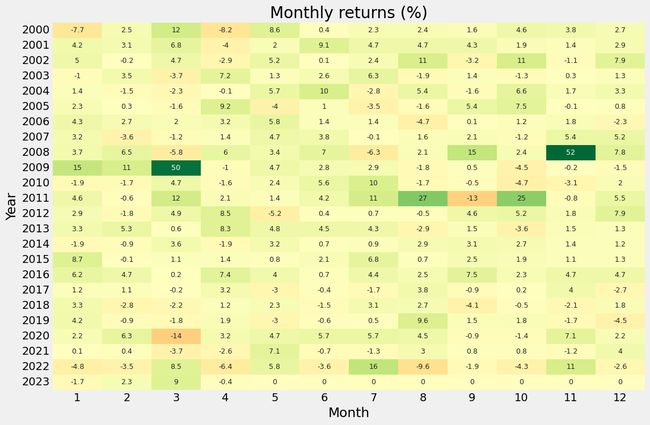
pf.plot_monthly_returns_heatmap(df1['Strategy'])

绘制年回报条形图。

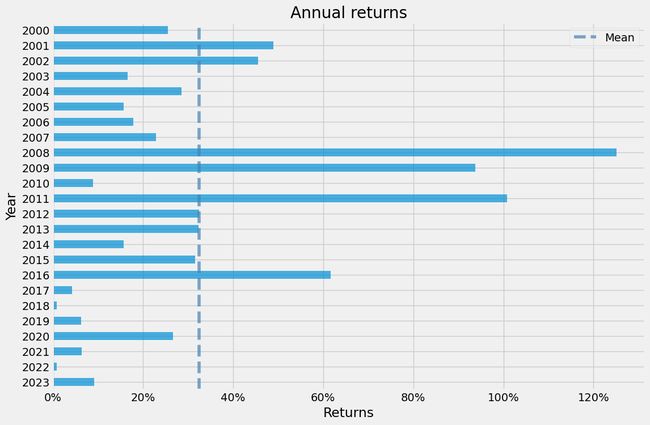
pf.plot_annual_returns(df1['Strategy'])

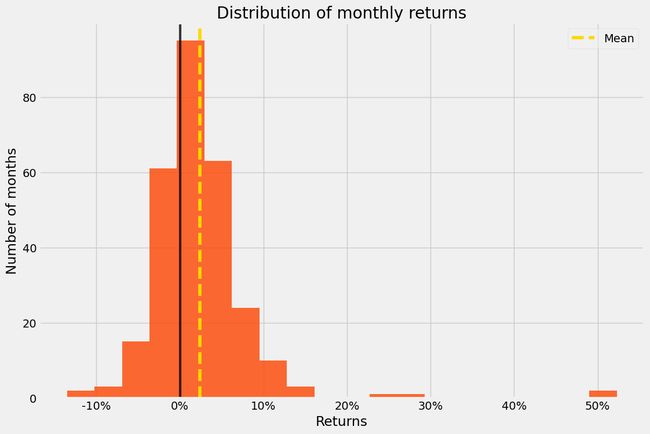
pf.plot_monthly_returns_dist(df1['Strategy'])