二叉树模型与期权定价

二叉树

二叉树法（Binomial Tree）是由Cox, Ross, 和 Robinstein在1979年首创的。

二叉树法是一种在金融学中用于估算期权价格的方法，其中二叉树模型用于模拟股票价格的变化。在二叉树模型中，每个节点表示股票的价格，在模拟期间，二叉树模型允许股票在下一个时间点向上或向下移动特定的数量。每个节点都有两个子节点，分别表示价格向上或向下变化后的价格。

给定初始股票价格 $S$，我们让它以 $u$ 和 $v$ 倍上升或下降，从而产生新的价格 $uS$ 和 $vS$。如果有两次向上移动，股票价格为 $u^{2}S$；如果有两次向下移动，股票价格则为 $v^{2}S$；如果有一次向上移动和一次向下移动，股票价格为 $uvS$；依此类推。我们可以将此扩展到任意数量的时间节点（time step）或分支（branch），这取决于你想怎么设置模型的复杂程度。一般我们会将时间总步长设置为直到期权到期为止。

为什么用系数u和v乘股票价格，而不用股票价格加或减某一特定值（eg. S+$\delta$S）?

在二叉树法中，节点的值不仅仅包括股票的价格，还需要考虑时间价值因素。因此，需要将每个节点的值设置为某个系数乘以股票的价格，这个系数通常是指数函数中的无风险利率和时间的折现因子。

将系数乘以股票价格而不是加法的原因是，系数表示的是无风险利率和时间的折现因子，是一个标准化的值。而股票价格是一个变化的值，不具有标准化的特性。通过将系数乘以股票价格，可以将股票价格和时间价值因素进行有效的分离，并在模拟期间准确地计算每个节点的值。

此外，如果使用加法而不是乘法，则可能会产生不正确的结果，因为这将忽略时间价值因素，从而导致期权价格的估算不准确。因此，在二叉树法中，使用系数乘以股票价格来计算每个节点的值，以确保模拟期权价格时考虑到时间价值因素。

导入库

画二叉树时，我用了别人做好的helper模块。引用索引会贴在最后面，大家感兴趣可以去看看。接下来导入示例所需要的库和helper模块。

# Import math functions from NumPy
from numpy import *

# Import plotting functions from helper 
import helper 

价格路径及路径的概率

到达二叉树中特定节点的概率取决于到达该节点的不同路径的数量以及向上和向下移动的概率。我们记向上移动的概率为p,在二叉树中，向下移动的概率为1-p。下图显示了到达每个节点的路径数量以及到达该节点的概率。下面我们使用helper模块来分别绘制价格路径及其概率

# Plot asset price path
plot_asset_path()

# Plot node probability
plot_probability()

风险中性概率

风险中性测度(risk-neutral measure)是一种概率测度。在风险中性测度下，今天的每个股价都是股价期望值的折现。二叉树模型中，基于风险中性假设，我们有：
标的金融工具会向上或向下移动至原来的$u$倍或$v$倍，范围为$u\ge 1$，$0\le v\le 1$。

$$u=1+\sigma \sqrt{\delta t}$$

$$v=1-\sigma \sqrt{\delta t}$$

风险中性概率$p^{\prime }$为
$$p^{\prime }=\frac{1}{2}+\frac{r\sqrt{\sigma t}}{2\sigma }$$

期权价格$V$是期望的现值：
$$V=\frac{1}{1+r\delta t}(p^{\prime }{V}^{+}+(1-p^{\prime })V^{-})$$

构建二叉树

构建二叉树的步骤分为：

1. 画一个 n-step tree；
2. 在第n步结束时，估计终端价格；
3. 根据终端价格、行权价格和类型，计算每个节点的期权价值；
4. 根据风险中性概率，将其折现回一步，即从n折现到n-1；
5. 重复前面的步骤，直到在步骤0中找到最终值。

二叉树定价模型

下面我们来建一个二叉树模型来进行期权定价。本示例中使用的是欧式看涨期权。

假设一欧式看涨期权的标的资产是某股票。给定当前股票价格$S_0$,期权的执行价格（strike price）为 $K$，期权到期日（expiration date）为 $T$，此时股票价值 $S_T$。

$$payoff=max(S_T-K,0)$$

# Create a user defined function
def binomial_option(spot, strike, rate, sigma, time, steps, output=0):
    
    """
    binomial_option(spot, strike, rate, sigma, time, steps, output=0)
    
    Function to calculate binomial option pricing for european call option
    
    Params
    ------
    spot       -int or float    - spot price
    strike     -int or float    - strike price
    rate       -float           - interest rate
    time       -int or float    - expiration time
    steps      -int             - number of time steps
    output     -int             - [0: price, 1: payoff, 2: option value, 3: option delta]
    
    Returns
    --------
    out: ndarray
    An array object of price, payoff, option value and delta as specified by the output flag
    
    """
    
    # define parameters
    ts = time / steps
    u  = 1 + sigma*sqrt(ts) 
    v  = 1 - sigma*sqrt(ts)
    p  = 0.5 + rate *sqrt(ts) / (2*sigma)
    df = 1/(1+rate*ts)
    
    # initialize the arrays
    px = zeros((steps+1, steps+1))
    cp = zeros((steps+1, steps+1))
    V = zeros((steps+1, steps+1))
    d = zeros((steps+1, steps+1))
    
    # binomial loop : forward loop
    for j in range(steps+1):
        for i in range(j+1):
            px[i,j] = spot * power(v,i) * power(u,j-i)
            cp[i,j] = maximum(px[i,j] - strike, 0)
         
    # reverse loop
    for j in range(steps+1, 0, -1):
        for i in range(j):
            if (j==steps+1):
                V[i,j-1] = cp[i,j-1]
                d[i,j-1] = 0 
            else:
                V[i,j-1] = df*(p*V[i,j]+(1-p)*V[i+1,j])
                d[i,j-1] = (V[i,j]-V[i+1,j])/(px[i,j]-px[i+1,j])
    
    results = around(px,2), around(cp,2), around(V,2), around(d,4)

    return results[output]

# Asset price
px = binomial_option(100,100,0.05,0.20,1,4,0)
px

# Intrinsic value of call options
cp = binomial_option(100,100,0.05,0.20,1,4,1)
cp

# Option price 
opt = binomial_option(100,100,0.05,0.20,1,4,2)
opt

# Option delta
delta = binomial_option(100,100,0.05,0.20,1,4,3)
delta

# Binomial Option Price
print(f"European Call Option Price using Binomial Tree Method: {opt[0,0]:.2f}")

European Call Option Price using Binomial Tree Method: 10.29
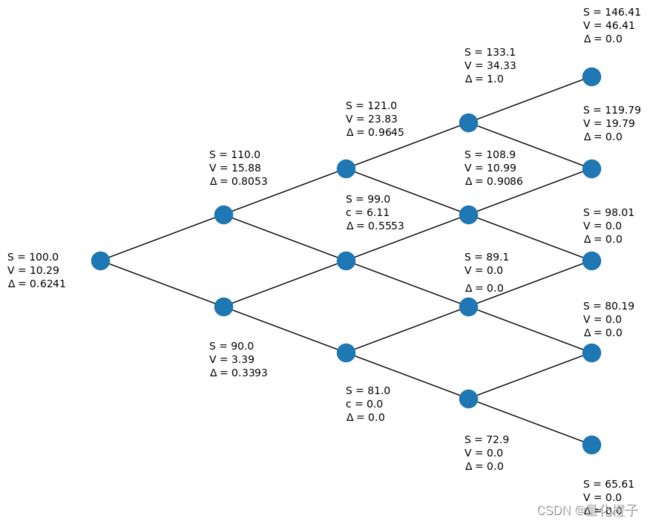
我们得到这个欧式期权价值 $10.29。

我们画出二叉树来展示一下计算过程。

# Plot a 4-Step Binomial Tree 
plot_binomial_tree(px[0,0], px, opt, delta)

Reference

helper.py

有小伙伴私信我说这个自定义模块找不到了，需要的话可以关注gzh：随机漫步的橙子，回复“代码”即可，以后博客用到的数据和其他资源都会放在gzh里。
yahoo finance的替代网页，不方便的需要下载数据可以戳：https://cn.investing.com/