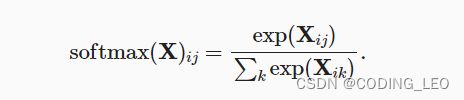softmax回归的从零开始实现

就像我们从零开始实现线性回归一样， 我们认为softmax回归也是重要的基础，因此应该知道实现softmax回归的细节。 本节我们将使用刚刚在引入的Fashion-MNIST数据集， 并设置数据迭代器的批量大小为256。

import torch
from IPython import display
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

1. 初始化模型参数

和之前线性回归的例子一样，这里的每个样本都将用固定长度的向量表示。 原始数据集中的每个样本都是28×28的图像。 本节将展平每个图像，把它们看作长度为784的向量。 在后面的章节中，我们将讨论能够利用图像空间结构的特征， 但现在我们暂时只把每个像素位置看作一个特征。

回想一下，在softmax回归中，我们的输出与类别一样多。 因为我们的数据集有10个类别，所以网络输出维度为10。 因此，权重将构成一个784×10的矩阵， 偏置将构成一个1×10的行向量。 与线性回归一样，我们将使用正态分布初始化我们的权重W，偏置初始化为0。

num_inputs = 784
num_outputs = 10

W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)

2. 定义softmax操作

在实现softmax回归模型之前，我们简要回顾一下sum运算符如何沿着张量中的特定维度工作。 如 2.3.6节和 2.3.6.1节所述， 给定一个矩阵X，我们可以对所有元素求和（默认情况下）。 也可以只求同一个轴上的元素，即同一列（轴0）或同一行（轴1）。 如果X是一个形状为(2, 3)的张量，我们对列进行求和， 则结果将是一个具有形状(3,)的向量。 当调用sum运算符时，我们可以指定保持在原始张量的轴数，而不折叠求和的维度。 这将产生一个具有形状(1, 3)的二维张量。

X = torch.tensor([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]])
X.sum(0, keepdim=True), X.sum(1, keepdim=True)

(tensor([[5., 7., 9.]]),
 tensor([[ 6.],
         [15.]]))

回想一下，实现softmax由三个步骤组成：

1. 对每个项求幂（使用exp）；

2. 对每一行求和（小批量中每个样本是一行），得到每个样本的规范化常数；

3. 将每一行除以其规范化常数，确保结果的和为1。

在查看代码之前，我们回顾一下这个表达式：

分母或规范化常数，有时也称为配分函数（其对数称为对数-配分函数）。 该名称来自统计物理学中一个模拟粒子群分布的方程。

def softmax(X):
    X_exp = torch.exp(X)
    partition = X_exp.sum(1, keepdim=True)
    return X_exp / partition  # 这里应用了广播机制

正如上述代码，对于任何随机输入，我们将每个元素变成一个非负数。 此外，依据概率原理，每行总和为1。

X = torch.normal(0, 1, (2, 5))
X_prob = softmax(X)
X_prob, X_prob.sum(1)

(tensor([[0.1686, 0.4055, 0.0849, 0.1064, 0.2347],
         [0.0217, 0.2652, 0.6354, 0.0457, 0.0321]]),
 tensor([1.0000, 1.0000]))

注意，虽然这在数学上看起来是正确的，但我们在代码实现中有点草率。 矩阵中的非常大或非常小的元素可能造成数值上溢或下溢，但我们没有采取措施来防止这点。