rgb2gray

SHAP（六）：使用 XGBoost 和 HyperOpt 进行信用卡欺诈检测

本笔记本介绍了 XGBoost Classifier 在金融行业中的实现，特别是在信用卡欺诈检测方面。构建 XGBoost 分类器后，它将使用 HyperOpt 库（sklearn 的 GridSearchCV 和 RandomziedSearchCV 算法的替代方案）来调整各种模型参数，目标是实现正常交易和欺诈交易分类的最大 f1 分数。作为模型评估的一部分，将计算 f1 分数度量，为分类构建混淆矩阵，生成分类报告并绘制精确召回曲线。最后，将根据 XGBoost 的内部算法以及特征重要性的 SHAP 实现来计算和绘制特征重要性。

来源：https://github.com/albazahm/Credit_Card_Fraud_Detection_with_XGBoost_and_HyperOpt/tree/master

1. Loading Libraries and Data

#loading libraries
import numpy as np
import pandas as pd 
import matplotlib.pyplot as plt
from sklearn.metrics import f1_score, make_scorer, confusion_matrix, classification_report, precision_recall_curve, plot_precision_recall_curve, average_precision_score, auc
from sklearn.model_selection import train_test_split
import seaborn as sns
from hyperopt import hp, fmin, tpe, Trials, STATUS_OK
import xgboost as xgb
import shap
# Any results you write to the current directory are saved as output.

/kaggle/input/creditcardfraud/creditcard.csv

#loading the data into a dataframe
credit_df = pd.read_csv('./creditcard.csv')

2. Data Overview

#preview of the first 10 rows of data
credit_df.head(10)

	Time	V1	V2	V3	V4	V5	V6	V7	V8	V9	...	V21	V22	V23	V24	V25	V26	V27	V28	Amount
0	0.0	-1.359807	-0.072781	2.536347	1.378155	-0.338321	0.462388	0.239599	0.098698	0.363787	...	-0.018307	0.277838	-0.110474	0.066928	0.128539	-0.189115	0.133558	-0.021053	149.62
1	0.0	1.191857	0.266151	0.166480	0.448154	0.060018	-0.082361	-0.078803	0.085102	-0.255425	...	-0.225775	-0.638672	0.101288	-0.339846	0.167170	0.125895	-0.008983	0.014724	2.69
2	1.0	-1.358354	-1.340163	1.773209	0.379780	-0.503198	1.800499	0.791461	0.247676	-1.514654	...	0.247998	0.771679	0.909412	-0.689281	-0.327642	-0.139097	-0.055353	-0.059752	378.66
3	1.0	-0.966272	-0.185226	1.792993	-0.863291	-0.010309	1.247203	0.237609	0.377436	-1.387024	...	-0.108300	0.005274	-0.190321	-1.175575	0.647376	-0.221929	0.062723	0.061458	123.50
4	2.0	-1.158233	0.877737	1.548718	0.403034	-0.407193	0.095921	0.592941	-0.270533	0.817739	...	-0.009431	0.798278	-0.137458	0.141267	-0.206010	0.502292	0.219422	0.215153	69.99
5	2.0	-0.425966	0.960523	1.141109	-0.168252	0.420987	-0.029728	0.476201	0.260314	-0.568671	...	-0.208254	-0.559825	-0.026398	-0.371427	-0.232794	0.105915	0.253844	0.081080	3.67
6	4.0	1.229658	0.141004	0.045371	1.202613	0.191881	0.272708	-0.005159	0.081213	0.464960	...	-0.167716	-0.270710	-0.154104	-0.780055	0.750137	-0.257237	0.034507	0.005168	4.99
7	7.0	-0.644269	1.417964	1.074380	-0.492199	0.948934	0.428118	1.120631	-3.807864	0.615375	...	1.943465	-1.015455	0.057504	-0.649709	-0.415267	-0.051634	-1.206921	-1.085339	40.80
8	7.0	-0.894286	0.286157	-0.113192	-0.271526	2.669599	3.721818	0.370145	0.851084	-0.392048	...	-0.073425	-0.268092	-0.204233	1.011592	0.373205	-0.384157	0.011747	0.142404	93.20
9	9.0	-0.338262	1.119593	1.044367	-0.222187	0.499361	-0.246761	0.651583	0.069539	-0.736727	...	-0.246914	-0.633753	-0.120794	-0.385050	-0.069733	0.094199	0.246219	0.083076	3.68

10 rows × 31 columns

#displaying descriptive statistics
credit_df.describe()

	Time	V1	V2	V3	V4	V5	V6	V7	V8	V9	...	V21	V22	V23	V24	V25	V26	V27	V28	Amount	Class
count	284807.000000	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	...	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	284807.000000	284807.000000
mean	94813.859575	3.919560e-15	5.688174e-16	-8.769071e-15	2.782312e-15	-1.552563e-15	2.010663e-15	-1.694249e-15	-1.927028e-16	-3.137024e-15	...	1.537294e-16	7.959909e-16	5.367590e-16	4.458112e-15	1.453003e-15	1.699104e-15	-3.660161e-16	-1.206049e-16	88.349619	0.001727
std	47488.145955	1.958696e+00	1.651309e+00	1.516255e+00	1.415869e+00	1.380247e+00	1.332271e+00	1.237094e+00	1.194353e+00	1.098632e+00	...	7.345240e-01	7.257016e-01	6.244603e-01	6.056471e-01	5.212781e-01	4.822270e-01	4.036325e-01	3.300833e-01	250.120109	0.041527
min	0.000000	-5.640751e+01	-7.271573e+01	-4.832559e+01	-5.683171e+00	-1.137433e+02	-2.616051e+01	-4.355724e+01	-7.321672e+01	-1.343407e+01	...	-3.483038e+01	-1.093314e+01	-4.480774e+01	-2.836627e+00	-1.029540e+01	-2.604551e+00	-2.256568e+01	-1.543008e+01	0.000000	0.000000
25%	54201.500000	-9.203734e-01	-5.985499e-01	-8.903648e-01	-8.486401e-01	-6.915971e-01	-7.682956e-01	-5.540759e-01	-2.086297e-01	-6.430976e-01	...	-2.283949e-01	-5.423504e-01	-1.618463e-01	-3.545861e-01	-3.171451e-01	-3.269839e-01	-7.083953e-02	-5.295979e-02	5.600000	0.000000
50%	84692.000000	1.810880e-02	6.548556e-02	1.798463e-01	-1.984653e-02	-5.433583e-02	-2.741871e-01	4.010308e-02	2.235804e-02	-5.142873e-02	...	-2.945017e-02	6.781943e-03	-1.119293e-02	4.097606e-02	1.659350e-02	-5.213911e-02	1.342146e-03	1.124383e-02	22.000000	0.000000
75%	139320.500000	1.315642e+00	8.037239e-01	1.027196e+00	7.433413e-01	6.119264e-01	3.985649e-01	5.704361e-01	3.273459e-01	5.971390e-01	...	1.863772e-01	5.285536e-01	1.476421e-01	4.395266e-01	3.507156e-01	2.409522e-01	9.104512e-02	7.827995e-02	77.165000	0.000000
max	172792.000000	2.454930e+00	2.205773e+01	9.382558e+00	1.687534e+01	3.480167e+01	7.330163e+01	1.205895e+02	2.000721e+01	1.559499e+01	...	2.720284e+01	1.050309e+01	2.252841e+01	4.584549e+00	7.519589e+00	3.517346e+00	3.161220e+01	3.384781e+01	25691.160000	1.000000

8 rows × 31 columns

#exploring datatypes and count of non-NULL rows for each feature
credit_df.info()


RangeIndex: 284807 entries, 0 to 284806
Data columns (total 31 columns):
Time      284807 non-null float64
V1        284807 non-null float64
V2        284807 non-null float64
V3        284807 non-null float64
V4        284807 non-null float64
V5        284807 non-null float64
V6        284807 non-null float64
V7        284807 non-null float64
V8        284807 non-null float64
V9        284807 non-null float64
V10       284807 non-null float64
V11       284807 non-null float64
V12       284807 non-null float64
V13       284807 non-null float64
V14       284807 non-null float64
V15       284807 non-null float64
V16       284807 non-null float64
V17       284807 non-null float64
V18       284807 non-null float64
V19       284807 non-null float64
V20       284807 non-null float64
V21       284807 non-null float64
V22       284807 non-null float64
V23       284807 non-null float64
V24       284807 non-null float64
V25       284807 non-null float64
V26       284807 non-null float64
V27       284807 non-null float64
V28       284807 non-null float64
Amount    284807 non-null float64
Class     284807 non-null int64
dtypes: float64(30), int64(1)
memory usage: 67.4 MB

3. Data Preparation

在这里，我们查找并删除数据中的重复观测值，定义用于分类的自变量 (X) 和因变量 (Y)，并分离出验证集和测试集。

#checking for duplicated observations
credit_df.duplicated().value_counts()

False    283726
True       1081
dtype: int64

#dropping duplicated observations
credit_df = credit_df.drop_duplicates()

#defining independent (X) and dependent (Y) variables from dataframe
X = credit_df.drop(columns = 'Class')
Y = credit_df['Class'].values

#splitting a testing set from the data
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size = 0.20, stratify = Y, random_state = 42)
#splitting a validation set from the training set to tune parameters
X_train, X_val, Y_train, Y_val = train_test_split(X_train, Y_train, test_size = 0.20, stratify = Y_train, random_state = 42)

4. Model Set-Up and Training

在本节中，我们基于 f1 度量创建一个评分器，并为 XGBoost 模型定义参数搜索空间。此外，我们定义了一个包含分类器的函数，提取其预测，计算损失并将其提供给优化器。最后，我们使用所需的设置初始化优化器，运行它并查看试验中的参数和分数。

#creating a scorer from the f1-score metric
f1_scorer = make_scorer(f1_score)

# defining the space for hyperparameter tuning
space = {'eta': hp.uniform("eta", 0.1, 1),
        'max_depth': hp.quniform("max_depth", 3, 18, 1),
        'gamma': hp.uniform ('gamma', 1,9),
        'reg_alpha' : hp.quniform('reg_alpha', 50, 200, 1),
        'reg_lambda' : hp.uniform('reg_lambda', 0, 1),
        'colsample_bytree' : hp.uniform('colsample_bytree', 0.5, 1),
        'min_child_weight' : hp.quniform('min_child_weight', 0, 10, 1),
        'n_estimators': hp.quniform('n_estimators', 100, 200, 10)
        }

#defining function to optimize
def hyperparameter_tuning(space):
    clf = xgb.XGBClassifier(n_estimators = int(space['n_estimators']),       #number of trees to use
                            eta = space['eta'],                              #learning rate
                            max_depth = int(space['max_depth']),             #depth of trees
                            gamma = space['gamma'],                          #loss reduction required to further partition tree
                            reg_alpha = int(space['reg_alpha']),             #L1 regularization for weights
                            reg_lambda = space['reg_lambda'],                #L2 regularization for weights
                            min_child_weight = space['min_child_weight'],    #minimum sum of instance weight needed in child
                            colsample_bytree = space['colsample_bytree'],    #ratio of column sampling for each tree
                            nthread = -1)                                    #number of parallel threads used
    
    evaluation = [(X_train, Y_train), (X_val, Y_val)]
    
    clf.fit(X_train, Y_train,
            eval_set = evaluation,
            early_stopping_rounds = 10,
            verbose = False)

    pred = clf.predict(X_val)
    pred = [1 if i>= 0.5 else 0 for i in pred]
    f1 = f1_score(Y_val, pred)
    print ("SCORE:", f1)
    return {'loss': -f1, 'status': STATUS_OK }

# run the hyper paramter tuning
trials = Trials()
best = fmin(fn = hyperparameter_tuning,
            space = space,
            algo = tpe.suggest,
            max_evals = 100,
            trials = trials)

print (best)

SCORE:                                                 
0.7552447552447553                                     
SCORE:                                                                            
0.0                                                                               
SCORE:                                                                            
0.0                                                                               
SCORE:                                                                            
0.0                                                                               
SCORE:                                                                            
0.0                                                                               
SCORE:                                                                            
0.0                                                                               
SCORE:                                                                            
0.0                                                                               
SCORE:                                                                            
0.0                                                                               
SCORE:                                                                            
0.0                                                                               
SCORE:                                                                            
0.0                                                                               
SCORE:                                                                             
0.8169014084507042                                                                 
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.6666666666666666                                                                 
SCORE:                                                                             
0.7737226277372262                                                                 
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.8169014084507042                                                                 
SCORE:                                                                             
0.8169014084507042                                                                 
SCORE:                                                                             
0.8169014084507042                                                                 
SCORE:                                                                             
0.7891156462585034                                                                 
SCORE:                                                                             
0.7401574803149605                                                                 
SCORE:                                                                             
0.7737226277372262                                                                 
SCORE:                                                                             
0.7971014492753624                                                                 
SCORE:                                                                             
0.7499999999999999                                                                 
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.7552447552447553                                                                 
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.7883211678832117                                                                 
SCORE:                                                                             
0.7891156462585034                                                                 
SCORE:                                                                             
0.7737226277372262                                                                 
SCORE:                                                                             
0.782608695652174                                                                  
SCORE:                                                                             
0.8055555555555555                                                                 
SCORE:                                                                             
0.7401574803149605                                                                 
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.7552447552447553                                                                 
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.7737226277372262                                                                 
SCORE:                                                                             
0.7499999999999999                                                                 
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.8085106382978723                                                                 
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.7401574803149605                                                                 
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.7972972972972973                                                                 
SCORE:                                                                             
0.608695652173913                                                                  
SCORE:                                                                             
0.7552447552447553                                                                 
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.7384615384615385                                                                 
SCORE:                                                                             
0.8169014084507042                                                                 
SCORE:                                                                             
0.802919708029197                                                                  
SCORE:                                                                             
0.8169014084507042                                                                 
SCORE:                                                                             
0.8201438848920864                                                                 
SCORE:                                                                             
0.8201438848920864                                                                 
SCORE:                                                                             
0.8201438848920864                                                                 
SCORE:                                                                             
0.8085106382978723                                                                 
SCORE:                                                                             
0.8169014084507042                                                                 
SCORE:                                                                             
0.8085106382978723                                                                 
SCORE:                                                                             
0.7910447761194029                                                                 
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.7819548872180451                                                                 
SCORE:                                                                             
0.802919708029197                                                                  
SCORE:                                                                             
0.8085106382978723                                                                 
SCORE:                                                                             
0.8169014084507042                                                                 
SCORE:                                                                             
0.7910447761194029                                                                 
SCORE:                                                                             
0.7910447761194029                                                                 
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.7999999999999999                                                                 
SCORE:                                                                             
0.8085106382978723                                                                 
SCORE:                                                                             
0.8169014084507042                                                                 
SCORE:                                                                             
0.7692307692307692                                                                 
SCORE:                                                                             
0.7999999999999999                                                                 
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.7737226277372262                                                                 
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.7301587301587301                                                                 
SCORE:                                                                             
0.7786259541984732                                                                 
SCORE:                                                                             
0.7878787878787878                                                                 
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.7878787878787878                                                                 
SCORE:                                                                             
0.7692307692307692                                                                 
SCORE:                                                                             
0.0                                                                                
SCORE:                                                                             
0.7499999999999999                                                                 
SCORE:                                                                             
0.8169014084507042                                                                 
SCORE:                                                                             
0.7910447761194029                                                                 
100%|██████████| 100/100 [11:24<00:00,  6.84s/trial, best loss: -0.8201438848920864]
{'colsample_bytree': 0.9999995803500363, 'eta': 0.1316102455832729, 'gamma': 1.6313395777817137, 'max_depth': 5.0, 'min_child_weight': 3.0, 'n_estimators': 100.0, 'reg_alpha': 47.0, 'reg_lambda': 0.4901343161108276}

#plotting feature space and f1-scores for the different trials
parameters = space.keys()
cols = len(parameters)

f, axes = plt.subplots(nrows=1, ncols=cols, figsize=(20,5))
cmap = plt.cm.jet
for i, val in enumerate(parameters):
    xs = np.array([t['misc']['vals'][val] for t in trials.trials]).ravel()
    ys = [-t['result']['loss'] for t in trials.trials]
    xs, ys = zip(*sorted(zip(xs, ys)))
    axes[i].scatter(xs, ys, s=20, linewidth=0.01, alpha=0.25, c=cmap(float(i)/len(parameters)))
    axes[i].set_title(val)
    axes[i].grid()

#printing best model parameters
print(best)

{'colsample_bytree': 0.9999995803500363, 'eta': 0.1316102455832729, 'gamma': 1.6313395777817137, 'max_depth': 5.0, 'min_child_weight': 3.0, 'n_estimators': 100.0, 'reg_alpha': 47.0, 'reg_lambda': 0.4901343161108276}

5. Model Test and Evaluation

本节将探讨并可视化模型在测试数据上的表现。

#initializing XGBoost Classifier with best model parameters
best_clf = xgb.XGBClassifier(n_estimators = int(best['n_estimators']), 
                            eta = best['eta'], 
                            max_depth = int(best['max_depth']), 
                            gamma = best['gamma'], 
                            reg_alpha = int(best['reg_alpha']), 
                            min_child_weight = best['min_child_weight'], 
                            colsample_bytree = best['colsample_bytree'], 
                            nthread = -1)

#fitting XGBoost Classifier with best model parameters to training data
best_clf.fit(X_train, Y_train)

XGBClassifier(base_score=0.5, booster='gbtree', colsample_bylevel=1,
              colsample_bynode=1, colsample_bytree=0.9999995803500363,
              eta=0.1316102455832729, gamma=1.6313395777817137,
              learning_rate=0.1, max_delta_step=0, max_depth=5,
              min_child_weight=3.0, missing=None, n_estimators=100, n_jobs=1,
              nthread=-1, objective='binary:logistic', random_state=0,
              reg_alpha=47, reg_lambda=1, scale_pos_weight=1, seed=None,
              silent=None, subsample=1, verbosity=1)

#using the model to predict on the test set
Y_pred = best_clf.predict(X_test)

#printing f1 score of test set predictions
print('The f1-score on the test data is: {0:.2f}'.format(f1_score(Y_test, Y_pred)))

The f1-score on the test data is: 0.74

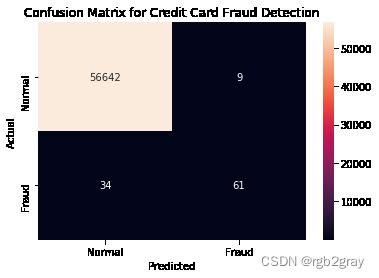
#creating a confusion matrix and labels
cm = confusion_matrix(Y_test, Y_pred)
labels = ['Normal', 'Fraud']

#plotting the confusion matrix
sns.heatmap(cm, annot = True, xticklabels = labels, yticklabels = labels, fmt = 'd')
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.title('Confusion Matrix for Credit Card Fraud Detection')

Text(0.5, 1.0, 'Confusion Matrix for Credit Card Fraud Detection')

#printing classification report
print(classification_report(Y_test, Y_pred))

              precision    recall  f1-score   support

           0       1.00      1.00      1.00     56651
           1       0.87      0.64      0.74        95

    accuracy                           1.00     56746
   macro avg       0.94      0.82      0.87     56746
weighted avg       1.00      1.00      1.00     56746

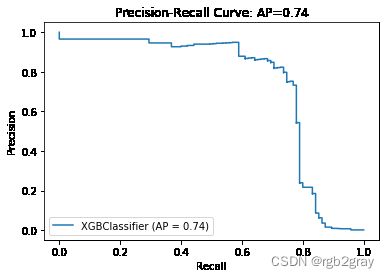
Y_score = best_clf.predict_proba(X_test)[:, 1]
average_precision = average_precision_score(Y_test, Y_score)
fig = plot_precision_recall_curve(best_clf, X_test, Y_test)
fig.ax_.set_title('Precision-Recall Curve: AP={0:.2f}'.format(average_precision))

Text(0.5, 1.0, 'Precision-Recall Curve: AP=0.74')

6. Feature Importances

本节将介绍两种算法，一种在 XGBoost 中，一种在 SHAP 中，用于可视化特征重要性。不幸的是，由于该数据集的特征是使用主成分分析（PCA）进行编码的，因此我们无法凭直觉得出模型如何从实际角度预测正常交易和欺诈交易的结论。

#extracting the booster from model
booster = best_clf.get_booster()

# scoring features based on information gain
importance = booster.get_score(importance_type = "gain")

#rounding importances to 2 decimal places
for key in importance.keys():
    importance[key] = round(importance[key],2)

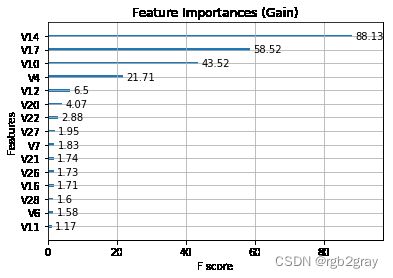
# plotting feature importances
ax = xgb.plot_importance(importance, importance_type='gain', show_values=True)
plt.title('Feature Importances (Gain)')
plt.show()

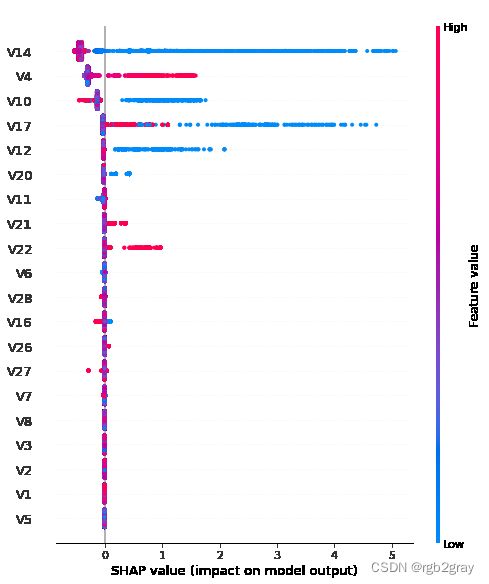
#obtaining SHAP values for XGBoost Model
explainer = shap.TreeExplainer(best_clf)
shap_values = explainer.shap_values(X_train)

#plotting SHAP Values of Feature Importances
shap.summary_plot(shap_values, X_train)

机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
理解Gunicorn：Python WSGI服务器的基石范范0825 ipython linux 运维
理解Gunicorn：PythonWSGI服务器的基石介绍Gunicorn，全称GreenUnicorn，是一个为PythonWSGI（WebServerGatewayInterface）应用设计的高效、轻量级HTTP服务器。作为PythonWeb应用部署的常用工具，Gunicorn以其高性能和易用性著称。本文将介绍Gunicorn的基本概念、安装和配置，帮助初学者快速上手。1.什么是Gunico
Python数据分析与可视化实战指南 William数据分析 python python 数据
在数据驱动的时代，Python因其简洁的语法、强大的库生态系统以及活跃的社区，成为了数据分析与可视化的首选语言。本文将通过一个详细的案例，带领大家学习如何使用Python进行数据分析，并通过可视化来直观呈现分析结果。一、环境准备1.1安装必要库在开始数据分析和可视化之前，我们需要安装一些常用的库。主要包括pandas、numpy、matplotlib和seaborn等。这些库分别用于数据处理、数学
python os.environ 江湖偌大 python 深度学习
os.environ['TF_CPP_MIN_LOG_LEVEL']='0'#默认值，输出所有信息os.environ['TF_CPP_MIN_LOG_LEVEL']='1'#屏蔽通知信息（INFO）os.environ['TF_CPP_MIN_LOG_LEVEL']='2'#屏蔽通知信息和警告信息（INFO\WARNING）os.environ['TF_CPP_MIN_LOG_LEVEL']='
Python中os.environ基本介绍及使用方法鹤冲天Pro #Python python 服务器开发语言
文章目录python中os.environos.environ简介os.environ进行环境变量的增删改查python中os.environ的使用详解1.简介2.key字段详解2.1常见key字段3.os.environ.get()用法4.环境变量的增删改查和判断是否存在4.1新增环境变量4.2更新环境变量4.3获取环境变量4.4删除环境变量4.5判断环境变量是否存在python中os.envi
Pyecharts数据可视化大屏：打造沉浸式数据分析体验我的运维人生信息可视化数据分析数据挖掘运维开发技术共享
Pyecharts数据可视化大屏：打造沉浸式数据分析体验在当今这个数据驱动的时代，如何将海量数据以直观、生动的方式展现出来，成为了数据分析师和企业决策者关注的焦点。Pyecharts，作为一款基于Python的开源数据可视化库，凭借其丰富的图表类型、灵活的配置选项以及高度的定制化能力，成为了构建数据可视化大屏的理想选择。本文将深入探讨如何利用Pyecharts打造数据可视化大屏，并通过实际代码案例
Python教程：一文了解使用Python处理XPath 旦莫 Python进阶 python 开发语言
目录1.环境准备1.1安装lxml1.2验证安装2.XPath基础2.1什么是XPath？2.2XPath语法2.3示例XML文档3.使用lxml解析XML3.1解析XML文档3.2查看解析结果4.XPath查询4.1基本路径查询4.2使用属性查询4.3查询多个节点5.XPath的高级用法5.1使用逻辑运算符5.2使用函数6.实战案例6.1从网页抓取数据6.1.1安装Requests库6.1.2代
python os.environ_python os.environ 读取和设置环境变量 weixin_39605414 python os.environ
>>>importos>>>os.environ.keys()['LC_NUMERIC','GOPATH','GOROOT','GOBIN','LESSOPEN','SSH_CLIENT','LOGNAME','USER','HOME','LC_PAPER','PATH','DISPLAY','LANG','TERM','SHELL','J2REDIR','LC_MONETARY','QT_QPA
高端密码学院笔记285 柚子_b4b4
高端幸福密码学院（高级班）幸福使者：李华第（598）期《幸福》之回归内在深层生命原动力基础篇——揭秘“激励”成长的喜悦心理案例分析主讲：刘莉一，知识扩充:成功=艰苦劳动+正确方法+少说空话。贪图省力的船夫，目标永远下游。智者的梦再美，也不如愚人实干的脚印。幸福早课堂2020.10.16星期五一笔记:1，重视和珍惜的前提是知道它的价值非常重要，当你珍惜了，你就真正定下来，真正的学到身上。2，大家需要
探索OpenAI和LangChain的适配器集成：轻松切换模型提供商 nseejrukjhad langchain easyui 前端 python
#探索OpenAI和LangChain的适配器集成：轻松切换模型提供商##引言在人工智能和自然语言处理的世界中，OpenAI的模型提供了强大的能力。然而，随着技术的发展，许多人开始探索其他模型以满足特定需求。LangChain作为一个强大的工具，集成了多种模型提供商，通过提供适配器，简化了不同模型之间的转换。本篇文章将介绍如何使用LangChain的适配器与OpenAI集成，以便轻松切换模型提供商
使用Faiss进行高效相似度搜索 llzwxh888 faiss python
在现代AI应用中，快速和高效的相似度搜索是至关重要的。Faiss（FacebookAISimilaritySearch）是一个专门用于快速相似度搜索和聚类的库，特别适用于高维向量。本文将介绍如何使用Faiss来进行相似度搜索，并结合Python代码演示其基本用法。什么是Faiss？Faiss是一个由FacebookAIResearch团队开发的开源库，主要用于高维向量的相似性搜索和聚类。Faiss
python是什么意思中文-在python中%是什么意思编程大乐趣
Python中%有两种：1、数值运算：%代表取模，返回除法的余数。如：>>>7%212、%操作符（字符串格式化，stringformatting），说明如下：%[(name)][flags][width].[precision]typecode(name)为命名flags可以有+，-，''或0。+表示右对齐。-表示左对齐。''为一个空格，表示在正数的左侧填充一个空格，从而与负数对齐。0表示使用0填
深入理解 MultiQueryRetriever：提升向量数据库检索效果的强大工具 nseejrukjhad 数据库 python
深入理解MultiQueryRetriever：提升向量数据库检索效果的强大工具引言在人工智能和自然语言处理领域，高效准确的信息检索一直是一个关键挑战。传统的基于距离的向量数据库检索方法虽然广泛应用，但仍存在一些局限性。本文将介绍一种创新的解决方案：MultiQueryRetriever，它通过自动生成多个查询视角来增强检索效果，提高结果的相关性和多样性。MultiQueryRetriever的工
Day1笔记-Python简介&标识符和关键字&输入输出 ~在杰难逃~ Python python 开发语言大数据数据分析数据挖掘
大家好，从今天开始呢，杰哥开展一个新的专栏，当然，数据分析部分也会不定时更新的，这个新的专栏主要是讲解一些Python的基础语法和知识，帮助0基础的小伙伴入门和学习Python，感兴趣的小伙伴可以开始认真学习啦！一、Python简介【了解】1.计算机工作原理编程语言就是用来定义计算机程序的形式语言。我们通过编程语言来编写程序代码，再通过语言处理程序执行向计算机发送指令，让计算机完成对应的工作，编程
python八股文面试题分享及解析(1) Shawn________ python
#1.'''a=1b=2不用中间变量交换a和b'''#1.a=1b=2a,b=b,aprint(a)print(b)结果：21#2.ll=[]foriinrange(3):ll.append({'num':i})print(11)结果:#[{'num':0},{'num':1},{'num':2}]#3.kk=[]a={'num':0}foriinrange(3):#0,12#可变类型，不仅仅改变
人工智能时代，程序员如何保持核心竞争力？ jmoych 人工智能
随着AIGC（如chatgpt、midjourney、claude等）大语言模型接二连三的涌现，AI辅助编程工具日益普及，程序员的工作方式正在发生深刻变革。有人担心AI可能取代部分编程工作，也有人认为AI是提高效率的得力助手。面对这一趋势,程序员应该如何应对?是专注于某个领域深耕细作，还是广泛学习以适应快速变化的技术环境?又或者，我们是否应该将重点转向AI无法轻易替代的软技能？让我们一起探讨程序员
每日算法&面试题，大厂特训二十八天——第二十天（树）肥学 ⚡算法题⚡面试题每日精进 java 算法数据结构
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题，最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧！！特别介绍小白练手专栏，适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
Python快速入门 —— 第三节：类与对象孤华暗香 Python快速入门 python 开发语言
第三节：类与对象目标：了解面向对象编程的基础概念，并学会如何定义类和创建对象。内容：类与对象：定义类：class关键字。类的构造函数：__init__()。类的属性和方法。对象的创建与使用。示例：classStudent:def__init__(self,name,age,major):self.name&#
pyecharts——绘制柱形图折线图 2224070247 信息可视化 python java 数据可视化
一、pyecharts概述自2013年6月百度EFE(ExcellentFrontEnd）数据可视化团队研发的ECharts1.0发布到GitHub网站以来，ECharts一直备受业界权威的关注并获得广泛好评，成为目前成熟且流行的数据可视化图表工具，被应用到诸多数据可视化的开发领域。Python作为数据分析领域最受欢迎的语言，也加入ECharts的使用行列，并研发出方便Python开发者使用的数据
Python 实现图片裁剪（附代码） | Python工具剑客阿良_ALiang
前言本文提供将图片按照自定义尺寸进行裁剪的工具方法，一如既往的实用主义。环境依赖ffmpeg环境安装，可以参考我的另一篇文章：windowsffmpeg安装部署_阿良的博客-CSDN博客本文主要使用到的不是ffmpeg，而是ffprobe也在上面这篇文章中的zip包中。ffmpy安装：pipinstallffmpy-ihttps://pypi.douban.com/simple代码不废话了，上代码
【华为OD技术面试真题 - 技术面】- python八股文真题题库（4) 算法大师华为od 面试 python
华为OD面试真题精选专栏：华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选**1.Python中的`with`**用途和功能自动资源管理示例：文件操作上下文管理协议示例代码工作流程解析优点2.\_\_new\_\_和**\_\_init\_\_**区别__new____init__区别总结3.**切片（Slicing）操作**基本切片语法
python os 环境变量 CV矿工 python 开发语言 numpy
环境变量：环境变量是程序和操作系统之间的通信方式。有些字符不宜明文写进代码里，比如数据库密码，个人账户密码，如果写进自己本机的环境变量里，程序用的时候通过os.environ.get（）取出来就行了。os.environ是一个环境变量的字典。环境变量的相关操作importos"""设置/修改环境变量：os.environ[‘环境变量名称’]=‘环境变量值’#其中key和value均为string类
Python爬虫解析工具之xpath使用详解 eqa11 python 爬虫开发语言
文章目录Python爬虫解析工具之xpath使用详解一、引言二、环境准备1、插件安装2、依赖库安装三、xpath语法详解1、路径表达式2、通配符3、谓语4、常用函数四、xpath在Python代码中的使用1、文档树的创建2、使用xpath表达式3、获取元素内容和属性五、总结Python爬虫解析工具之xpath使用详解一、引言在Python爬虫开发中，数据提取是一个至关重要的环节。xpath作为一门
【华为OD技术面试真题 - 技术面】- python八股文真题题库（1）算法大师华为od 面试 python
华为OD面试真题精选专栏：华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选1.数据预处理流程数据预处理的主要步骤工具和库2.介绍线性回归、逻辑回归模型线性回归（LinearRegression）模型形式：关键点：逻辑回归（LogisticRegression）模型形式：关键点：参数估计与评估：3.python浅拷贝及深拷贝浅拷贝（Shal
数字里的世界17期：2021年全球10大顶级数据中心，中国移动榜首张三叨
你知道吗？2016年，全球的数据中心共计用电4160亿千瓦时，比整个英国的发电量还多40％！前言每天，我们都会创造超过250万TB的数据。并且随着物联网（IOT）的不断普及，这一数据将持续增长。如此庞大的数据被存储在被称为“数据中心”的专用设施中。虽然最早的数据中心建于20世纪40年代，但直到1997-2000年的互联网泡沫期间才逐渐成为主流。当前人类的技术，比如人工智能和机器学习，已经将我们推向
nosql数据库技术与应用知识点皆过客，揽星河 NoSQL nosql 数据库大数据数据分析数据结构非关系型数据库
Nosql知识回顾大数据处理流程数据采集(flume、爬虫、传感器)数据存储(本门课程NoSQL所处的阶段)Hdfs、MongoDB、HBase等数据清洗(入仓)Hive等数据处理、分析(Spark、Flink等)数据可视化数据挖掘、机器学习应用(Python、SparkMLlib等)大数据时代存储的挑战(三高)高并发(同一时间很多人访问)高扩展(要求随时根据需求扩展存储)高效率(要求读写速度快)
《Python数据分析实战终极指南》 xjt921122 python 数据分析开发语言
对于分析师来说，大家在学习Python数据分析的路上，多多少少都遇到过很多大坑**，有关于技能和思维的**：Excel已经没办法处理现有的数据量了，应该学Python吗？找了一大堆Python和Pandas的资料来学习，为什么自己动手就懵了？跟着比赛类公开数据分析案例练了很久，为什么当自己面对数据需求还是只会数据处理而没有分析思路？学了对比、细分、聚类分析，也会用PEST、波特五力这类分析法，为啥
Python中深拷贝与浅拷贝的区别 yuxiaoyu.
转自：http://blog.csdn.net/u014745194/article/details/70271868定义：在Python中对象的赋值其实就是对象的引用。当创建一个对象，把它赋值给另一个变量的时候，python并没有拷贝这个对象，只是拷贝了这个对象的引用而已。浅拷贝：拷贝了最外围的对象本身，内部的元素都只是拷贝了一个引用而已。也就是，把对象复制一遍，但是该对象中引用的其他对象我不复
Python开发常用的三方模块如下：换个网名有点难 python 开发语言
Python是一门功能强大的编程语言，拥有丰富的第三方库，这些库为开发者提供了极大的便利。以下是100个常用的Python库，涵盖了多个领域：1、NumPy，用于科学计算的基础库。2、Pandas，提供数据结构和数据分析工具。3、Matplotlib，一个绘图库。4、Scikit-learn，机器学习库。5、SciPy，用于数学、科学和工程的库。6、TensorFlow，由Google开发的开源机
Python编译器鹿鹿~ Python编译器 Python python 开发语言后端
嘿嘿嘿我又来了啊有些小盆友可能不知道Python其实是有编译器的，也就是PyCharm。你们可能会问到这个是干嘛的又不可以吃也不可以穿好像没有什么用，其实你还说对了这个还真的不可以吃也不可以穿，但是它用来干嘛的呢。用来编译你所打出的代码进行运行（可能这里说的有点不对但是只是个人认为）现在我们来说说PyCharm是用来干嘛的。PyCharm是一种PythonIDE，带有一整套可以帮助用户在使用Pyt
JAVA中的Enum 周凡杨 java enum 枚举
Enum是计算机编程语言中的一种数据类型---枚举类型。在实际问题中，有些变量的取值被限定在一个有限的范围内。例如，一个星期内只有七天我们通常这样实现上面的定义： public String monday; public String tuesday; public String wensday; public String thursday
赶集网mysql开发36条军规 Bill_chen mysql 业务架构设计 mysql调优 mysql性能优化
(一)核心军规 (1)不在数据库做运算 cpu计算务必移至业务层； (2)控制单表数据量 int型不超过1000w，含char则不超过500w；合理分表；限制单库表数量在300以内； (3)控制列数量字段少而精，字段数建议在20以内
Shell test命令 daizj shell 字符串 test 数字文件比较
Shell test命令 Shell中的 test 命令用于检查某个条件是否成立，它可以进行数值、字符和文件三个方面的测试。数值测试参数说明 -eq 等于则为真 -ne 不等于则为真 -gt 大于则为真 -ge 大于等于则为真 -lt 小于则为真 -le 小于等于则为真实例演示： num1=100 num2=100if test $[num1]
XFire框架实现WebService(二) 周凡杨 java webservice
有了XFire框架实现WebService(一)，就可以继续开发WebService的简单应用。 Webservice的服务端(WEB工程)：两个java bean类： Course.java package cn.com.bean; public class Course { private
重绘之画图板朱辉辉33 画图板
上次博客讲的五子棋重绘比较简单，因为只要在重写系统重绘方法paint（）时加入棋盘和棋子的绘制。这次我想说说画图板的重绘。画图板重绘难在需要重绘的类型很多，比如说里面有矩形，园，直线之类的，所以我们要想办法将里面的图形加入一个队列中，这样在重绘时就
Java的IO流西蜀石兰 java
刚学Java的IO流时，被各种inputStream流弄的很迷糊，看老罗视频时说想象成插在文件上的一根管道，当初听时觉得自己很明白，可到自己用时，有不知道怎么代码了。。。每当遇到这种问题时，我习惯性的从头开始理逻辑，会问自己一些很简单的问题，把这些简单的问题想明白了，再看代码时才不会迷糊。 IO流作用是什么？答：实现对文件的读写，这里的文件是广义的； Java如何实现程序到文件
No matching PlatformTransactionManager bean found for qualifier 'add' - neither 林鹤霄
java.lang.IllegalStateException: No matching PlatformTransactionManager bean found for qualifier 'add' - neither qualifier match nor bean name match! 网上找了好多的资料没能解决，后来发现：项目中使用的是xml配置的方式配置事务，但是
Row size too large (> 8126). Changing some columns to TEXT or BLOB aigo column
原文：http://stackoverflow.com/questions/15585602/change-limit-for-mysql-row-size-too-large 异常信息： Row size too large (> 8126). Changing some columns to TEXT or BLOB or using ROW_FORMAT=DYNAM
JS 格式化时间 alxw4616 JavaScript
/** * 格式化时间 2013/6/13 by 半仙 [email protected] * 需要 pad 函数 * 接收可用的时间值. * 返回替换时间占位符后的字符串 * * 时间占位符:年 Y 月 M 日 D 小时 h 分 m 秒 s 重复次数表示占位数 * 如 YYYY 4占4位 YY 占2位<p></p> * MM DD hh mm
队列中数据的移除问题百合不是茶队列移除
队列的移除一般都是使用的remov();都可以移除的,但是在昨天做线程移除的时候出现了点问题,没有将遍历出来的全部移除, 代码如下; // package com.Thread0715.com; import java.util.ArrayList; public class Threa
Runnable接口使用实例 bijian1013 java thread Runnable java多线程
Runnable接口 a. 该接口只有一个方法：public void run(); b. 实现该接口的类必须覆盖该run方法 c. 实现了Runnable接口的类并不具有任何天
oracle里的extend详解 bijian1013 oracle 数据库 extend
扩展已知的数组空间，例： DECLARE TYPE CourseList IS TABLE OF VARCHAR2(10); courses CourseList; BEGIN -- 初始化数组元素，大小为3 courses := CourseList('Biol 4412 ', 'Psyc 3112 ', 'Anth 3001 '); --
【httpclient】httpclient发送表单POST请求 bit1129 httpclient
浏览器Form Post请求浏览器可以通过提交表单的方式向服务器发起POST请求，这种形式的POST请求不同于一般的POST请求 1. 一般的POST请求，将请求数据放置于请求体中，服务器端以二进制流的方式读取数据，HttpServletRequest.getInputStream()。这种方式的请求可以处理任意数据形式的POST请求，比如请求数据是字符串或者是二进制数据 2. Form
【Hive十三】Hive读写Avro格式的数据 bit1129 hive
1. 原始数据 hive> select * from word; OK 1 MSN 10 QQ 100 Gtalk 1000 Skype 2. 创建avro格式的数据表 hive> CREATE TABLE avro_table(age INT, name STRING)STORE
nginx+lua+redis自动识别封解禁频繁访问IP ronin47
在站点遇到攻击且无明显攻击特征，造成站点访问慢，nginx不断返回502等错误时，可利用nginx+lua+redis实现在指定的时间段内，若单IP的请求量达到指定的数量后对该IP进行封禁，nginx返回403禁止访问。利用redis的expire命令设置封禁IP的过期时间达到在指定的封禁时间后实行自动解封的目的。一、安装环境： CentOS x64 release 6.4(Fin
java-二叉树的遍历-先序、中序、后序（递归和非递归）、层次遍历 bylijinnan java
import java.util.LinkedList; import java.util.List; import java.util.Stack; public class BinTreeTraverse { //private int[] array={ 1, 2, 3, 4, 5, 6, 7, 8, 9 }; private int[] array={ 10,6,
Spring源码学习-XML 配置方式的IoC容器启动过程分析 bylijinnan java spring IOC
以FileSystemXmlApplicationContext为例，把Spring IoC容器的初始化流程走一遍： ApplicationContext context = new FileSystemXmlApplicationContext ("C:/Users/ZARA/workspace/HelloSpring/src/Beans.xml&q
[科研与项目]民营企业请慎重参与军事科技工程 comsci 企业
军事科研工程和项目并非要用最先进，最时髦的技术，而是要做到“万无一失” 而民营科技企业在搞科技创新工程的时候，往往考虑的是技术的先进性，而对先进技术带来的风险考虑得不够，在今天提倡军民融合发展的大环境下，这种“万无一失”和“时髦性”的矛盾会日益凸显。。。。。。所以请大家在参与任何重大的军事和政府项目之前，对
spring 定时器-两种方式 cuityang spring quartz 定时器
方式一：间隔一定时间运行 <bean id="updateSessionIdTask" class="com.yang.iprms.common.UpdateSessionTask" autowire="byName" /> <bean id="updateSessionIdSchedule
简述一下关于BroadView站点的相关设计 damoqiongqiu view
终于弄上线了，累趴，戳这里http://www.broadview.com.cn 简述一下相关的技术点前端：jQuery+BootStrap3.2+HandleBars，全站Ajax（貌似对SEO的影响很大啊！怎么破？），用Grunt对全部JS做了压缩处理，对部分JS和CSS做了合并（模块间存在很多依赖，全部合并比较繁琐，待完善）。后端：U
运维 PHP问题汇总 dcj3sjt126com windows2003
1、Dede(织梦)发表文章时,内容自动添加关键字显示空白页解决方法：后台>系统>系统基本参数>核心设置>关键字替换（是/否），这里选择“是”。后台>系统>系统基本参数>其他选项>自动提取关键字，这里选择“是”。 2、解决PHP168超级管理员上传图片提示你的空间不足网站是用PHP168做的，反映使用管理员在后台无法
mac 下安装php扩展 - mcrypt dcj3sjt126com PHP
MCrypt是一个功能强大的加密算法扩展库，它包括有22种算法，phpMyAdmin依赖这个PHP扩展，具体如下：下载并解压libmcrypt-2.5.8.tar.gz。在终端执行如下命令： tar zxvf libmcrypt-2.5.8.tar.gz cd libmcrypt-2.5.8/ ./configure --disable-posix-threads --
MongoDB更新文档 [四] eksliang mongodb Mongodb更新文档
MongoDB更新文档转载请出自出处：http://eksliang.iteye.com/blog/2174104 MongoDB对文档的CURD，前面的博客简单介绍了，但是对文档更新篇幅比较大，所以这里单独拿出来。语法结构如下： db.collection.update( criteria, objNew, upsert, multi) 参数含义参数
Linux下的解压，移除，复制，查看tomcat命令 y806839048 tomcat
重复myeclipse生成webservice有问题删除以前的，干净 1、先切换到：cd usr/local/tomcat5/logs 2、tail -f catalina.out 3、这样运行时就可以实时查看运行日志了 Ctrl+c 是退出tail命令。有问题不明的先注掉 cp /opt/tomcat-6.0.44/webapps/g
Spring之使用事务缘由(3-XML实现) ihuning spring
用事务通知声明式地管理事务事务管理是一种横切关注点。为了在 Spring 2.x 中启用声明式事务管理，可以通过 tx Schema 中定义的 <tx:advice> 元素声明事务通知，为此必须事先将这个 Schema 定义添加到 <beans> 根元素中去。声明了事务通知后，就需要将它与切入点关联起来。由于事务通知是在 <aop:
GCD使用经验与技巧浅谈啸笑天 GC
前言 GCD(Grand Central Dispatch)可以说是Mac、iOS开发中的一大“利器”，本文就总结一些有关使用GCD的经验与技巧。 dispatch_once_t必须是全局或static变量这一条算是“老生常谈”了，但我认为还是有必要强调一次，毕竟非全局或非static的dispatch_once_t变量在使用时会导致非常不好排查的bug，正确的如下： 1
linux（Ubuntu）下常用命令备忘录1 macroli linux 工作 ubuntu
在使用下面的命令是可以通过--help来获取更多的信息1,查询当前目录文件列表：ls ls命令默认状态下将按首字母升序列出你当前文件夹下面的所有内容，但这样直接运行所得到的信息也是比较少的，通常它可以结合以下这些参数运行以查询更多的信息： ls / 显示/.下的所有文件和目录 ls -l 给出文件或者文件夹的详细信息 ls -a 显示所有文件，包括隐藏文
nodejs同步操作mysql qiaolevip 学习永无止境每天进步一点点 mysql nodejs
// db-util.js var mysql = require('mysql'); var pool = mysql.createPool({ connectionLimit : 10, host: 'localhost', user: 'root', password: '', database: 'test', port: 3306 });
一起学Hive系列文章 superlxw1234 hive Hive入门
[一起学Hive]系列文章目录贴，入门Hive，持续更新中。 [一起学Hive]之一—Hive概述，Hive是什么 [一起学Hive]之二—Hive函数大全-完整版 [一起学Hive]之三—Hive中的数据库(Database)和表(Table) [一起学Hive]之四-Hive的安装配置 [一起学Hive]之五-Hive的视图和分区 [一起学Hive
Spring开发利器：Spring Tool Suite 3.7.0 发布 wiselyman spring
Spring Tool Suite(简称STS)是基于Eclipse，专门针对Spring开发者提供大量的便捷功能的优秀开发工具。在3.7.0版本主要做了如下的更新：将eclipse版本更新至Eclipse Mars 4.5 GA Spring Boot(JavaEE开发的颠覆者集大成者，推荐大家学习)的配置语言YAML编辑器的支持(包含自动提示，

SHAP（六）：使用 XGBoost 和 HyperOpt 进行信用卡欺诈检测