13 Red-black Trees
13 Red-black Trees
Red-black trees are one of many search-tree schemes that are "balanced" in order to guarantee that basic dynamic-set operations take O(lgn) time in the worst case.
Red-black trees 是许多搜索树框架中得一个。这些树为了保证基本的动态集合在最坏情况下操作时间在0(lgn ),采取了自平衡。
A red-black tree is a binary tree that satisfies the following red-black properties:
1. Every node is either red or black.
2. The root is black.
3. Every leaf (NIL) is black.
4. If a node is red, then both its children are black.
5. For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.
1 所有的节点非红即黑
2 根是黑的
3 叶子(Nil)也是黑得
4 一个节点是红得,孩子必定是黑的。
5 对于每个节点,从这个节点到叶子的任意路径包含同样数量的黑的。
red-black tree 的属性从2-5感觉都是针对黑色的限制。
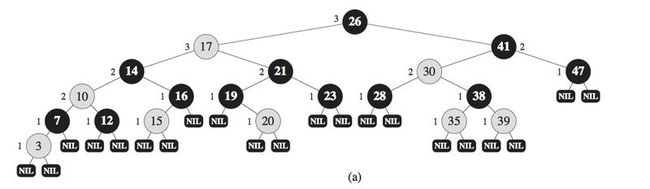
an example of a red-black tree.
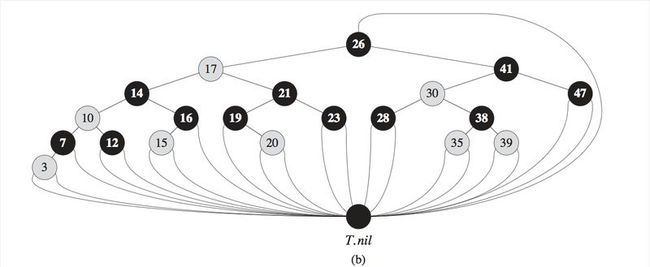
As a matter of convenience in dealing with boundary conditions in red-black
tree code, we use a single sentinel to represent NIL
All pointers to NIL are replaced by pointers to the sentinel T.nil
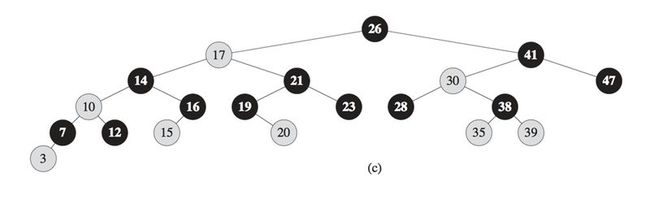
In the remainder of this chapter, we omit the leaves when we draw red-black trees, as shown
We call the number of black nodes on any simple path from, but not including, a node x down to a leaf the black-height of the node, denoted bh(x)
13.2 Rotations
We change the pointer structure through rotation, which is a local operation in a search tree that preserves the binary-search-tree property.
我们通过rotation来改变指针结构。它是保留搜索树属性的一个本地操作。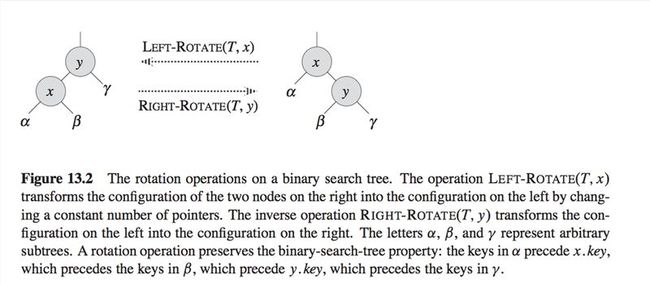
13.3 Insertion
We can insert a node into an n-node red-black tree in O(lgn) time.
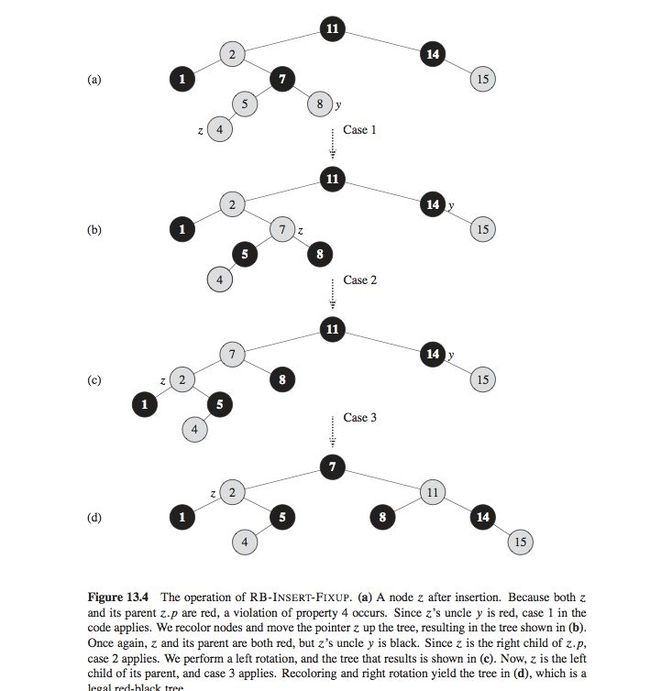
To do so, we use a slightly modified version of the TREE-INSERT procedure (Section 12.3) to insert node ́ into the tree T as if it were an ordinary binary search tree, and then we color z red.
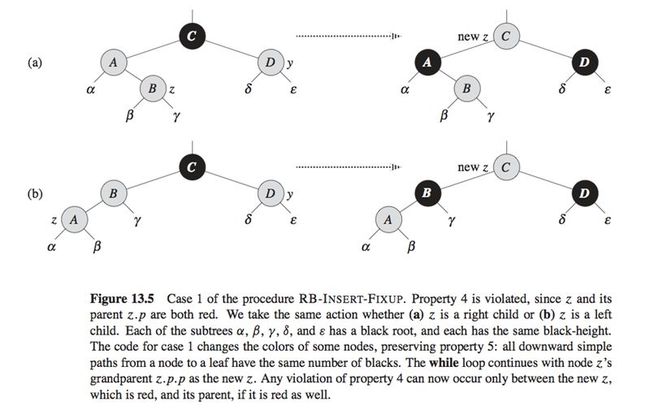
Case1:
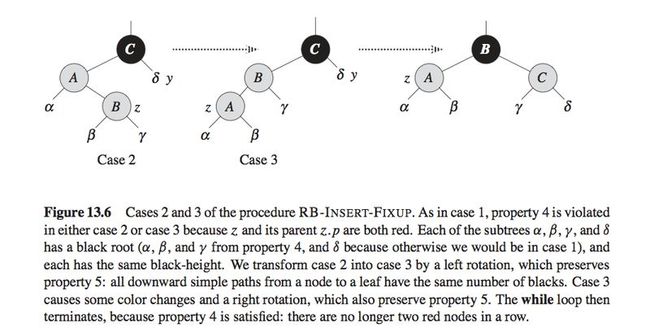
Case 2 and case 3
13.4 Deletion
Like the other basic operations on an n-node red-black tree, deletion of a node takes time O(lgn ). Deleting a node from a red-black tree is a bit more complicated than inserting a node .
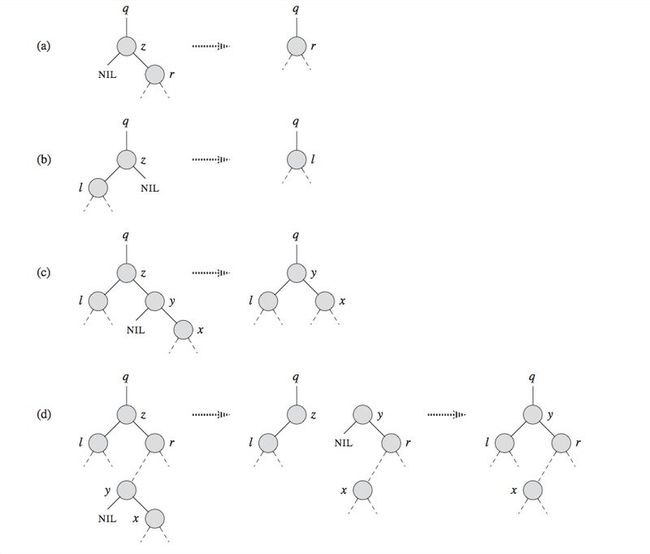
First ,we need to customize the TRANSPLANT subroutine that Tree-Delete calls so that it applies to a red-black tree :
Here is the red-black delete tree program :
Finally, if node y was black, we might have introduced one or more violations of the red-black properties, and so we call RB-DELETE-FIXUP in line 22 to restore the red-black properties. If y was red, the red-black properties still hold when y is removed or moved, for the following reasons:
如果节点y是黑色的,我们可能引入一个或多个违反红黑树性质。如果y是红色的,则红黑树的性质能得到保证。原因如下:
1. No black-heights in the tree have changed.
黑色深度没有变化
2. No red nodes have been made adjacent. Because y takes z's place in the tree, along with z's color, we cannot have two adjacent red nodes at y's new position in the tree. In addition, if y was not ́'s right child, then y's original right child x replaces y in the tree. If y is red, then x must be black, and so replacing y by x cannot cause two red nodes to become adjacent.
没有红色节点相邻。因为y取代了z得位置,并且取得了z得颜色,z原来是具有红黑树属性的,所以替换了以后仍然有。
另外,如果y不是z的右孩子,则y的原来位置被x取代了。如果y是红色的话,那么x肯定是黑色的,所以被x取代y 不可能导致两个红色节点相邻。
3. Since y could not have been the root if it was red, the root remains black.
如果y是红色的话,y肯定不是根,因此根仍然保持黑色。
If node y was black, three problems may arise, which the call of RB-DELETE- FIXUP will remedy.
First, if y had been the root and a red child of y becomes the new root, we have violated property 2.
首先如果y是根,并且y的一个红孩子成为了新根,那么违反 根是黑色的 属性。
Second, if both x and x.p are red, then we have violated property 4.
如果x和x.p 是红色的,那么我们可能违反 红色节点不能相邻这一条。
Third, moving y within the tree causes any simple path that previously contained y to have one fewer black node. Thus, property 5 is now violated by any ancestor of y in the tree.
第三,如果移动y,那么任意一条原先包含y的路线可能比其他的路线少一条黑色,因此,从任意一节点到叶子的黑色节点数是相同的。
We can correct the violation of property 5 by saying that node x, now occupying y's original position, has an "extra" black.
我们可以纠正 第五条属性 通过将现在占据y的原来位置的x的属性 有一个额外的黑色。
That is, if we add 1 to the count of black nodes on any simple path that contains x, then under this interpretation, property 5 holds.
也就是说,在我们计算从任意一条包括x节点的简单路径的时候,多增加1就能保持 属性5 。
When we remove or move the black node y, we "push" its blackness onto node x.
当我们移动黑色节点y时,我们将她的黑色推到节点x上。
The problem is that now node x is neither red nor black, thereby violating property 1.
现在问题是现在的节点x既不是黑色也不是红色,违反了属性1.
Instead,node x is either "doubly black" or "red-and-black," and it contributes either 2 or 1, respectively, to the count of black nodes on simple paths containing x.
节点x是双黑,或红黑,在计算包含x的简单路径上它将分别贡献一个或两个。
The color attribute of x will still be either RED (if x is red-and-black) or BLACK (if x is doubly black).
x的属相将仍然是红色(如果x是红黑)或黑色(如果x是双黑)。
In other words, the extra black on a node is reflected in x's pointing to the node rather than in the color attribute.
换句话说,一个节点的额外的黑色反应了x得位置而非颜色属性。
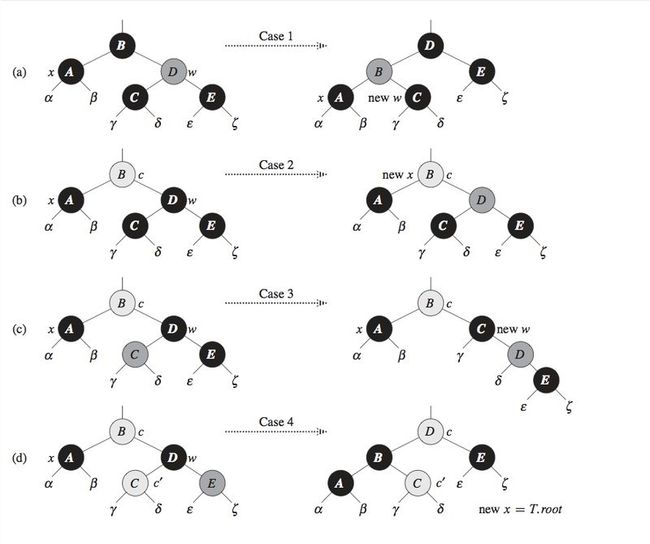
Case1: x'sibling w is red
通过转化,转换成Case2,3,4 的任意一种
Case2 :x's sibling w is black ,and both of w's children are black
即x的兄弟,还有兄弟的孩子都是黑色,则让x的兄弟便红,x转移到x得父节点
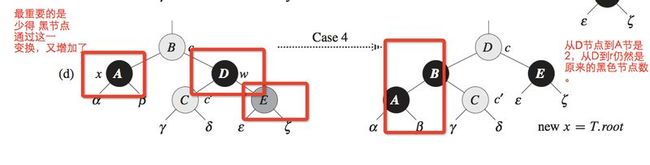
Case3:x的兄弟是黑色,兄弟的右孩子是红色。则通过转换,转换成Case4
Case4:x的兄弟是黑色,兄弟的左孩子是红色。这个就可以解决黑色节点的问题。