生存分析KM与cox
生存分析(survival analysis)是研究生存时间和结局事件的分布及其影响因素的统计方法。在生存分析中,生存函数(survival function)S(I)用于刻画某个时刻t的研究对象存活的概率,风险函数(hazard function)h(A)用于度量在某个时刻t还存活的个体在极短的时间内死亡的风险。
删失点:对于随访结束没有发生结局事件的研究对象,最后的状态称为“删失”(censoring)。例如在癌症治疗的试验中,有些患者失去了联系,或者他们的生存时间长于试验的研究期,这时我们无法获得这部分患者真正的生存时间。这种删失叫右删失(rightcensoring),在生存分析中是最常见的。此外还有左删失(left censoring),指生存时间小于某一时间段;区间删失(interval censoring),指生存时间在某一段时间之内。如果在分析中忽略删失数据,将很可能得到偏倚的结果。
生存对象
在生存分析中,每个研究对象的结局变量由“time”(时间)和“event”(事件)组成。若用数字表示,结局事件发生为1,否则为0。在survival包中用函数Surv()生成,它是将生存时间(time)和事件(event)合并在一起的一种数据结构。
rm(list = ls())
library(survival)
library(survminer)
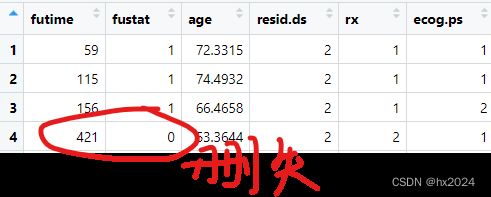
ovarian <- ovarianfutime随访时间;变量fustat是患者在研究截止时的状态:0表示存活,1表示死亡。其他变量包括age(患者的年龄)、resid.ds(疾病残留情况:1表示没有残留,2表示有残留)、rx(治疗方法:1表示环磷酰胺,2表示环磷酰胺加阿霉素)和ecog.ps(患者的ECOG评分:1表示较好,2表示较差)。
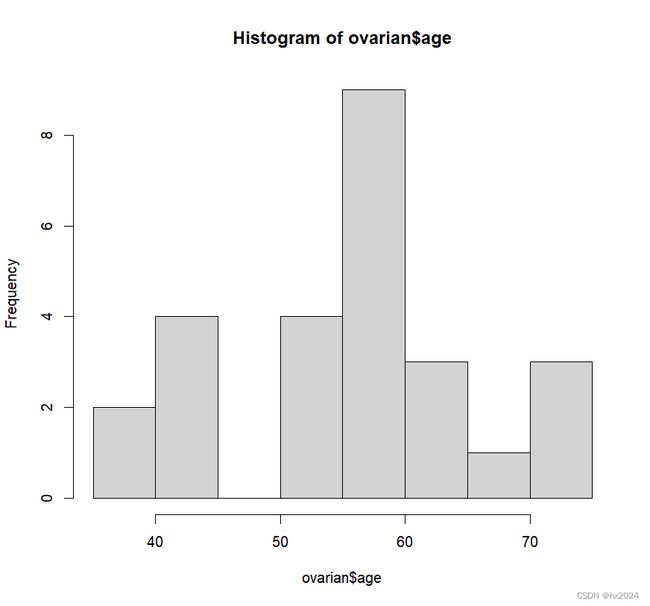
注意 hist(ovarian$age)##年龄的分布不是对称的。考虑到结果的易解释性,这里把变量age转换成因子。
对象查看:
##年龄转换为因子
ovarian$agegr <- cut(ovarian$age,
breaks=c(0,50,75),
labels = c("<=50",">50"))#以50 分界
surv1 <- Surv(time =ovarian$futime,event =ovarian$fustat )
surv1
[1] 59 115 156 421+ 431 448+ 464 475 477+ 563 638 744+
[13] 769+ 770+ 803+ 855+ 1040+ 1106+ 1129+ 1206+ 1227+ 268 329 353
[25] 365 377+解释:“+”号表示删失数据。例如,第4个值“421+”表示这个患者并未在421天死于卵巢癌,只是没有继续随访(可能是由于研究结束、失访、死于其他原因等)。
KM
生存率估计
surv1 <- Surv(time =ovarian$futime,event =ovarian$fustat )
surv1
##KM 生存率估计与生存曲线
survfit(surv1~1)#没有自变量的情况下
Call: survfit(formula = surv1 ~ 1)
n events median 0.95LCL 0.95UCL
[1,] 26 12 638 464 NA
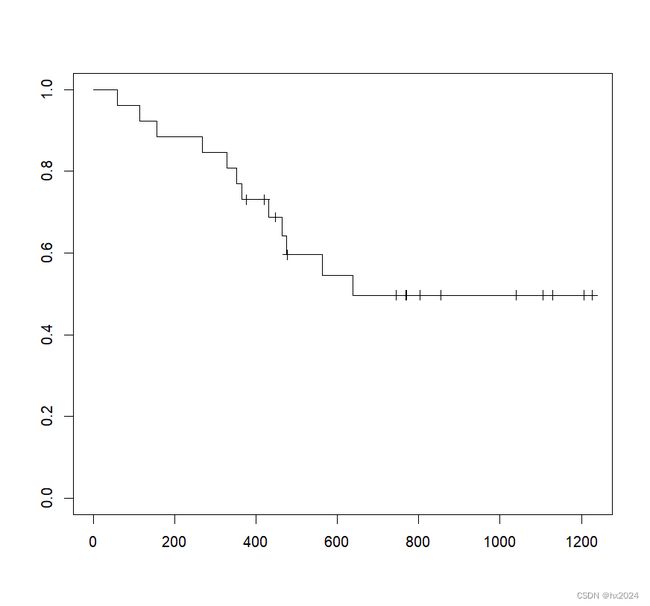
plot(surv1,mark.time=T,conf.int=F)删失数据为“+”
生存率比较
可以通过在函数survfit()的公式中增加一个因子变量来获得该变量不同水平下的生存信息。
survrx <- survfit(surv1~rx,data = ovarian)
summary(survrx)#结果查看
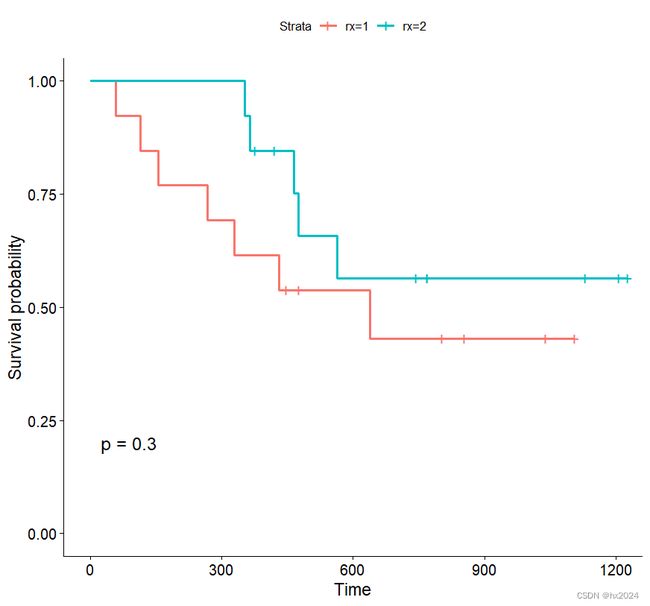
ggsurvplot(survrx,data =ovarian,pval = T )时序检验(log rank test)
治疗方法“2”(环磷酰胺加阿霉素)的生存率高于治疗方法“1”(环磷酰胺)。但这种差异是偶然的还是由治疗方法的不同引起的,需要进行统计学检验。其中最常用的是时序检验(log rank test),其基本思想是先计算出不同时间两种治疗方法的暴露人数和死亡人数,并由此在两种治疗方法效果相同的假设下计算出期望死亡人数,如果不拒绝零假设,则实际观测值和期望值的差异不会很大,如果差异过大则不能认为是由随机误差引起的差异。对此,用 检验作判断。时序检验可以用函数survdiff()来实现。
##查看log rank P
survdiff(surv1~rx,data = ovarian)
Call:
survdiff(formula = surv1 ~ rx, data = ovarian)
N Observed Expected (O-E)^2/E (O-E)^2/V
rx=1 13 7 5.23 0.596 1.06
rx=2 13 5 6.77 0.461 1.06
Chisq= 1.1 on 1 degrees of freedom, p= 0.3 COX
cox回归模型
rm(list = ls())
library(survival)
library(survminer)
ovarian <- ovarian
ovarian$agegr <- cut(ovarian$age,
breaks=c(0,50,75),
labels = c("<=50",">50"))#以50 分界
surv1 <- Surv(time =ovarian$futime,event =ovarian$fustat )
cox1 <- coxph(surv1~rx+resid.ds+agegr+ecog.ps,#cox分析对象
data = ovarian)
summary(cox1)Call:
coxph(formula = surv1 ~ rx + resid.ds + agegr + ecog.ps, data = ovarian)
n= 26, number of events= 12
coef exp(coef) se(coef) z Pr(>|z|)
rx -1.3814 0.2512 0.6448 -2.142 0.0322 *
resid.ds 1.4470 4.2503 0.7292 1.984 0.0472 *
agegr>50 2.2013 9.0368 1.1069 1.989 0.0467 *
ecog.ps 0.5859 1.7966 0.6329 0.926 0.3546
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
exp(coef) exp(-coef) lower .95 upper .95
rx 0.2512 3.9803 0.0710 0.8891
resid.ds 4.2503 0.2353 1.0180 17.7453
agegr>50 9.0368 0.1107 1.0324 79.1031
ecog.ps 1.7966 0.5566 0.5197 6.2113
Concordance= 0.782 (se = 0.065 )
Likelihood ratio test= 12.19 on 4 df, p=0.02
Wald test = 9.02 on 4 df, p=0.06
Score (logrank) test = 11.97 on 4 df, p=0.02
结果表明在多变量cox分析模型中:rx治疗方法有生存差异
进行多变量的选择
drop1(cox1,test ="Chisq")Single term deletions
Model:
surv1 ~ rx + resid.ds + agegr + ecog.ps
Df AIC LRT Pr(>Chi)
65.775
rx 1 68.489 4.7134 0.02993 *
resid.ds 1 68.377 4.6016 0.03194 *
agegr 1 69.939 6.1641 0.01304 *
ecog.ps 1 64.658 0.8828 0.34744 ##需要去除
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
step()基于AIC值进行变量选择
step.cox <- step(cox1)
选择AIC值最小的模型(这个模型里也没有ecog.ps )
surv1 ~ rx + resid.ds + agegr
Df AIC
64.658
- resid.ds 1 66.452
- rx 1 66.945
- agegr 1 68.537
R语言生存分析:Cox回归_r语言cox回归分析_医学和生信笔记的博客-CSDN博客
用更简单的方式画森林图_add_underline属于哪个r包-CSDN博客