A comprehensive study of non-adaptive and residual-based adaptive sampling
论文阅读:A comprehensive study of non-adaptive and residual-based adaptive sampling for physics-informed neural networks
- A comprehensive study of non-adaptive and residual-based adaptive sampling for physics-informed neural networks
-
- 简介
- 各种采样方法
-
- 均匀分布的非适应性采样
- 非均匀自适应采样
-
- 基于残差的贪婪的自适应细化RAR-G
- 基于残差的适应性分布(RAD)
- 基于残差的自适应细化与分布(RAR-D)
- 实验比较
-
- 结论
- 正问题
- 反问题
- 建议
- 展望
- 总结
A comprehensive study of non-adaptive and residual-based adaptive sampling for physics-informed neural networks
简介
在监督学习中,数据集在训练期间是固定的,但在PINNs中,我们可以在任何位置选择残差点。因此,在每次优化迭代中,我们可以选择一组新的残差点,而不是在训练期间使用相同的残差点,这一点在DeepXDE中首次强调。虽然这种策略已经在一些工作中使用,但它还没有被系统地测试。
作者广泛地比较了不同的均匀采样方法的性能,包括:
- 等距均匀网格;
- 均匀随机采样;
- LHS;
- Sobol序列;
- Halton序列;
- Hammersley序列。
并测试了多种重采样策略的性能,并首次研究了残差点的数量和重采样范围的影响,包括:
- 基于均匀点的重采样(Random-R);
- 基于残差的贪婪的自适应细化(RAR-G);
- 基于残差的适应性分布(RAD);
- 基于残差的自适应细化与分布(RAR-D)。
各种采样方法
均匀分布的非适应性采样
-
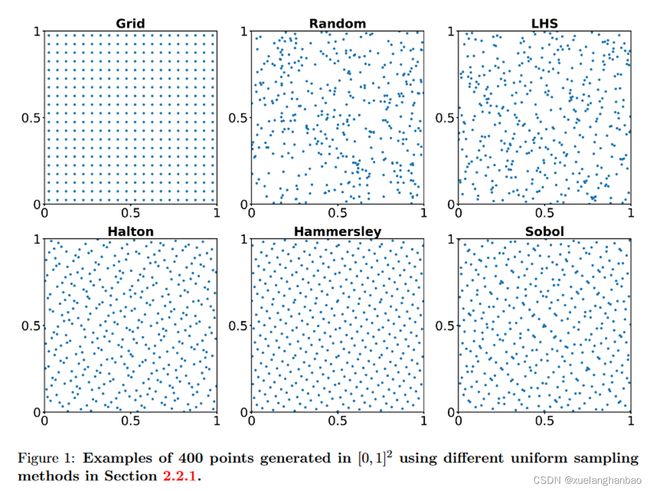
**等距均匀网格(Grid):**残差点被选为计算域的等距均匀网格的节点;
-
**均匀随机采样(Random):**残差点是根据域上的连续均匀分布随机采样的。在实践中,这通常是使用伪随机数生成器来完成的,如PCG-64算法;
-
**拉丁超立方体采样(LHS):**LHS是一种分层的蒙特卡洛采样方法,它可以在概率相等的基础上产生间隔内的随机样本,并且每个范围都服从正态分布;
-
准随机低差异序列
-
哈尔顿序列(Halton):哈尔顿样本是根据使用素数的反转或翻转数字的基数转换而产生的;
-
哈默斯利序列(Hammersley):哈默斯利序列与哈尔顿序列相同,只是在第一维度上,点与点之间是等距的;
-
索博尔序列(Sobol):索博尔序列是一个基于2为底数的数字序列,以高度一致的方式进行填充。
-
-
**基于均匀点的重采样(Random-R):**在每次优化迭代中选择一组新的残差点。本文只考虑基于均匀随机采样的重采样
上图为使用不同均匀分布的非适应性采样算法在 [ 0 , 1 ] 2 [0,1]^2 [0,1]2 区域上采样400个点的结果
非均匀自适应采样
-
**基于残差的贪婪的自适应细化(RAR-G):**每一轮在PDE残差较大的位置添加新的点。RAR只关注有大残差的点,因此它是一个贪婪的算法;
-
**基于残差的适应性分布(RAD):**每一轮,根据所有的残差点的概率密度函数p(x)重新采样,概率密度函数p(x)与PDE残差成正比;
-
**基于残差的自适应细化与分布(RAR-D):**一种RAR-G和RAD的混合方法。RAR-G类似,每一轮向训练数据集添加新的点;与RAD类似,新的点是基于概率密度函数的采样。
基于残差的贪婪的自适应细化RAR-G
第一个用于PINN的自适应采样方法是DeepXDE中提出的基于残差的自适应细化方法(RAR)。
RAR的目的是在训练过程中通过在PDE残差较大的位置采样更多的点来改善残差点的分布。具体来说,在每一次迭代之后,RAR在PDE残差大的位置增加新的点。RAR只关注有大残差的点,因此它是一个贪婪的算法。为了更好地区别于其他抽样方法,本文中RAR方法被称为RAR-G。
基于残差的适应性分布(RAD)
Efficient training of physics‐informed neural networks via importance sampling 在文中提出根据与PDE残差成比例的概率密度函数p(x)重新采样。
p ( x ) ∝ ε ( x ) , i . e . , p ( x ) = ε ( x ) A , w h e r e A = ∫ Ω ε ( x ) d x p(\mathbf{x})\propto \varepsilon (\mathbf{x}),\quad \,\,\mathrm{i}.\mathrm{e}.,\quad p(\mathbf{x})=\frac{\varepsilon (\mathbf{x})}{A},\quad \,\,\mathrm{where}\,\,A=\int_{\varOmega}{\varepsilon (\mathbf{x})dx} p(x)∝ε(x),i.e.,p(x)=Aε(x),whereA=∫Ωε(x)dx
作者发现这种方法对某些PDEs是有效的,但它在某些情况下效果并不好。所以作者根据这一想法,提出了一个改进的版本,称为基于残差的适应性分布(RAD)方法
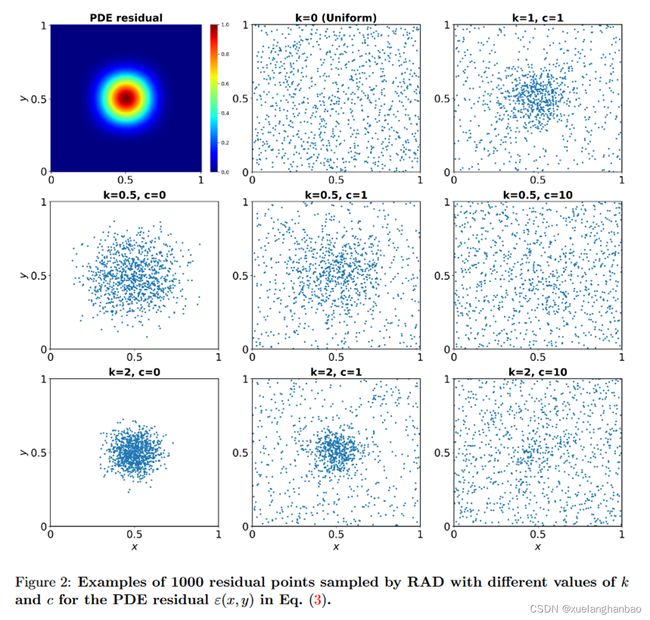
p ( x ) ∝ ε k ( x ) E [ ε k ( x ) ] + c p(\mathbf{x})\propto \frac{\varepsilon ^k(\mathbf{x})}{\mathbb{E} \left[ \varepsilon ^k(\mathbf{x}) \right]}+c p(x)∝E[εk(x)]εk(x)+c
其中 k k k 和 c c c 是控制采样分布的超参数。
上图就是对两个超参数的实验。左上角是残差的分布情况,中心残差最大,周围残差较小。可以看出, k k k 越大,对PDE 残差大的区域的采样就会更密集。 c c c 越大,采样就越均匀。
基于残差的自适应细化与分布(RAR-D)
作者还提出了一种RAR-G和RAD的混合方法,即基于残差的适应性细化(RAR-D)。与RAR-G类似,RAR-D反复向训练数据集添加新的点;与RAD类似,新的点是根据点的概率密度进行采样的。
实验比较
结论
实验数据比较多,因此先说结论:
-
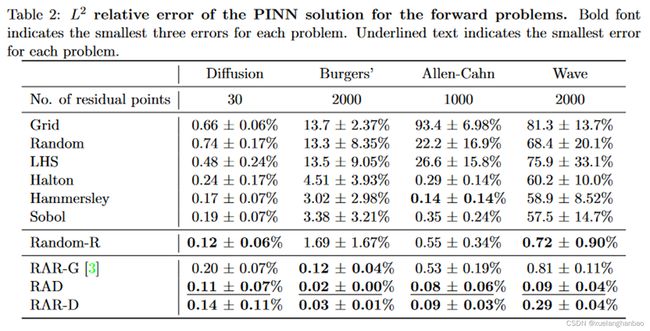
在所有的正向和反向问题中,RAD方法在10种采样方法中表现一直是最好的;
-
对于具有复杂解的PDEs,如Burgers和多尺度波方程,所提出的RAD和RAR-D方法是有效的,产生的误差幅度较低;
-
对于具有平滑解的PDEs,如扩散方程和扩散反应方程,一些均匀采样方法,如Hammersley和Random-R,也会产生足够低的误差;
-
与其他均匀采样方法相比,Random-R通常会表现出更好的性能;
-
在六种固定残差点的均匀采样方法中,低残差序列(Halton、Hammersley和Sobol)的表现普遍好于Random和LHS,而且都优于Grid。
正问题
作者在Diffusion、Burgers、Allen-Cahn和Wave四个正问题上进行了实验,每个用例都进行了10次训练,下文所有数据均为10次训练数据取平均值。
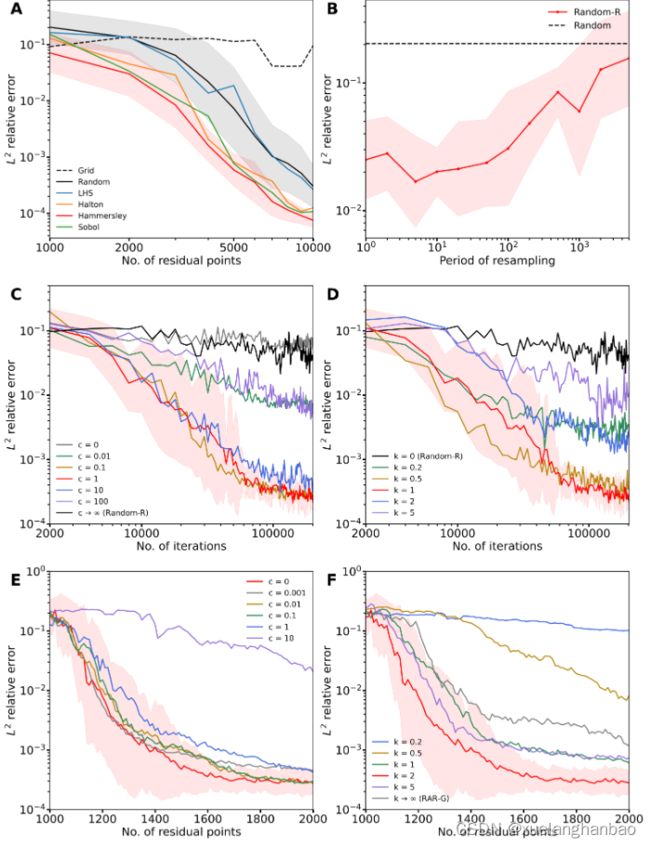
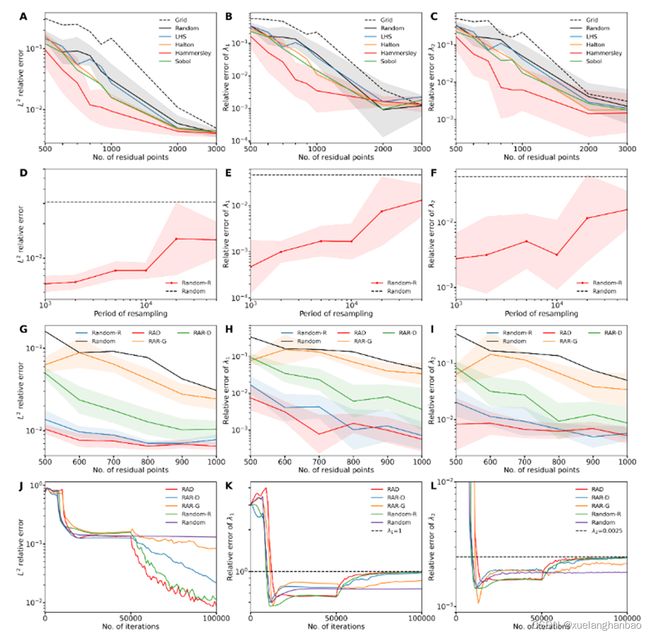
其中,Burgers方程的实验数据如下:
这里主要展示了 L 2 L^2 L2 误差随着训练的下降情况。其中图(A)展示了六种均匀分布的非适应性采样的结果;图(B)展示了使用Random-R算法周期性采样2000个残差点的结果;图(C)和图(D)展示了RAD算法在选择不同超参数后的结果,图(C)中 k = 1 k=1 k=1, 图(D)中 c = 1 c=1 c=1;图(E)和图(F)展示了RAR—D算法在选择不同超参数后的结果,图(E)中 k = 2 k=2 k=2, 图(F)中 c = 0 c=0 c=0。
更多实验数据请去查看原文。
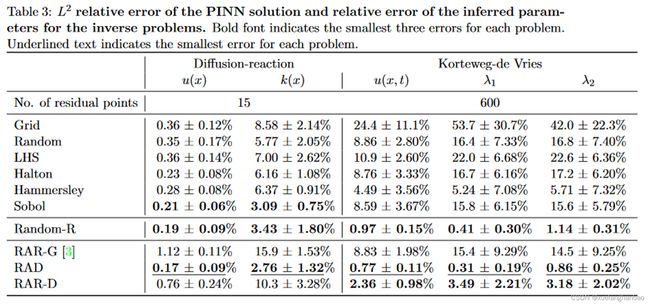
反问题
作者在Diffusion-reaction、和Korteweg-de Vries两个反问题上进行了实验,同样,每个用例都进行了10次训练,下文所有数据均为10次训练数据取平均值。
其中,Korteweg-de Vries方程的实验数据如下:
第一列是 L 2 L^2 L2 误差,第二三两列分别是参数 λ 1 \lambda_1 λ1 和 λ 2 \lambda_2 λ2 的相对误差。同样的,第一行展示了六种均匀分布的非适应性采样的结果;第二行展示了使用Random-R算法周期性采样1000个残差点的结果;第三行展示了Random、Random-R、RAD( k = 1 k = 1 k=1 和 c = 1 c = 1 c=1)、RAR-G 和 RAR-D( k = 2 k = 2 k=2 和 c = 0 c = 0 c=0)在不同残差点数量下的比较;第四行展示了在600个残差点下误差随训练过程的变化。
建议
根据上面实验结果得到的结论,作者总结了一些建议:
-
在解决一个新的PDE时,可以选择k=1和c=1的RAD作为默认的采样方法。可以对超参数k和c进行调整,以平衡具有不同PDE残差大小的位置上的点;
-
对于具有复杂解的PDEs,如Burgers和多尺度波方程,RAR-D可以达到与RAD相当的精度,但RAR-D的计算效率更高,因为它是逐渐增加残差点的数量。因此,在计算资源有限的情况下,RAR-D(默认情况下k=2,c=0)是比较好的;
-
在不允许自适应采样的情况下,可以使用Random-R,例如,很难根据概率密度函数对残差点进行采样。重新取样的周期不应选择太小或太大;
-
当我们必须使用一组固定的残差点时,例如在使用增强拉格朗日方法的PINNs(hPINNs)中,应该考虑低差异序列(例如哈默斯利),而不是网格、随机或LHS。
展望
在本文中,作者在RAD和RAR-D中通过使用直接抽样的方法对残差点进行采样,这种方法简单,容易实现,而且对许多PDEs来说是足够的。
然而,对于高维问题,我们需要使用其他方法,如逆变换采样、马尔科夫链蒙特卡洛算法以及生成对抗网络(GANs);
此外,采样点x的概率被认为是 p ( x ) ∝ ε k ( x ) E [ ε k ( x ) ] + c p(\mathbf{x})\propto \frac{\varepsilon ^k(\mathbf{x})}{\mathbb{E} \left[ \varepsilon ^k(\mathbf{x}) \right]}+c p(x)∝E[εk(x)]εk(x)+c 。虽然这个概率在本研究中非常好用,但有可能存在另一个更好的选择。我们可以通过元学习来学习一个新的概率密度函数。
总结
这篇文章比较了多种均匀分布及自适应采样方法,内容十分充实。
我之前看过Efficient training of physics‐informed neural networks via importance sampling这篇文章,但一直没能很好复现。本文作者将其中采样方法扩展后作为RAD方法,在所有任务上都展现出了良好的性能,其中对于超参数的选择也十分有趣。在RAD算法中, k = 1 , c = 1 k=1,c=1 k=1,c=1 表现出了比较好的性能,而在逐渐加点的RAR-D算法中, k = 2 , c = 0 k=2,c=0 k=2,c=0 则是更好的选择。不难理解,当每次替换所有残差点时,我们需要在低残差处也维持一定的残差点数量,使得网络能够在这些点处保持比较好的解;而当每次只是往训练集中加点时,由于训练集中已经有部分点处于低残差处,因此添加残差较大的训练点,就可以使网络在保持其他区域解的情况下,专注于优化这些残差较大处的解。
相关链接:
原文:A comprehensive study of non-adaptive and residual-based adaptive sampling for physics-informed neural networks - ScienceDirect
原文代码:lu-group/pinn-sampling: Non-adaptive and residual-based adaptive sampling for PINNs (github.com)