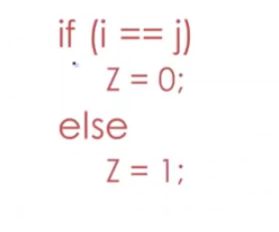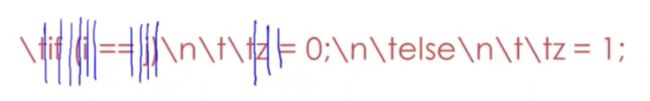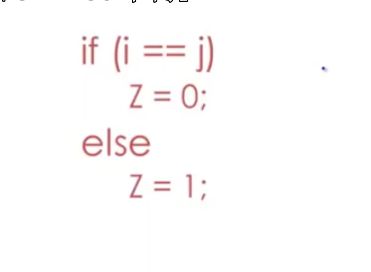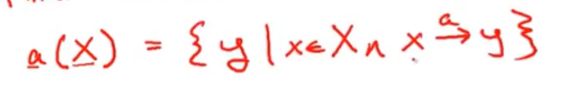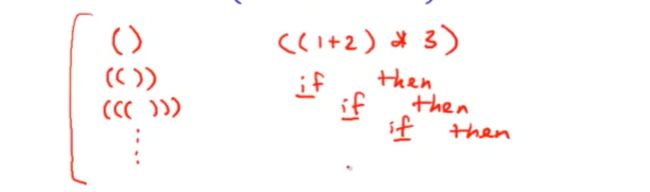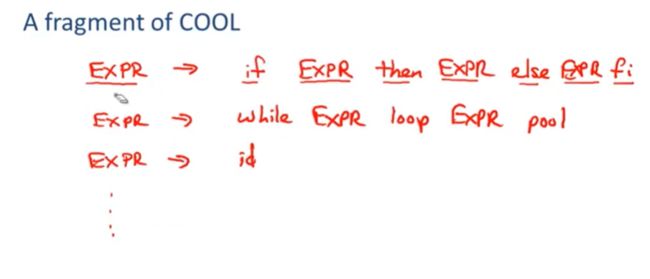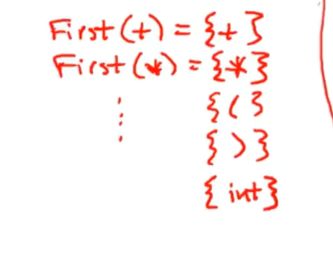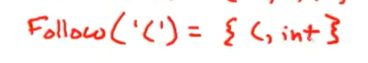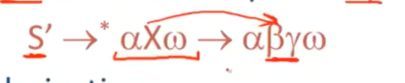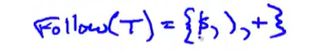编译原理 CS-143(更新至week4)
编译原理 CS-143
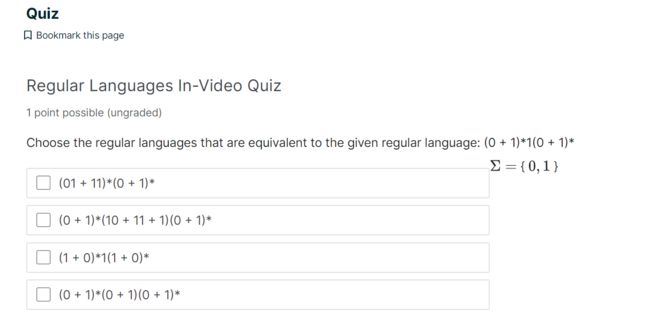
- Pre-Course Survey
-
- Navigation Your Course
- 01-01: Introduction (8m20s)
- 01-02: Structure of a Compiler (13m53s)【编译器结构】
-
- first step:recognize words
- 句法分析
- 句意分析
- optiimization(优化)
- finally code Gen
- 01-03: The Economy of Programming Languages (19m51s)【编译器性价比】
-
- why are there so many progamming languages
- why are there new programming languages?
- what is a good programming language?
- Summarize
- 02-01: Cool Overview (19m58s)【cool语言概述】
- 02-02: Cool Example II (15m04s)【cool样例2】
- 02-03: Cool Example III (18m05s)【cool样例3】
- CS-143 Week2 Lexical Analysis&Finite Automata[词法分析和有限自动机]
-
- 03-01: Lexical Analysis (12m06s)【词法分析】
-
- Token class(标记类)
- 样例分析
- Summarize
- Quiz
- 03-02: Lexical Analysis Examples (13m03s)【词法分析案例】
-
- 为什么需要lookahead
- PL/1 keywords are not reserved
- Summarize
- 03-03: Regular Languages Part 1 (11m48s)【正则语言part1】
-
- regular expressions 正则表达式
-
- 基本表达式
- 复合正则表达式
- example
- Quiz
- Summarize
- 03-04: Formal Languages (13m40s)【形式语言】
- 03-05: Lexical Specifications (16m19s)【词法规则】
-
- keyword
- integer
- identifier
- whitespace
- 课外example
- Summarize
- 04-01: Lexical Specification (14m30s)【词法规则2】
-
- 1.Write a rexp for the lexemes of each token class
- 2.Construct R,matching all lexemes for all tokens
- 3.Let input be x1...xn
- 4.if success ,then we know that
- 5.remove x1...xi from input and go to (3)
- question
- Summarize
- 04-02: Finite Automata Part 1 (13m01s)【有限自动机】
-
- Transition
- 另一种有限自动机的表达方式
- 编写 只接受数字1的自动机
- complex的例子
- Quiz
- DFA 和NFA
- 04-03: Regular Expressions into NFAs (9m41s)【从正则表达式到NFA】
-
- for each kind of rexp ,define an NFA
- 复杂的正则表示
- example
- quiz
- 04-04: NFA to DFA (15m12s)【从nfa到dfa】
-
- 任意的非确定性自动优先级映射到一个等效的确定性有限自动机
- example
- Quiz
- 04-05: Implementing Finite Automata (11m56s)【实现有限自动机】
-
- A DFA can be implemented by a 2D table T
- example
-
- 二维 表 2 dimension
- 一维表 1dimension
- NFA直接转换自动机
- summarize
- week2 Quiz
- CS-143 Week3 Parsing & Top-Down Parsing 【解析器&自顶向下的解析器】
-
- 05-01: Introduction to Parsing (5m31s) 【解释器介绍】
-
- parseing 可以做什么
- Summarize
- 05-02: Context Free Grammars Part 1 (12m38s)【上下文无关法】
-
- 上下文无关法的例子
- productions can be read as rules
-
- 1.begin with a string with only the start symbol S
- 2.replace any non-terminal X in the string by the right-hand side of some production X->Y1..Yn
- 3.repeat(2) until there are no non-terminals
- example
- finally
-
- terminal
- a fragment of cool
- some elements of the language
- simple arithmetic expression
- the idea of a CFG is a big step
- 05-03: Derivations Part 1 (7m07s)【推导】
-
- example
- parsing tree
- summarize
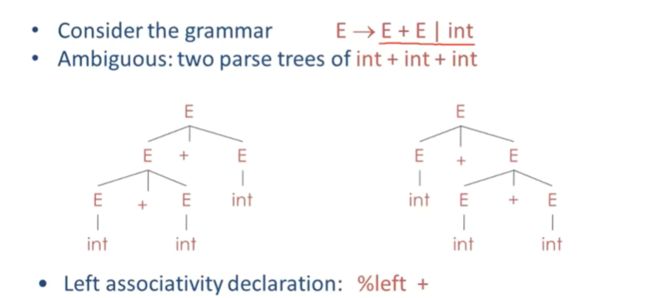
- 05-04: Ambiguity【歧义性】
-
- 消除歧义
- example
- 06-01: Error Handling (13m03s)【错误处理】
-
- 处理错误需要什么
- error handling
- panic example
-
- bsion
- error production
- 最后一个策略 错误更正
- past 过去的错误处理
- 06-02: Abstract Syntax Trees (3m50s)【抽象语法树】
-
- 06-03: Recursive Descent Parsing (6m35s)【递归下降解析】
-
- example
- quiz
- 06-04: Recursive Descent Algorithm (13m28s)【递归下降算法】
-
- example
- Functions for non-terminal T
- summarize
- quiz
- 06-04-1: Recursive Descent Limitations (6m56s)【自顶向下递归局限性】
- 06-05: Left Recursion Part 1 (8m05s)【左递归】
-
- 左递归语法形式
- summarize
- CS-143 Week4 Bottom-Up Parsing 【自底向上解析】
-
- 07-01: Predictive Parsing Part 1 (7m40s)【预测解析】
-
- example
- 解析表进行解析的算法
- 07-02: First Sets (14m02s)【first集】
-
- first集合的计算
- example
- 07-03: Follow Sets (17m05s)
-
- algorithm sketch 算法概述
- example
- 07-04: LL1 Parsing Tables (14m41s)【LL1解析表】
-
- example
- 07-05: Bottom-Up Parsing Part 1 (7m06s)【自下而上的解析】
-
- example
- 07-06: Shift-Reduce Parsing Part 1 (5m40s)【移位规约解析】
- 08-01: Handles Part 1 (4m35s)【句柄】
- 08-02: Recognizing Handles (13m12s)【句柄识别】
-
- example
- 08-03: Recognizing Viable Prefixes (14m57s)【识别可行前缀】
-
- example
- 08-04: Valid Items (3m31s)【有效item】
- 08-05: SLR Parsing (14m16s)【SLR解析】
- 08-06: SLR Parsing Example (6m42s)【SLR解析案例】
- 0 8-07: SLR Improvements (11m49s)【SLR改进】
- 08-08: SLR Examples (12m47s)【SLR案例】
-
- example
Pre-Course Survey
一个小调查,无伤大雅
实验所需虚拟机
链接: https://pan.baidu.com/s/16KXICHhpBb22v4CyNQugMg 提取码: n44a
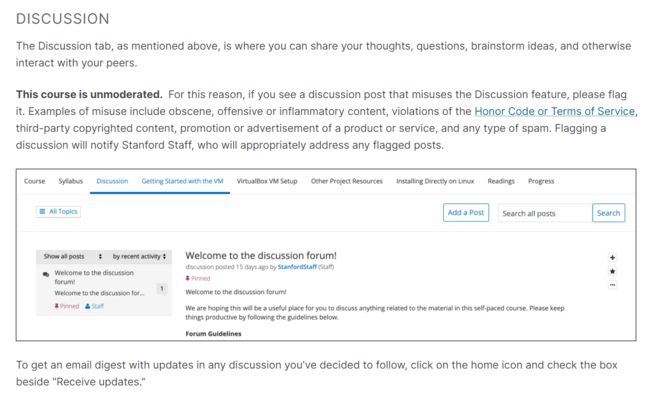
Navigation Your Course
课程导览
属性bar用的
介绍了 课程模块,大纲模块,讨论模块,测评模块,测评模块会打分
讨论模块要遵守规则,不发一些不必要的内容,淫秽色情,垃圾邮件,抄袭的内容
01-01: Introduction (8m20s)
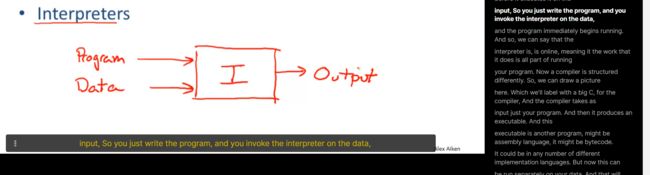
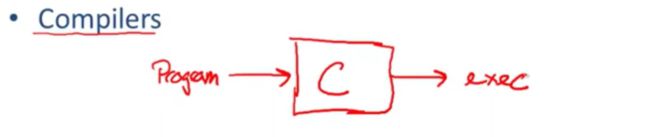
编程语言又两种实现,也就是编译器和解释器
解释器做了啥
我们将数据和程序发送给了解释器,解释器开始运行,有了输出,解释器相当于是一个在线的
写一个程序,产生了一个可执行文件,当然不只是可执行文件
可能是汇编,字节码之类的,
现在你不需要输入数据,就能得到输出
在结构中就是线下,
当然是相对于解释器的,解释器需要结合一个数据进行执行,而编译器不需要
因此,我们不需要对程序进行重编译或者做其他处理,我们就能对可执行程序传入很多不同的值或数据集进行处理
编译器开发历史:
IBM 704软件成本超过了硬件成本
用解释器比你直接跑代码会慢很多,10-20倍
fortran
直接翻译成机器可执行的,会快很多
formulas translated 公式翻译
有些仍然保留了FORTRAN 1的框架
什么是fortran 1 框架呢
lexical Analysis 词法分析
parsing 解析
这两个共同关注语言的语法部分syntactic
semantic analysis 语义分析,关注语义方面,包括类型和作用域
optimization 优化 运行的更快,更节省
code generation 也就是translation 转换,转换结果可以是字节码,机器码,或者是另一种高级语言
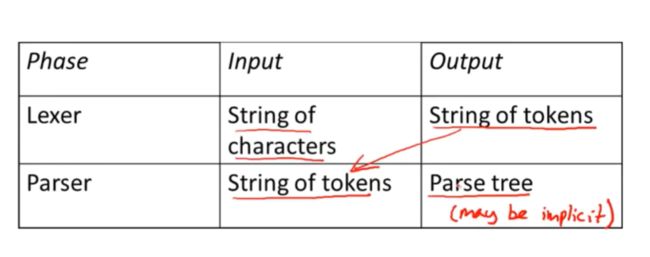
01-02: Structure of a Compiler (13m53s)【编译器结构】
first step:recognize words
对单词的认识/理解
this is a sentence
你需要理解 大小写,空格,句点才能够正确的理解这个意思
如果给我们一个其他的
ist his ase nte nce
is this a sentence
我们也无法很容易得到结果
词法分析的目标,就是将程序代码文本按照他的方式进行分词,
也就是对词的一个区分
这个句子,分为几个token呢(词法单元)
if,then,else,
x,y,z
1,2
=,空格 ,
同时,我们仍然要区分一个等于号和两个等于号
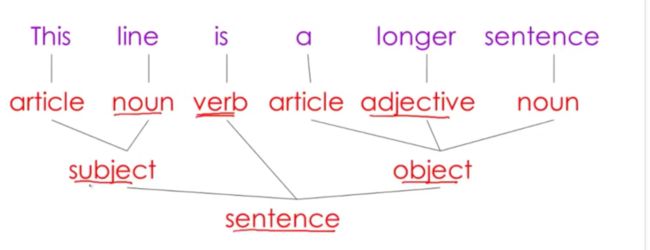
句法分析
分析词的意思后(名词,动词,形容词),我们就会有句法
(主语subject,谓语verb,宾语object)
共同构成了一个句子树,这就是一个英文句子进行语法分析的例子
代码也同理
针对if then else进行分析
if-then-else就是解析树的树根
如下为if-then-else的分析树
if then else
分成了三个部分,断言部分,then部分,else部分
if包含了 x == y
then包含了 z = 1
else 包含了 z = 2
句意分析
当理解句子结构厚,我们就要去理解这句话写了什么内容
编译器只能做有限的语义分析,找到自相矛盾的地方,
example
jack said jerry left his assignment at home
这里的his 我们无法知道他是指定jack还是jerry
worse
jaca said jack left his assignment at home
这个更糟糕的情况,我们不知道有几个人,jack是两个人,his是一个人?
可能性很多
编程语言中,为了避免这种尴尬,就有了变量绑定
非常严格的规则,防止歧义
如上的程序,会输出4
外层的定义jack会被隐藏
编译器执行文本的语义分析时,不需要考虑对变量进行作用域的绑定分析
jack和her的类型不匹配,肯定不是一个人
optiimization(优化)
比较像一个专业的编辑在一定的字数范围内对文章长度做删减
but a little bit like editing
替换为
but akin to editing
意思没变,但是词变少了,节省了资源
run faster,use less memory,lower power,database,network
一个需要优化的程序
y*0 和给x赋值为0 是一致的,因此我们比起乘法,仅仅做赋值即可
但是这个不是一个正确的规则
仅仅对integer有效
浮点数无效,
finally code Gen
也就是翻译成其他语言,编译器把高级语言转换为汇编语言
最基本的fortran对于语义分析会很小
而现代的编译器,优化会占据很大
01-03: The Economy of Programming Languages (19m51s)【编译器性价比】
本节课,将会谈论这三个问题,
为什么这么多的语言
为什么又新的语诞生
什么是一个好的编程语言
首先第一个
why are there so many progamming languages
首先我们是有三个大概的范围,应用领域不同
他们的优势不同,作用域不同,语言不同
科学研究:需要好的浮点数运算,FP,好的数组支持,大并行支持(parallelism)FORTRAN语言 (公式 翻译)fomulate translate
商业领域:需要好的稳定性,防止丢失数据,而且要可靠,需要报告的生成,数据分析,数据处理之类的, 也就是SQL比较常用
系统编程:也就是嵌入式,控制设备之类的,我们需要控制一些底层的资源,细粒度控制,需要能够预判时间(实时控制),在一定时间内做出反应,或者对网络进行大量的响应 广泛的就是c和c++
why are there new programming languages?
为什么需要设计一个新的语言
培养程序员以及培养某种语言程序员的成本 这个比较重要,如何教会他们去使用
因为去开发,去开发一个新的编译器的成本并不是很高
有如下的预测
有两点,也就是
第一个预测是 广泛使用的编程语言改变的很慢,会越来越保守
第二个预测是 很容易的去开发一个新的语言,培训成本为0,新的编程语言进化的会很快。
productivity > tranning cost
生产力要大于学习耗费
就会选择新的语言
什么时候呢?
需要一种语言去填补空白的时候(新的应用领域),往往 会选择新的语言
旧的语言不一定能够支持新的应用领域
新的语言有时候会看起来像旧的语言,就比如java很像c++
猜测:为了降低培训成本,通过学过的语言更轻松的去解除
what is a good programming language?
从语言设计的通用性来说,没有一个好的编程语言
讨论这个问题,无法达成共识,关于什么是好的语言,也没有普遍接受的共识,
讲师的猜测:
是大众的接受度/使用度,可以作为是一个好的语言的标准
Summarize
很难设计出一个整合你所有想要功能的语言
培养程序员花费了大量成本
02-01: Cool Overview (19m58s)【cool语言概述】
classroom object oriented language = cool
课堂专用面向对象语言
被设计短期内/一个学期内写出编译器,需要易于编写
本课程的目的:完整的编译器编写,包括MIPS 指令集
我们可以运行编译器,也可以生成mips汇编语言,然后可以在你能访问的任何机器上模拟mips汇编语言
分为五个任务,编译器本身包含四个阶段
词法分析
语法分析
语义分析
代码生成
我们编写如上模块采用的是 插件兼容
也就是,我们可以使用模板填充其他几个,然后我们只是去编写词法分析,然后和标准输出进行比对,保证自己编写的足迹按没问题
优化可以当一个可选的作业
开始编写程序
1- 每个cool程序必须要有一名为main的class
class main{
};
class 后面跟名字,然后花括号带分号结尾
一个程序包含若干类
main类中,main方法必须存在,这个方法用来启动程序,此外,这个方法必须无参,main方法永远无参
class Main{
main():Int{
1
};
};
在main类中,有一个main方法
cool中,需要对方法指明返回值的类型,这里写int
cool是一种表达式语言,也就是一段代码
表达式可以写的随意一点,即这个表达式对于这个方法的表达而言没有显示的返回语句
() -> a+b ,返回a+b的值
上面那个方法体中只有一个数字1 所以运行程序的时候,返回的就是这个方法的值
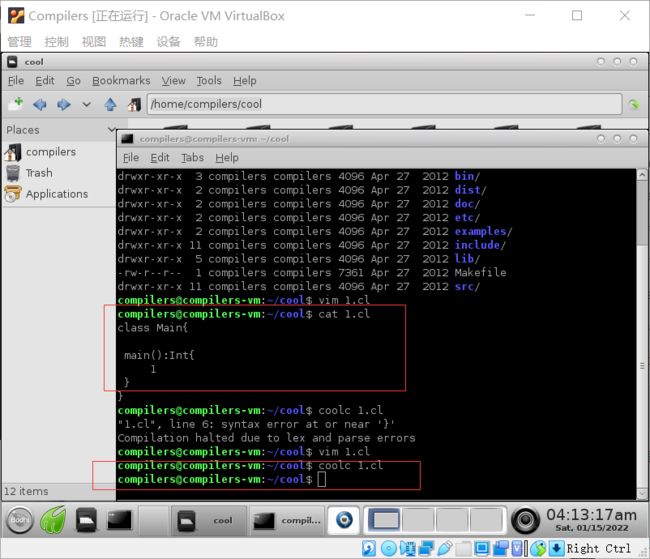
那么如何编译?
coolc就是cool的编译器,
coolc 1.cl
就会生成1.s的新文件,
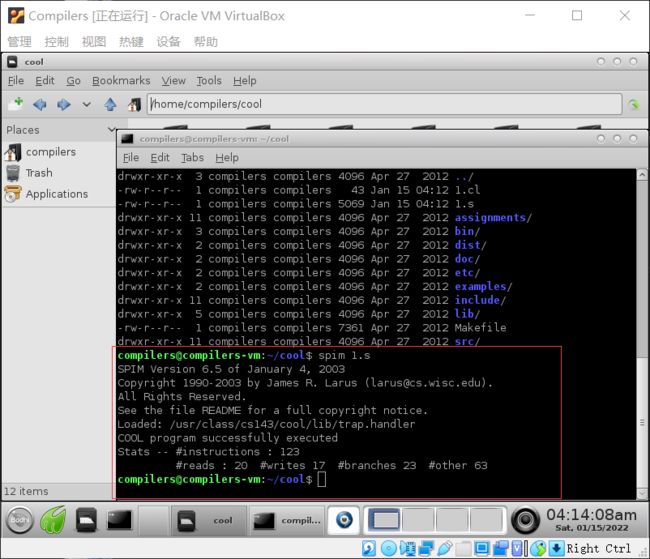
我们尝试运行,spim(mips模拟器)
接着出现了一些数据,例如 执行了多少条指令,load指令,store指令,和一些分支的数量
spim 1.s
stat里面的参数是为了让我们进行优化使用的,现在我们不需要考虑
如果在cool程序中打印出某些内容,则必须对此操作进行明确声明
cool中有特殊的类,也就是IO原始类
可以为main这个类进行属性的声明,我们声明一个属性为IO的i变量,同时给i分配一个新的对象,之后就能用它进行IO操作了
class Main{
i : IO <- new IO;
main():Int{
1
};
};
在main方法中,添加out_string的调用,
i.out_string() 就是我们调用方法的方式
我们尝试输出helloworld
class Main{
i : IO <- new IO;
main():Int{
{
i.out_string("Hello World\n");
1;
};
};
方法中语句块由用分号分隔的一系列表达式组成,
tips:
感叹号小贴士
!运算符跟着之前输入的命令前缀,就可以执行之前的命令
例如:
执行过coolc 1.cl
那么我们执行
!c
和coolc 1.cl是一样的
修改:
{i.out_string(“hello world”);}1; 很繁琐,修改成如下问题,但是返回值类型会不同,不是int了,类型匹配出错
class Main{
i : IO <- new IO;
main():Int{
i.out_string("Hello World\n");
};
};
因此我们修改成IO
class Main{
i : IO <- new IO;
main():IO{
i.out_string("Hello World\n")
};
};
当然我们可以增加自己的灵活性
main返回结果设置为object
class Main{
i : IO <- new IO;
main():Object{
i.out_string("Hello World\n");
};
};
这里我们在外面进行定义,我们可以直接在里面调用
class Main{
main():Object{
(new IO).out_string("Hello World\n");
};
};
或者说,我们main类直接继承io,main就能够拥有io的所有功能,cool中self等于this
class Main inherits IO{
main():Object{
self.out_string("Hello World\n");
};
};
或者,cool的特性,不显式命名调用对象的情况下调用方法默认为self
class Main inherits IO{
main():Object{
out_string("Hello World\n");
};
};
02-02: Cool Example II (15m04s)【cool样例2】
这次我们写阶乘,不写hello world
class Main{
main():Object{
(new IO).out_string("1\n")
};
};
我们想让用户输入,然后进行输出
需要调用in_string,同时为了美观,我们组合一个换行
class Main{
main():Object{
(new IO).out_string((new IO).in_string().concat("\n"))
};
};
我们输入多少,就会返回多少
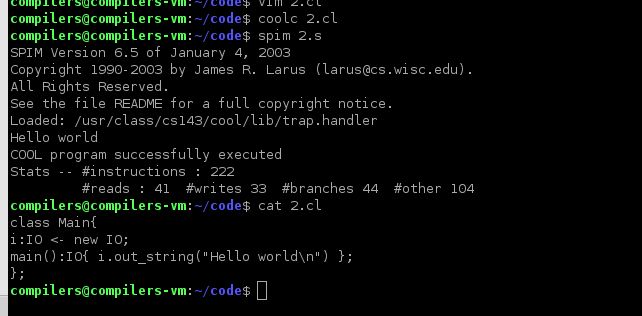
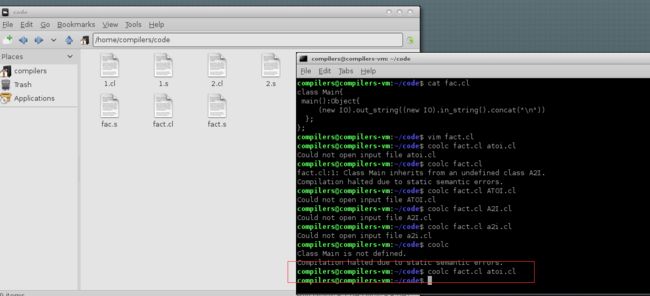
接下来,我们讨论如何将字符串转换为整数
阶乘计算需要对数字,我们这里接受的是字符串
cool中有一个专门编写的库用来做整数和字符串之间的转换
也就是A2I 意思是ascii码转换为整数
class Main inherits A2I{
main():Object{
(new IO).out_string(i2a(a2i((new IO).in_string())+1).concat("\n"))
};
};
代码的意思就是,输入的字符串ascii转整数 然后加一然后 整数转ascii(字符串)输出
但是编译器中没有提供a2i的相关函数,需要我们在编译的时候,指明我们需要的函数,
coolc fact.cl atoi.cl
我们找到相关atoi.cl库函数
复制到code中,即可编译完成
我们来编写阶乘,需要调用fact(阶乘)函数
在cool中,if的结构是 if-then-else-fi 也就是一个完整定义
这里可能会感到奇怪,i=0不是赋值么,但是这里确实是一个判断
class Main inherits A2I{
main():Object{
(new IO).out_string(i2a(fact(a2i((new IO).in_string())).concat("\n"))
};
fact(i:Int):Int{
if(i = 0) then 1 else i * fact(i-1) fi
};
};
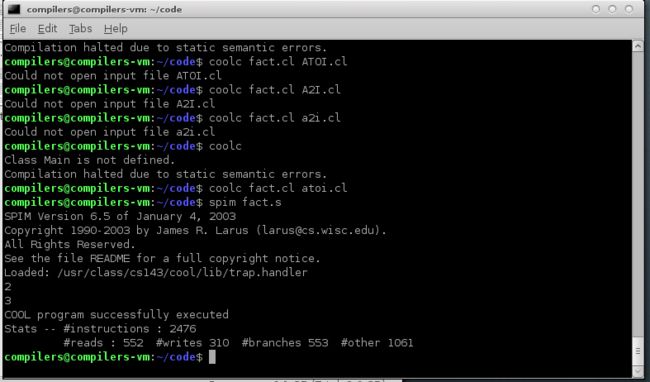
我们尝试把i == 0试试
发现编译失败
我们接下来使用循环来写阶乘
我们在cool中使用let声明局部变量
定义fact值为1
cool中赋值为<-
循环的开始和结束是loop和pool
最后一个语法块的值,就是这个方法的返回值
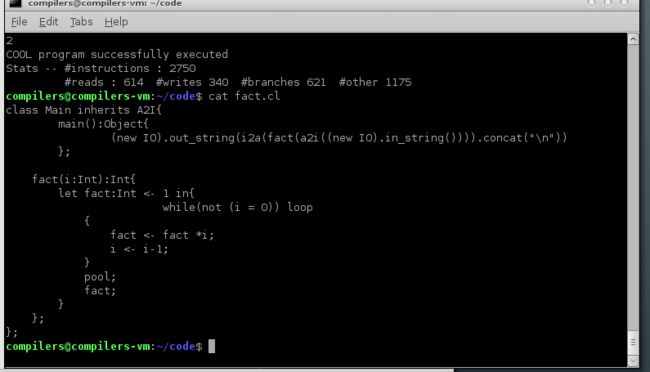
class Main inherits A2I{
main():Object{
(new IO).out_string(i2a(fact(a2i((new IO).in_string()))).concat("\n"))
};
fact(i:Int):Int{
let fact:Int <- 1 in{
while(not (i = 0)) loop
{
fact <- fact *i;
i <- i-1;
}
pool;
fact;
}
};
};
02-03: Cool Example III (18m05s)【cool样例3】
本次课程,我们学习创建list
let表达式可以定义多个常量,使用逗号做分隔符
class Main inherits IO{
main() : Object{
let hello : String <- "Hello",
world : String <- "World!!",
newline : String <- "\n"
in
out_string(hello.concat(world.concat(newline)))
};
};
没有问题
然后,我们不使用这样的引入,而是使用一个抽象的list,构建字符串列表
list都会包含两部分,一个是值,一个是next指针指向其他list
nil:List 如果不赋值,默认是为空的也就是void
isvoid cool自带的检查是否为空
class List{
item:String;
next:List;
init(i:String, n:List):List{
{
item<-i;
next<-n;
self;
}
};
flatten():String{
if(isvoid next) then
item
else
item.concat(next.flatten())
fi
};
};
class Main inherits IO{
main() : Object{
let hello : String <- "Hello",
world : String <- "World!!",
newline : String <- "\n",
nil:List,
list:List <- (new List).init(hello,(new List).init(world,(new List).init(newline,nil)))
in
out_string(list.flatten())
};
};
同样,成功输出
我们这里item可以进行修改,成为object
同时,我们需要修改flatten,通过case进行选择他的类型进行输出
如果传入int 那就i2a,其他同理
abort函数,终止并退出,返回一个object对象,但是这里的case需要返回stirng对象,我们放入语句块中
case分支必须分号结束
class List inherits A2I{
item:Object;
next:List;
init(i:Object, n:List):List{
{
item<-i;
next<-n;
self;
}
};
flatten():String{
let string:String <-
case item of
i:Int => i2a(i);
s:String =>s;
o:Object =>{abort();"";};
esac
in
if(isvoid next) then
string
else
string.concat(next.flatten())
fi
};
};
class Main inherits IO{
main() : Object{
let hello : String <- "Hello",
world : String <- "World!!",
i:Int <-42,
newline : String <- "\n",
nil:List,
list:List <- (new List).init(hello,
(new List).init(world,
(new List).init(i,(new List).init(newline,nil))))
in
out_string(list.flatten())
};
};
CS-143 Week2 Lexical Analysis&Finite Automata[词法分析和有限自动机]
03-01: Lexical Analysis (12m06s)【词法分析】
我们对该段进行分割
if(i == j)
z = 0;
else
z = 1;
将他们转换成为(token)词法单元,if,变量名 i,n,j 关系运算符,== 之类的
在词法分析器的眼中,是这样的
\tif(i==j)\n\t\tz=0;\n\telse\n\t\tz=1;
整个代码就像字符串,也可以类比作为字节
词法分析器通过绘制分割线,将字符串转换为词法单元
Token class(标记类)
光分词法单元是不行的,需要根据作用进行分类
这里类比在英语中,和在编程语言中的标记类
每个标记类,都会对应程序中的一组字符串,
比如:
名词:apple,banana,。。。
keywords:if,else,while
标记类对应一组字符串,也就是,这组字符串可以用来被标记类描述
identifier(标识符)
大多数编程语言中,标识符的标记类是字母或数字,以字母开头
例子:C语言中
integer(整数)
非空数字字符串
例:0,12,001,00,
keyword:
keywords:if,else,while
whitespace(空格)
空格也是一个标记类
例:if_ _ _()这里三个空格,就会被当作一个空格
词法分析的目标是根据程序的子串的角色,然后对其进行分类
这里的role就是一个标记类
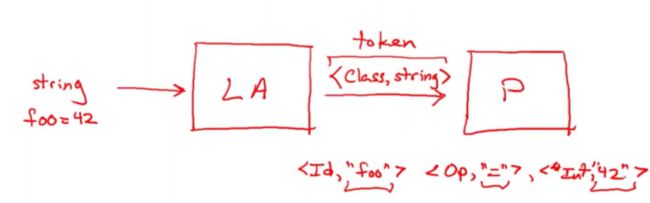
然后把标记类传递给解析器
这里是词法分析器和解析器之间的传递
1- 词法分析器获取到字符串,并存储为字节序列
2-发送给解析器的时候是一个序列对
例如:
如果字符串是
“foo = 42”
会传递三个token(词法单元)
传递的单元是以字符串形式来存储的,这里的42也是字符串
这些序列传递给解析器
词法分析器本质:
输入字符串并将其分块儿为成对的序列,其中每一个对都是一个标记类和原始输入的子字符串
样例分析
\tif(i==j)\n\t\tz=0;\n\telse\n\t\tz=1;
我们首先写一下标记类
whitespace 空格,回车,tab
keywords
identifiers
numbers(integer)
operator
特例: ( 、) 、;、= 这四个是单字符标记类,一组中只有这一个字符串
但是一个特殊的== 归类为关系运算符的标记类
这里使用开头首字母当作划分
\tif(i == j)\n\t\tz=0;\n\telse\n\t\tz=1;
w|k|(|i|w|o|w|i|)|w|w|w|i|=|n|;|w|w|k|w|w|w|i|=|n|;
Summarize
总结两点,
第一个:识别输入中与标记相对应的子字符串
tips 这是编译器的术语,这些子字符串称为词素lexemes(构成词的要素)
第二个,对于每个词素,我们需要确定标记类token class
token
Quiz
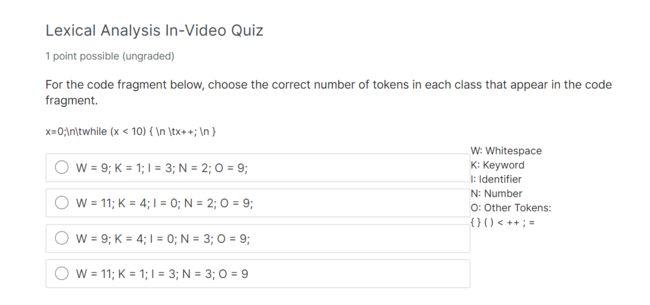
x=0;\n\twhile (x < 10) { \n \tx++; \n }
W: Whitespace
K: Keyword
I: Identifier
N: Number
O: Other Tokens:
{ } ( ) < ++ ; =
ionowwkwoiwownwowwwwioowwwo
虽然对空格有异议,但是I K N 是固定的,3 1 2
Note that '\t\n' is a single whitespace token. Also remember that 'x' is an identifier but 'while' is a keyword. Finally, note that '++' and '10' are both single tokens.
请注意“\t\n”是单个空白标记。还要记住,“x”是一个标识符,“while”是一个关键字。最后,请注意,'+'和'10'都是单个标记。
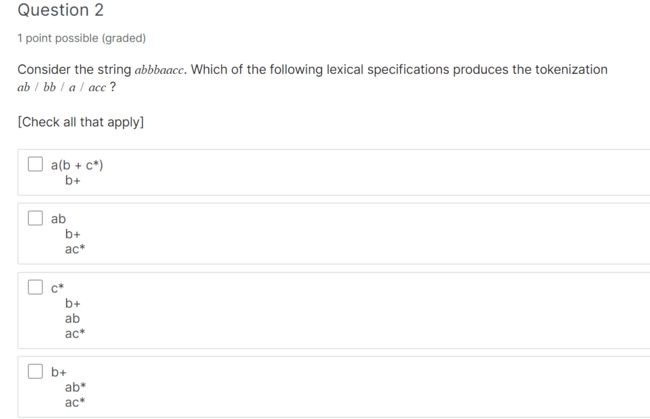
03-02: Lexical Analysis Examples (13m03s)【词法分析案例】
在fortran中,空格是不重要的
例如:VAR1 和 VA R1是一样的
fortran理念:你可以将程序中所有的空格删除,但是不会改变你程序想要表达的东西
tips:以后的例子部分来自龙书
这个例子是FORTRAN循环的头部
do 是循环的关键词,i的变换区间是在1-25
5是用来规定循环的范围
-do 5
|
|
|
|
|_
一共是延伸五个标签
根据标点的不同,第二行的作用也就不同,
第二行,do 5 I 5 I 5空格I其实是变量名 ,也就是说,第二行是赋值语句
DO 5I=1.25
我们怎么能够知道DO是干什么的?
从左到右逐个字符进行扫描,然后通过lookahead 向前看,许许多多的向前看
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-uAxJVCfb-1642520737888)(https://gitee.com/dingpengs/image/raw/master/imgwin/image-20220118153653605.png)]
在1之前,两者完全一致,当到了,.的时候,才会区分出来DO的作用
因此,词法分析系统的目标:最小化向前看,或者限定需要向前看的内容数量
为什么FORTRAN对空格不做检查?
因为对于打点编程,如果不忽略,容易造成误操作
翻译:这里的目标是为了将字符串分割,(也就是分割字符串,变为逻辑单元),从左到右扫描读取实现的,一次识别一个token
![]()
翻译:“回顾”也许就是决定一个词法单元的呢结束与下一个词法单元的开始
始终需要向前看(回顾)
为什么需要lookahead
假设我们读取到了else,这里存在lookahead问题,我读取e,是当作keyword,还是当作变量,还是某个大型语法单元的一部分呢?(因为变量i,z都存在对吧)
另一个是等于号,读取一个= 我们需要判断赋值过程中的等于号还是==
这些情况下,我们都需要lookahead
PL/1 keywords are not reserved
pl/1 programming language one(第一编程语言) IBM设计
这里是他的一个例子
example1
PL特性:不保留关键字,也就是可以使用关键字当作变量名
结构if-then-else,结构如下
IF Else THEN then = else;ELSE else = then
这造成词法分析很复杂
example2
DECLARE(ARG1…ARGN)
declare有n个参数,既可能表达keyword,也可能表达数组的引用
因此这个在词法分析器中的判断,需要lookahead,判断declare后面是否存在= 存在即为赋值,也就是作为了数组的名称
C++的bug
C++中,>> << 被当作输入输出流
如果在模板类中,Foo
这里就会存在bug,在词法分析器中会当作输入输出流
因此,如果模板类需要能够使用,这里需要加空格
也就是
Foo 这里的下划线是空格
Summarize
词法分析的目标是将输入流划分为词素
辨别每个词素的标记
正因为我们从左向右扫描,因此我们必须lookahead,回顾,才能够弄清楚当前正在查看的字符串,子字符串,的角色
03-03: Regular Languages Part 1 (11m48s)【正则语言part1】
简要回顾token/tokenclass
我们需要使用一种方法来指定每个字符串集所属的标记类,通常使用的是正则
regular expressions 正则表达式
每个正则就是一个集合
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-qDD9tt3C-1642520737899)(https://gitee.com/dingpengs/image/raw/master/imgwin/image-20220118225559463.png)]
基本表达式
对于单个字符,他的表达式所表示的集和就是这个单个字符
对于Epsilon(ε)代表的是一个单个字符的空字符串,不是空表达式,不代表空字符串
复合正则表达式
第一个,并集比较好理解,也就是
A+B 代表 A的集合和B的集合 合并
{1,2,3} {4,5,6} = {1,2,3,4,5,6}
第二个,级联AB 相当于所有来自A表达式所示集合的小a,与来自B表达式所示集合小b进行级联
也就是 一个叉积的操作
{a,b}与{c,d}级联得到{ac,ad,bc,bd}
第三个
A* A STAR
A的i次方表示他自己和自己级联i次,这里也就是A^i
当i等于0的时候,也就是A^0 这个时候也就代表ε(Epsilon) 这个表达式包含空字符串
也就是空字符串永远是A*的一个元素
匹配字母表的正则表达式Σ是最小表达式的集合
也就是说,我们先定义一个集合R,它包含哪些呢?
R = ε 因为ε永远是他的一个元素,代表了一个空字符串
或者他是单字符串c,c表示字母表中的一个元素
R+R代表的是一个正则和一个正则的集合/并集
RR代表的是正则的级联
R*则代表正则表达式的迭代
这五个例子是基于给定字母表的正则表达式集,也即是R的所有情况
如上 也就是正则的语法
example
我们需要知道组成正则的字母有哪些,这里简化使用了0,1
Σ={0,1}
1* 的正则表达式 *代表着从1到i的并集,i大于等于0
也就是""(空字符串)+1+11+111+1111+11111+111(i个1)111 这就是1*的所有字符串
第二个例子(1+0)1 也就是{ab|a∈1+0 且 b∈ 1}
最终结果就是{11,01}
第三个例子 0*+1*
0*代表的只有0字符串
第四个例子(0+1)* 也就是""(空字符串)+(0+1)+(0+1)(0+1)+(0+1)(0+1)(0+1)+(0+1)(0+1)(i个(0+1))(0+1)
(i个(0+1)) 代表的是 有i长度的字符串,每个位置都能用0/1来替代
第四个例子整体的意思就是,我们整个字符串 由0和1 组成不论长度
当你有一个正则表达式可以从字母表(也就是所给的集合) 中形成的所有字符串的集合时候,就会有一个特殊的名称Σ*
也就意味着所有字母字符串都可以根据需要进行多次级联
同时,不同的表达式能够表达完全相同的集合
比如第二个例子,11+10 === (1+0)1
或者 1* 和 1*+1
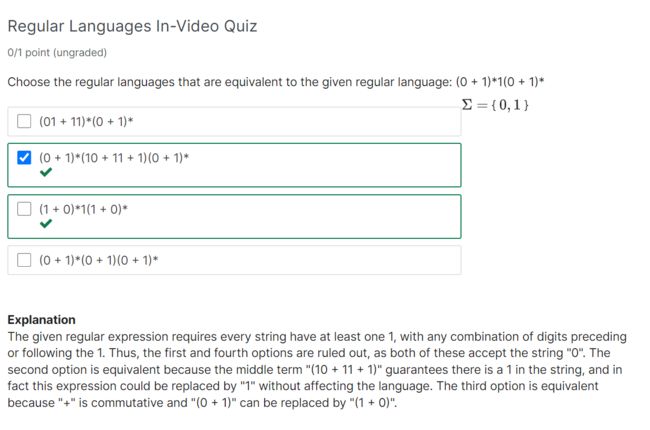
Quiz
需要选择结果相同的
(0+1)* 1(0+1)*
这个的意思就是 由0和1组成的任意字符串
第二部分的意思就是 (0+1)* 每一个字符配一个1组成一个集合
也就是 任意字符串+1+任意字符串
我们在选项中,挑选一个合适的
这里因为是多选,答错了(焯)
给定的正则表达式要求每个字符串至少有一个1,且在1之前或之后有任意数字组合。因此,排除了第一个和第四个选项,因为这两个选项都接受字符串“0”。第二个选项是等效的,因为中间词“(10+11+1)”保证字符串中有一个1,实际上这个表达式可以替换为“1”,而不影响语言。第三个选项是等效的,因为“+”是可交换的,“(0+1)”可以替换为“(1+0)”。
Summarize
我们学了正则表达式的语法,(正则语言)
标准定义中有五种正则表达式,
一个空字符串表达式ε,一个只包含一个字符的所有字符串表达式
三个复合表达式,并集,级联,迭代,
03-04: Formal Languages (13m40s)【形式语言】
在编译器内部,通常会操作多种不同的formal languages,正则表达式就是形式语言中的一个例子
形式语言的定义:
一个形式语言要有一个字符集(就如同ascii字符集),使用Σ来指代这个字符集
那么Σ对于这个formal language 指代的就是一组字符串
总的来说 一个形式语言就是基于一些字符所构建的任意字符集
在这个例子中(正则语言),我们由几种方式来创建字符集
例子:Σ ={1,2}
一个比较熟悉的例子就是英文字母表,可构成单词,可构成句子
但是不能叫做严谨的formal language,有些构成的句子不是句子
严谨的formallanguage是:
ASCII作为c编译器的所接受的输入集
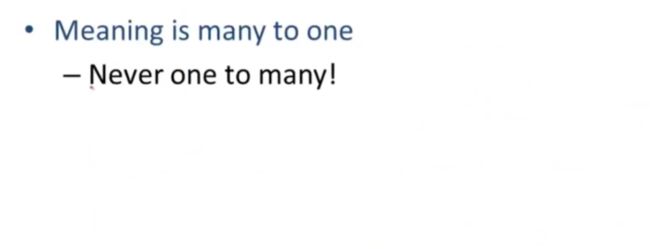
另一个重要的概念是meaning function
例如:f(x) = a(x)+b(x) 在编译器编译的时候直接替换为a(x)+b(x)
L(e)是正则表达式,M是对应的字符集
这是由正则表达式所表示的正则语言,
然后我们取上节课的例子
左边是表达式,右边是集合
A是表达式 a是集合 a属于A,即a复合A这个表达式的规则
meaning function就是为了解决这些问题,使得定义明确
关于正则表达式含义的正确定义,我们使用L(…) 来进行显式表达
通过L(…) 递归的将符合表达式分解为多个子表达式
也就是对子集 计算得到最终的集合
为什么使用meaning function
1- 确保语法清晰,语义清晰,(表达式AB,集合ab)
2-允许我们考虑 语法和语义分开,改变语法,语义不变
3- 语法和语义不是一对一的 多个表达式一个意思
语法和语义分开的好处
罗马数字和阿拉伯数字,同样的意思,但是写起来,做起来的语法完全不同,难度也不同
符号非常重要,能够决定你的思维方式,这也是分离语法和语义的重要原因
多个表达式表达一个语义
0* 0+0* 等等,这些都表达一个意思
左侧代表不同的表达式,右侧代表语义
这就是formal languages 的一个通用特征,
对编译器非常重要,这就是优化的基础
含义是多对一的关系, 绝不是一对多
03-05: Lexical Specifications (16m19s)【词法规则】
keyword
我们首先来写一个if的正则表达式
也就首先是i的和f的,然后串联在一起,然后与else做一个并联
'i''f' + 'e''l''s''e'
很显然,这个else比较复杂,我们选用c系列,(单个字符的系列也可以)
'if'+'else'+'then'+'...'
integer
一个非空的数字字符串
如下也就是单个数字的对应字符串集合的正则表达式
'0'+'1'+'2'+'3'+'4'+'5'+'6'+'7'+'8'+'9'
因为比较常用,因此我们可以定义为一个常量
digit = '0'+'1'+'2'+'3'+'4'+'5'+'6'+'7'+'8'+'9'
这个digit正则表达式 可以表示集合中的任意一个数字
多个数字如何匹配?我们可以做一个简单的迭代,并将空字符串去掉
digit digit*
这样的迭代就保证了,开头必须一个数字,后面紧跟0或者更多其他的数字
例如:至少要一个A 就可以写成AA* 每个正则都会支持,A^+ === AA*
identifier
由字母和数字组成的字符串,以字母开头
我们直接定义一个所有字母的letter
letter = 'a'+'b'+'c'+'d'+'e'+'...'
同时我们可以简写为:(通过使用character range的正则表达式)
letter = [a-zA-Z]
最终的结果就是letter(letter+digit)*
whitespace
需要识别tab 空白,换行 rubout(退格)等非空序列,因为是要非空的,因此我们直接加puls
(' '+'\n'+'\t')^+
课外example
邮件的匹配
letter^+'@'letter^+'.'letter^+'.'letter^+
ALGOL语言家族中的Pascal语言,和fortran 和c是同一个家族
他的num 数字由 digits opt_fraction(分数) opt_exponent(表示指数) 组成
digit 通用数字的并集
digits是digit^+ 非空数字集合
如何定义的的分数和指数呢?
分数实际上就是 小数,
opt_fraction = ('.'digits)
第一个部分表示小数点后跟着一连串数字,ε 表示这个数字的分数部分可以存在或者完全不存在,也就表示了这部分是可选的
也就是可选分数
可选指数 也同样是因为和ε做了并集,这样的话,整个指数部分就是可选的
3298e+10
('E'('+'+'-'+ε)digits)
指数永远E开头 ,digits一个非空数字字符串
他俩中间包含了可选的,中间可有可无,这个符号可以是- 也可以是+
+ 是或的关系
通常写法:
把加ε 当作可选的,通常写作('.'digits)?
指数可以写作('E'('+'+'-')?digits)?
Summarize
使用正则来描述许多有用的语言(描述email,phone number等)
正则语言作为一种语言规范,仍然需要一个词法分析的实现
下次课:判断给定字符串s和一个正则表达式R,如何判断字符串是否在这个正则表达式所定义的集合呢?
04-01: Lexical Specification (14m30s)【词法规则2】
快速总结
有一个重要的:[a-z]的补集为[^a-z]
表示除了a-z的所有字符
给定的字符串s就是正则表达式所代表的集合中的元素
L® 他的语义其实就是一系列字符串,s属于L®
但是,仅仅能够将字符串归为某一个正则下,回答yes/no,是不够的,我们需要针对正则表达式进行小拓展
1.Write a rexp for the lexemes of each token class
当我们想要设计一门语言的词法规则的时候,我们需要为词法写出正则表达式
这样才能构成token类
上图是上节课我们所定义的
2.Construct R,matching all lexemes for all tokens
第二步,我们要做的就是去构建一个能够匹配所有词法单元的负责的正则表达式
也就是做所有正则表达式的并集
3.Let input be x1…xn
假设我们输入的是x1…xn
然后把每个前缀去检查,是否满足正则表达式的函数
也就是说,输入abcd
检查的是
a
ab
abc
abcd
所以叫检查前缀
![]()
4.if success ,then we know that
如果匹配成功,我们就能能知道,他这个x1x2x3 是我们token中的一个
5.remove x1…xi from input and go to (3)
然后我们将前缀进行删除,也就是我们把我们匹配到的删除,然后跳转到第三步,接着去检查前缀
也就能持续的去检查,直到为空字符串
question
how much input is used?
输入值中的内容有多少确实被用上了?
![]()
也就是说,我们的开始相同,但是我们的结束不同,那么,token会取哪个?
example:双等号(==)
一个等号赋值,两个等号比较运算符
我们需要的方法是:最长匹配(maximal munch)
两种都有效,我们选择更长的token
which token is uesd?
匹配到多个词法单元,我们选择哪个?
也就是说,一个keyword的正则包含if,一个标识符的正则也包含if,
在大部分语言中,标识符实际上不包含关键字
因此这里需要采用优先度顺序来进行选择,这个规则优先选用列表在前面的
优先选出列出的第一个标记类,也就和词法规则中,我们将关键字的匹配放在标识符之前
what if no rule mathes?
我输入的前缀不符合词法规范的表达式语言,怎么办?
当然是做好错误处理,提供程序员错误的位置和错误类型的反馈
当然对于词法分析来说,最佳的解决方案是 编写意类错误字符串的正则
也就是不在语言词法规则中的当做另一个种规则,
同时,把该规则放在最后面
Summarize
翻译:
正则表达式可以匹配各种字符串类型
在词法分析种使用需要一些拓展
消除一些特定的歧义,匹配最长的字符串,最高优先匹配度
错误的处理,写一个可能错误字符串的正则,赋予最低的优先级
优秀的一些算法(之后的课程)
可以只进行一次遍历
对于每个字符进行很少的操作,仅仅需要一个简单的表的查找
04-02: Finite Automata Part 1 (13m01s)【有限自动机】
正则实现模型
通过有限自动机,来方便大家了解他内部使用正则表达式的实现机制
正则表达式和有限自动机关系密切,都是同一种语言,也就是正则语言
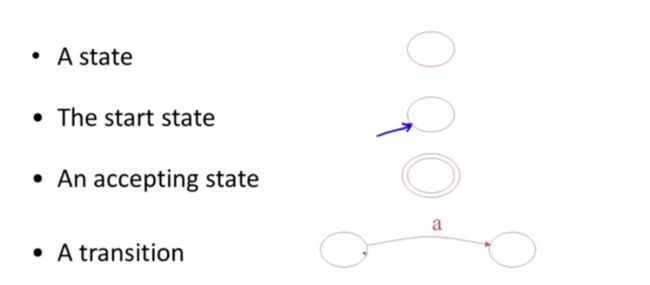
有限自动机的标准定义:
1- 包含了一组能读取的输入字符集
2-他管理了一系列状态
3-特殊的一个开始状态
4- 一组用于接收状态的集合
(自动机在读取这些它可以接受的状态输入后回自动结束,否则拒绝这些输入,因为他们不符合规则)
5- 自动机有一些用于状态转化的集合(输入转换到另一种状态)
Transition
关于有限自动机的转换细节
处于状态(s1) 读取到输入值a,自动机就能将他转换到状态2(s2)
如果输入结束,那么自动机就会以此结尾的输入所转换得到的状态作为接受状态(例如:z=1+a,自动机初始状态为1.接收的输入值是z,我们输入123123,最终的接收状态为224124)
如果不满足上面的条件,就会拒绝输入(就好比 写代码过程中,IDE根据输入自动提示错误)
例如:
因为状态s而终止,也就是 状态s不属于最终状态集,或者是 接受状态集
除了以接受的状态结束以外,其他任何状态都将被拒绝
或者
如果当机器卡住的时候,意味着他自己处于以重无论输入什么都不会发生转换的状态
也就是有一个news的状态集 输入了A但是美有规则可以将A转换到对应的指定状态,这样他就卡住了,也算一个拒绝状态
上面的例子也即是 到达输入的末尾,但是自动机并未处于最终状态或者说,由于卡住永远不会到达末尾,都会拒绝输入
也就是,
该字符串不是有限自动机的语言(也可以理解为 没有正则处理的字符串)
另一种有限自动机的表达方式
一个圈表示一个状态,
一个箭头一个圈代表开始状态
两个圈代表接收状态
一个单项箭头链接两个圆表示状态的转换
编写 只接受数字1的自动机
例子1
一个开始状态,接受到数字1 然后转变为了可接受状态
在状态A侠,我们输入字符1,我们同时用指针来直向当前输入值的位置
指针输入就会前进,不会回退,输入字符的时候,指针向右移动
在状态b的时候,我们的指针到了1的后面,位于输入的末尾
我们处于接受状态,再传入一个输入结束的信号,我们得到最终的accept
下一个例子:
当我们在状态A的时候,我们开始输入,我们的指针读取发现0并不会发生转换,所以是reject
另一个例子
我们在状态A的时候,输入10 指针开始读取,然后读取到1 状态发生转换,可接受状态,也就是B的最终状态,接受状态,但是输入流仍然没有完,B的状态不能处理0这个输入,同样reject这个字符串
tips:
自我感悟:不知道对错:轻点喷
这个有限自动机,感觉学到这里,他应该是用来处理ifelse,A状态输入了if,正常语句后面会有其他的,但是B的状态转换为可接受,但是,B拒绝输入后续的字符,直到读取到了else,B接着向后转换
通常,我们上所说的有限自动机语言,他等价于接受的字符串的集合(也就是正则表达式所指代的字符串的集合)
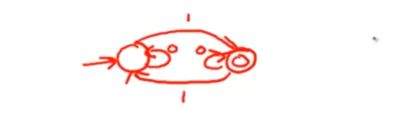
complex的例子
尝试写一个自动机,该自动机接收任意数量的1并后跟一个0
也就是,当读取到1的时候,自循环,当读取到0的时候,状态改变
例如我们在状态A的情况下,我们输入110
例如我们输入一个拒绝的例子
![]()
当我们读取到这里,虽然我们B是接受状态,但是仍然会reject
另一种转换,输入指针会一个一个移动
一种空跳,也就是说我们不需要输入东西就能够自动的跳转到另一个状态
空跳的时候,指针不会发生改变
空跳是一种无消耗的移动
自动机并不是必须要空跳,是可以选择的
Quiz
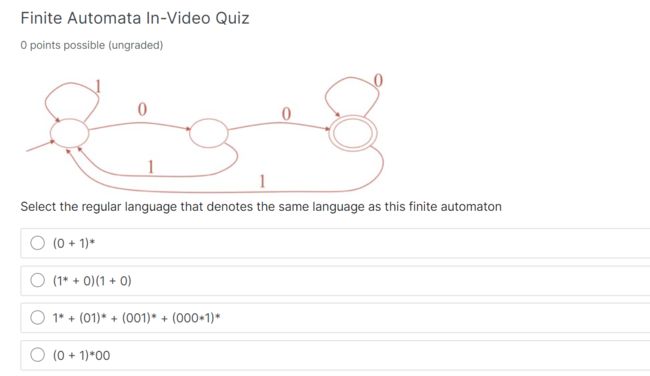
Select the regular language that denotes(标志) the same language as this finite automaton
选择表示与此有限自动机相同语言的常规语言
因为 1 在循环,所以首先肯定是我们接受到1,同时101 1001 也是循环
需要末尾是0的 1不限制,
(0+1)* 代表着 01 不限制
(1*+0)(1+0) 任意数量1 补一个0 然后 ×(1+0)补一个1,或补一个0,
1*+(01)*+(001)*+(000*1)* 这个也就是 全1
(0+1)*00 任意01补00
很明显,就是D
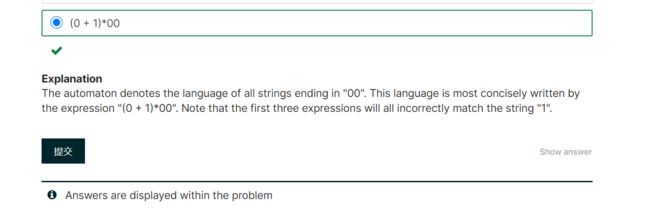
Explanation
The automaton denotes the language of all strings ending in "00". This language is most concisely written by the expression "(0 + 1)*00". Note that the first three expressions will all incorrectly match the string "1".
解释
自动机表示以“00”结尾的所有字符串的语言。这种语言最简洁的表达方式是“(0+1)*00”。请注意,前三个表达式都与字符串“1”不匹配。
DFA 和NFA
通过两个属性来确定有限自动机
没有空跳,也就是必须要消费输入值
对于确定性自动机 每个输入和每个状态之间只有一个转换(也就是,自动机的任何一个状态都不会出现同一种输入匹配了两种可能的状态)
对于非确定性自动机
这些是不起欸的那个的,尤其是非确定自动机可以仅需空跳
一个输入也可以进行多个转换
确定性自动机和非确定性自动机的区别就是 有没有空跳
确定性自动机的关键特性 是每个输入只能通过状态图的一条路径
不确定自动机却不是可以进行状态转换
对于何时接收不确定自动机的规则是:如果有任何路径可以被接受,则接收(也就是能够接受多条路,就接受)
输入会导出多个状态
在运行过程中,根据NFA不同的选择,他们能进入不同的状态
也就是if...else if ...else
这是一个小的自动机
当输入0的时候就会有两种状态
当我们输入1的时候,循环,
当输入0的时候,既可以是状态A,也可以是状态B,都是可能的
当我们又读一个0,我们既可以到C,也可以仍然是A
每一个步骤不确定自动机都有自己的一组状态,并且在需要的时候,我们考虑输入的所有可能动作,并计算出自动机下一步可能出现的完整状态集
当然,我们在输入最后一个0之后,必须要决定机器最终接受的状态
如果在这个集合中有任何最终状态,那么自动机都会接受他
就比如这个例子,我们读取到最后一个0,接受状态C,自动机就会接受
NFA和DFA以及正则表达式都有相同的能力,他们都是指定的正则语言
DFA比NFA快很多,不需要考虑其他可能
但是NFA的优势是比较小,会小很多
NFA 小巧紧凑,DFA执行速度快
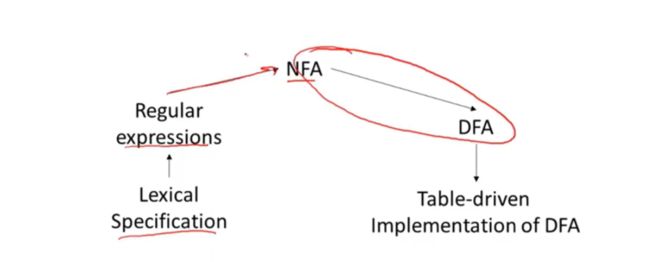
04-03: Regular Expressions into NFAs (9m41s)【从正则表达式到NFA】
我们需要实现一个词法规范
也就首先需要一个正则表达式,一个词法规则,做词法分析
需要将正则表达式转换为非确定性有限自动机
一部分非确定性自动机会转换为确定性自动机
最后我们使用一组lookup tables(查找表) 通过代码对这个表进行遍历,
以此来实现确定性自动机
for each kind of rexp ,define an NFA
我们要实现的就是每种正则表达式对应的非确定性自动机
我们使用L表示开始状态,使用两个圆来表示最终状态
我们只需要处理开始状态和最终状态,不需要担心自动机的整体结构
我们设计的自动机只有一种最终状态
对于epsilon
对于单个字符,我们也是直接的进行装换
![]()
复杂的正则表示
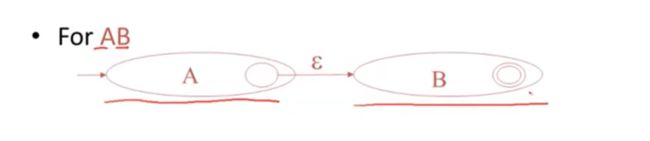
对于AB 级联
AB两个自动机合并,虽然A的状态转变了,但是并不是整体自动机的最终状态
也就是我们不会损耗(消费)任何输入,就能够提走到自动机B
对于A+B union
意思是无论找个输入是属于自动机A所接受的语言,还是自动机B所接受的,我们整体的都能够接受
找个地方就是一个不定项,都可以走,然后才会具体的读取字符串,看选则哪个
同时使用空跳,跳转到最终状态
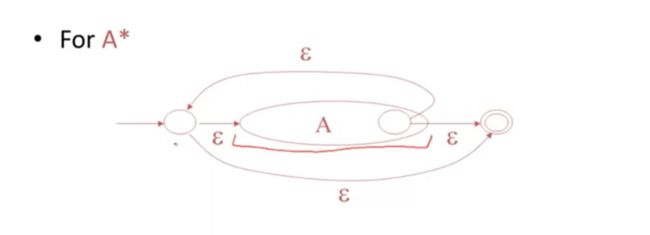
对于A的迭代A*
Epilon始终属于A*
从开始状态,接受空字符串,直接转到最终状态
在A的最终状态,我们通过空跳,直接跳转到开始状态
在A中循环迭代
也就实现了,能够识别0个或多个A中所接受的字符串
example
1+0)*1·
我们首先看看这个正则表达式的结构,然后用来画自动机
简单的构成复杂
首先自动机接收1,一个自动机接收0,组合起来,两个都接受,空跳,然后空跳到自己的最终状态
我们把小自动机放在 迭代的自动机模式里面
另一个是接收1的自动机
然后我们将她两个进行级联,直接空跳,标记好最终状态
quiz
Choose the NFA that accepts the following regular expression: 1* + 0.
1*+0 也就是不限量个1后面跟一个0
我们的A* 长这样,我们的1* 也要长这样
先排除AD,没有返回的空跳,
答案就是B了
由小到大,A+B是两条路径
Try to build the NFA from machines that you already know. Start with the machines for "0" and "1", then build the machine for "1*" and finally for the union of "1*" and "0".
尝试从你已经知道的机器上构建NFA。从“0”和“1”的机器开始,然后为“1*”构建机器,最后为“1*”和“0”的并集构建机器。
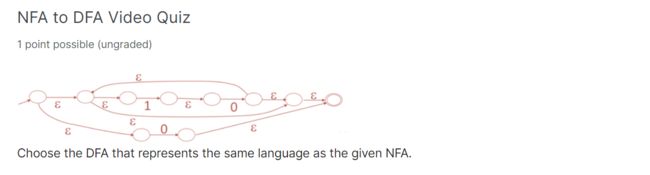
04-04: NFA to DFA (15m12s)【从nfa到dfa】
本次课是NFA到DFA
举例
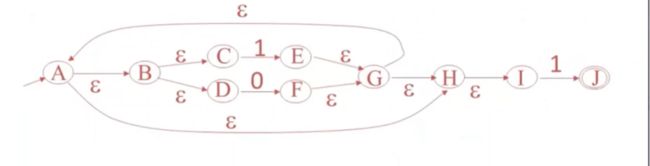
上节课的NFA
我们来选出epsilon-closure(这里我觉得是某个点的状态),这个我感觉像可达的集合
epsilon-closure(B) = {B,C,D}
epsilon-closure(G) = {A、B、C、D、G、H、I、}
nfa一个输入有多个不同的状态,
如果解决有多少个不同的状态,我们也就能够使用DFA来确定
对于epsilon-closure(B) = {B,C,D} 用到的状态数量肯定是小于等于n
那么将这个数量使用一个子集表示
他的子集有2^n-1个子集
这样我们就可以转换DFA,找到一个能够用确定性自动机模拟非确定性自动机行为模式的方法,
任意的非确定性自动优先级映射到一个等效的确定性有限自动机
NFA中,所有的状态S集合
初始状态、结束状态,s和f当然都属于S
我们尝试写一个状态转化函数,用它来定义运算符,这样在定义DFA时会很方便
a(x) ={y|x∈X ∩ x-a-> y}
epsilon-clos
DFA需要有哪些东西呢?
除了空集意外,这些状态都是状态S的子集
因此,这些DFA的状态,都会是NFA的状态的所有可能子集
DFA的一种状态就对应了NFA的状态的每种可能子集
DFA的开始状态是什么呢 非确定性自动机关于开始状态的epsilon-closure即epsilon-clos(s)
DFA的每个状态,都对应了一个不同的状态子集
DFA的每个状态,会告诉我们他们所可能在的NFA的某个特定状态集中
当然,NFA的开始就是epsilon-clos
(DFA的状态,都是NFA中的状态集)
最终状态包含了,{x|x∩F≠空}
集合x与nfa的最终状态集相交,并且他不为空集
DFA的一个最终状态,都有至少一个NFA的最终状态在这个集合里面
接下来我们定义一个转换函数
我们给定一个状态X,状态Y
有一个用于转换的a
在NFA中,我们想要知道输入a所达到的状态,也就是a(x)
有字符a输入,就能从状态x中获得结果,也就是字符a符合x集合中的哪一个执行路线
但是在这个后,仍然有空跳的可能
因此,我们加一层clos
x和y的转换
Y = epsilon-clos(a(x))
对于任何的X,都只有这样一个状态集,
(即一个输入字符只能对应一条执行路线,这个路线包含了一系列的多个状态)
也就保证了确定性自动机
有开始状态,最终状态集,,而且针对输入只存在一种移动路线的转换,并且没有空跳
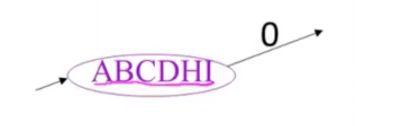
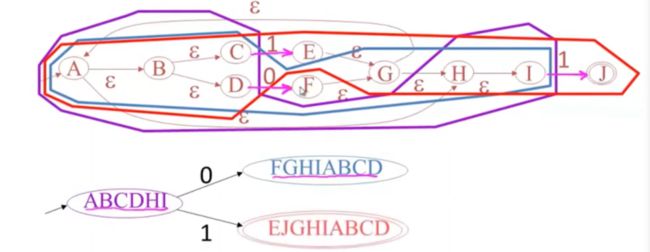
example
使用非确定新自动机来构筑确定性自动机的例子
这个非确定自动机的初始就是epsilon-clos
也就是这个紫色的,
所以DFA的开始状态就是状态ABCDHI的子集
从开始状态后,我们算出每个输入会让自动机发生的变化,也就是1和0
0的话也就是有D到F
因此,放到公式中,第二个状态对应了一个更大的集合epsilon(F)
当输入1的时候,可能从C-》e 也可能I -》j,当然还可以进行空跳
所以,除了F,他都可达,而且她包含了最终状态
当然,我们做一些补充,一些跳转
这个就是完善的确定性自动机
每一步转换都记录了NFA的集合
Quiz
选择代表与给定NFA相同语言的DFA。
首先起始状态,也就是直接包含空跳的
然后我们可以分支,一个1一个0
如果是1,我们寻找带1的,同时空跳的
带0的
除了中间两个,全都是
说明,0跳转后,通过1可以转换,1状态也可以通过0互相转换
看图说话,起始状态 通过0也可以自己循环
首先排除B,因为我们这个是两条路,
一条直接通过0 到达 了最终状态
另一条通过则为
因为如果从0直达最终态,不能返回1,所以,他的另一条路独立
排除B
04-05: Implementing Finite Automata (11m56s)【实现有限自动机】
实现有限自动机的时候,有时候可以不通过转换DFA直接实现
A DFA can be implemented by a 2D table T
从DFA开始,可以很简单的通过二维的形式来实现一个确定性有限自动机
一个维度是states状态
一个维度是输入符号
![]()
一个状态i和一个输入a 能够确定所要移动的下一个位置k
这张表,保存每个特定的输入和状态,以及自动机会达到的下一个状态
example
二维 表 2 dimension
DFA转换程由表驱动实现的例子
![]()
三个状态,两个输入
看图说话,填好我们的表格
然后通过打表 写出代码
i = 0;
state = 0;
while(input[i]){
state = A[state,input[i++]];
}
最开始状态,i和state都是0
然后我们需要对输入进行遍历,并对他进行检查,判断它是否需要跳转
我们输入一个字符数组input[i],数组元素不为空的时候进行跳转
我们上面的表我们定义为A,他是一个转换关系表
state = A[] 在A中寻找
通过一个当前状态和输入进行寻找
也就是A[state,input[i++]];
一个用于input数组遍历,一个用于对遍历得到的每个字符进行转换
一维表 1dimension
这个方法对于表的重复比较高,我们可以通过略微不同的表达方式来节省空间
使用一张一维表 也就是链表,共享表
因为词法分析中,重复的行非常常见
在dfa中可能会有2^n-1个状态(子集) 对于NFA则有n个
NFA直接转换自动机
因为NFA 转DFA 再转表,会造成很大消耗
直接NFA打表,
但是这个里面填入的都是集合
这样的话,他相当于是在递归,内耗比较大,因为他每一个都是一组状态
当然这样节省了表空间,执行速度会慢很多
summarize
实现词法规则的关键思想就是将非确定性优先自动挡及转换为确定性有限自动机
(也就是,把不确定的,赋予了确定的特性)
工具需要在速度和空间上权衡
DFA faster,less compact
NFA slower concise
week2 Quiz
答案31
We have 16 distinct strings of length 4, 8 distinct strings of length 3, 4 distinct strings of length 2, 2 distinct strings of length 1, and one empty string. In total, we have 16+8+4+2+1=31 distinct strings.
我们有16个长度为4的不同字符串,8个长度为3的不同字符串,4个长度为2的不同字符串,2个长度为1的不同字符串,以及一个空字符串。我们总共有16+8+4+2+1=31个不同的字符串。
2*2*2*2+2*2*2+2*2+2+1
那个词法规则可以分割成如下这样
emm,这个我看不懂他选项,他写的不是一个完整的式子,先跳过
Both rule 3 and 4 match the whole string, while 3 has a higher priority.
规则3和4都匹配整个字符串,而规则3的优先级更高。
In this NFA, there are five states, S0, S1, S2, S3 and S4. S0 is the start state, S4 is the accepting state. The transactions are following.
If we are in state S0 and read input 0, we go to S1.
If we are in state S1, we can go to state S3 without consuming any input, that is a -move. If we are in state S1 and read 0, we go to S2.
If we are in state S2 and read 0, we go to S0.
If we are in state S3 and read 1, we go to S4.
If we are in S4 and read 0, we go to S3.
在这个NFA中,有五个状态:S0、S1、S2、S3和S4。S0为开始状态,S4为接受状态。交易如下。
如果我们处于状态S0并读取输入0,我们将进入S1。
如果我们处于状态S1,我们可以在不消耗任何输入的情况下进入状态S3,这就是移动。如果我们处于状态S1并读取0,则转到S2。
如果我们处于S2状态并读取0,则转到S0。
如果我们处于S3状态并读取1,则进入S4。
如果我们在S4,读0,我们进入S3。
CD只是包含了ab,而不是正则的(abab)*
We need 4 states, S1, S2, S3 and S4. S1 is start state and S4 is the accepting state.
If we are in S1 and read input a, we go to S2.
If we are in S2 and read input b, we go to S3. If we are in S2 and read d, we go to S4.
If we are in S3 and read c, we go to S2.
我们需要4个状态,S1,S2,S3和S4。S1为开始状态,S4为接受状态。
如果我们在S1中,读取输入a,我们进入S2。
如果我们在S2中,读取输入b,我们进入S3。如果我们在S2读d,我们就进入S4。
如果我们在S3中读c,我们进入S2。
这些规则不能处理那些字符串
CD 处理完成后是
The string will be tokenized as 00/011/01.
The string will be tokenized as 011/00/100.
挑DFA
这里我觉得是,这个他都满足nfa和dfa
12题 挑选NFA ,有空跳
排除DFA即可,不能有多个输入对一个,
也就是ABC
This automata has 4 states, S0, S1, S2 and S3. S0 is the start state, S3 is the accepting state. The Transactions are following: If we are in S0 and read 0, we go to S1. If we are in S0 and read 1, we go to S2. If we are in S1 and read 0, we go to S3. If we are in S2 and read 0, we go to S3. If we are in S3 and read 1, we go to S0.
This automata has 4 states, S0, S1, S2 and S3. S0 is the start state, S3 is the accepting state. The Transactions are following: If we are in S0 and read 0, we can go to S1. If we are in S0 and read 0, we can go to S2. If we are in S1 and read 0, we go to S3. If we are in S2 and read 1, we go to S3. If we are in S3 and read 1, we go to S0.
This automata has 3 states, S0, S1 and S3. S0 is the start state, S3 is the accepting state. The transactions are following: If we are in S0, we go to S1 with out consuming any input, that is an -move. If we are in S1 and read 0, we go to S3.
This automata has a state Si for every non-negative integer i: S0, S1... Sn, and so on. S0 is the start state and the accepting state. The transitions are following: If we are in state Si, (i>=0) and read 0, we go to state Si+1. If we are in state Si, (i>=1) and read 1, we go to state Si-1.
这个自动机有4个状态,S0,S1,S2和S3。S0是开始状态,S3是接受状态。这些事务如下:如果我们在S0中,读到0,我们进入S1。如果我们在S0读到1,我们进入S2。如果我们在S1读0,我们就进入S3。如果我们在S2读0,我们就进入S3。如果我们在S3中读到1,我们进入S0。
这个自动机有4个状态,S0,S1,S2和S3。S0是开始状态,S3是接受状态。这些事务如下:如果我们在S0,读0,我们可以转到S1。如果我们在S0,读到0,我们可以转到S2。如果我们在S1读0,我们就进入S3。如果我们在S2读1,我们就进入S3。如果我们在S3中读到1,我们进入S0。
这个自动机有三种状态,S0,S1和S3。S0是开始状态,S3是接受状态。交易如下:如果我们在S0,我们去S1没有消耗任何输入,这是一个移动。如果我们在S1读0,我们就进入S3。
对于每个非负整数i:S0,S1,这个自动机有一个状态Si。。。Sn等等。S0是开始状态和接受状态。转换如下:如果我们处于状态Si,(i>=0)并读取0,我们进入状态Si+1。如果我们处于状态Si,(i>=1)并读取1,我们将进入状态Si-1。
CS-143 Week3 Parsing & Top-Down Parsing 【解析器&自顶向下的解析器】
05-01: Introduction to Parsing (5m31s) 【解释器介绍】
正则语言被广泛使用的最弱形式语言
许多应用
但是,有很大一部分相当重要的但无法以正则表达式或者有限自动机表达 的语言
元素在许许多多括号之中,也包括ifelse的嵌套
这些不能够被正则处理
正则可以表达什么
正则其实也就是自动机,这里举一个简单的双形态自动机来解释正则语言和有限自动机的局限性
读入奇数个1 我们处于最终状态
读入偶数个1我们处于开始状态
比如我们输入1111111
自动机不会记住字符串长度,他也不知道你经历了几次最终状态
有限自动机只能表达一些 对k取模count mod k (k是机器中的状态数)
但是不能对任意数来做取模
因此如果需要识别数学操作的表达式语言 例如
识别所有的() 中的字符串并做计算操作
parseing 可以做什么
它可以讲词法分析器生成的词法单元序列作为输入,并生成程序的解析树
在cool语言中,这个是一个表达式,将他输入到词法分析器中
词法分析器会产生这个词法单元序列 作为一个输出
解析器会生成这个嵌套明显,结构明确的解析树
Summarize
词法分析器讲字符串作为输入,并生成token(词法单元) 作为输出
然后解析器 把token当做输入,并生成程序解析树
有些时候,解析树是隐式的,虽然大部分编译器会构建显式解析树
现在的解析器通常把词法分析和解析放在一起
05-02: Context Free Grammars Part 1 (12m38s)【上下文无关法】
并不是所有的token字符串都是一个有效的程序
解析器必须告诉用户区别,它需要知道,那些有效,哪些没效果,并给出错误信息
我们需要一种方式来表述有效的token字符串
然后需要某种算法来区分有效token字符串和无效token字符串
![]()
编程语言具有自然的递归结构
例如在cool中,我们需要一个用来表示多个条件的判断选择表达式
也就是if和while 表达式
if expr then expr else expr fi
while expr loop expr pool
这些表达式本身由其他表达式递归组成的
if条件表达式,由then分支和else分支
while中,判断是一个表达式,循环体也是一个表达式
上下文无关法能自然的用域描述这种递归结构(recursive structure)
上下文无关法在形式上由如下组成
一组终端 T
一组非终端 N
一个起始符号 S (S是非终端之一)
一组产生式 (ps:这个可以叫做上下文无关法的规则)
一个产生式 指的是 一个符号跟着一个箭头,紧接着一串符号(x->Y1…YN)
这些符号有一定的规则,例如
箭头左侧的x必须是非终端符号(非终结符)x∈n
箭头右边的每个Yi可以是非终端符,也可以是特殊符号epsilon
也就是Yi ∈ N∪T∪{epsilon}
上下文无关法的例子
使用上一次的例子
一种可能是一对括号中间有一个字符串
S ->(s)
另一种可能就是括号里面是一个空的字符串
S->epsilon
我们的非终结符是N = {S}
我们的终结符是T = {(,)}左括号和右括号
开始符号是什么?是S,因为只有他一个非终结符
箭头左边都是非终结符,只要有式子产生,非终结符就会产 生
对于产生式
对于特定的上下文无关法,括号中的一组为产生式
productions can be read as rules
产生式可以当作规则来使用
比如S->(s)
这个产生式,我们无论在哪儿看到这个S都可以使用箭头右边的字符串符号进行替代
1.begin with a string with only the start symbol S
刚开始,我们只有这个开始符号–字符串S
2.replace any non-terminal X in the string by the right-hand side of some production X->Y1…Yn
我们替换为任意一个在右手边出现的非终结符字符串
例如可以用Y1..Yn 替换X
3.repeat(2) until there are no non-terminals
我们不断重复第二步,直到字符串中没有任何非终结符的存在,只存在终结符
example
一个推导过程
我们有一串符号
有一个产生式
进行了替换,这只是第一步
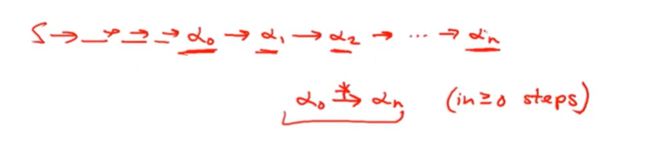
如果想要执行多个步骤 例如
也就是α-*->αn α0 经过0步或多步改写,最终得到αn (*号代表0个或多个步骤)
正常来说,我们从一个开始状态,会一步一步转换为其他字符串
finally
我们可以定义上下文无关法
上下文无关法L(G)有一个开始符号S,这个上下文无关法的语言将是符号字符串a1到an
对于所有的αi来说 αi是G的一个终结元素,T代表G的终结符集合
开始符号S代表a1...an 也就是我们推导的所有终结字符串都可以 以开始符为开始
terminal
terminal 也就是终端,终结,就是说,一旦这个字符串中包含了终结符,那么就没有规则可以进行替换他们
也就是一旦终结符出现,他就是这个字符串中无法改变的存在
在编程语言和上下文无关法的应用程序中,终结符是我们使用上下文无关法进行语言建模的标记
a fragment of cool
尝试使用上下文无关法,编写一段cool
if的表达式
EXPR -> if EXPR then EXPR else EXPR fi
在这个产生式中,我们将这些非终结字符变为大写,终结符都是小写
或者是while的表达式
EXPR -> while EXPR loop EXPR pool
最后一种可能性是他可能是标识符id
EXPR -> id
实际上会有很多很多可能性和其他很多很多情况
因此,对于同一个非终结符,我们会有许多的产生式
通常使用语法把他们拼接在一起 这里使用|
这样可以说EXPR -》 是右手边所有元素对应的非终结符
三个产生式组合在一起
some elements of the language
我们查看一下上下文无关法的一些字符串
单个标识符id就是一个有效的cool表达式
这里的产生式为EXPR -> id id(单个变量名)
我们可以直接将开始符号直接带到终端字符串中
示例:if表达式
if id then id else id fi
类似的,我们也可以对while进行操作
while id loop id pool
用产生式右边的替换左边
更复杂的表达式if+while
if while id loop id pool then id else id fi
if+if 内嵌if
if if id then id else id fi then id else id fi
simple arithmetic expression
我们再来看一个例子,简单的算术表达式
有一个开始符号,唯一的的非终结符E
E -> E+E|E*E |(E)|id
这个就是一个关于加,乘,括号运算以及变量名的一个语法
单个变量名(id) 就在上面这个语法中
id+id 同样在这个中,
id+id*id
(id+id)*id
the idea of a CFG is a big step
虽然上下文无关法能让我们在解析器中去表达想要的内容,但是仍然需要一些东西
在这个语言中,上下文无关法只能给出是或否的答案,一个字符串是或者不是这个上下文无关法中的,我们仍然需要一种在input(输入)处构建解析树的方法
我们必须要能够优雅的处理报错
我们需要实现上面两步,才能够真正实现上下文无关法
上下文无关法的形式很重要
这个工具通常对特殊语法很敏感,
这里的意思应该是:开始符和结束符都是限定的,不能够任意进行修改
05-03: Derivations Part 1 (7m07s)【推导】
推导就是,我们从开始符号开始,通过一系列产生式的替换,
当然也可以使用不同的方式而不是线性的替换顺序来 推导
我们可以做一个树,一个非终结符X,当我们替换X的时候,可以通过X的子节点来表示,也就是这些子节点可以用来替换这个产生式规则中左手的X
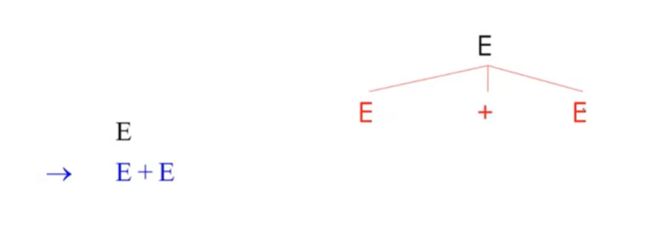
example
我们想要构建一个树
也就是找个表达式或者输入字符串的解析树
首先根据我们的语法式子,第一个就是简单的加法
乘法
逐个替换id,
也就构建了解析树
parsing tree
首先,解析树的叶子节点上是终结符,非终结符则位于内部节点
叶子节点的中序遍历所得结果就是我们的原始输入,(先遍历左子树,然后访问根节点,最后遍历右子树)
我们这个例子中,只有一个非终结符E,所有的内部节点都是E,并且叶子节点都是终结符字符串,,我们对叶子节点进行中序遍历,就是我们开始的输入字符串
这个解析树中,* 号比+ 更优先
因为星号的树是加号树的子树,做加法前先做乘法
刚刚的推导叫做左推导,
每一步都将字符粗,替换为最左边的非终结字符
当然也有相同字符串的最右推导,我们都在替换最右边的非终结符
E 换成id,
最左和最右推导都有相同的解析树
当然还有其他的推导,随机选择非终结符进行替换之类的
summarize
我们不仅仅对于这个字符串是不是在这个特定的上下文无关法中,同时我们对解析树也感兴趣
一个推导有一颗解析树,一颗解析树有很多推导
最左和最右推导,在解析器的实现中是比较重要的
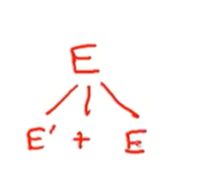
05-04: Ambiguity【歧义性】
这个字符串有两个解析树,通过解析树去反推产生式
最后把id替换了
![]()
我们发现,两个截然不同的解析树,推导出了一样的产生式
两种推导,生成了两种完全不同的解析树
这就是ambiguity 歧义,模棱两可
如果对于某个字符串有多个解析树,那么这个语法就是有歧义的
也就是,对于某个字符串有多个最右推导或者最左推导
也就会有截然不同的解析树
语法就有歧义
而且,对于有一些程序,如果有多个解析树,那么我们就需要使用编译器对程序的两种歧义进行选择来生成代码
当然,我们不希望出现歧义,编程语言中不希望出现模棱两可的地方
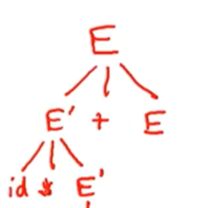
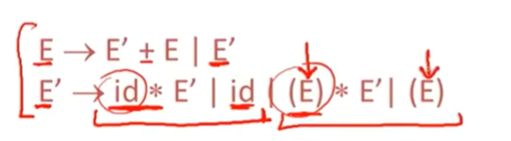
消除歧义
最直接的方法就是重写语法
我们的字符串仍然是id*id+id
我们从E开始,E不再生成一个+或者*号
我们讲语法分为了两组产生式,两个非终结符
E’ 负责乘法E负责加法
我们刚开始必须选用E'+E没有其他写法
我们看E‘的产生式,它能够生成id×其他东西 E’的乘法需要生成优先级表达式,但是带括号的优先级表达式和我们尝试解析的字符串不匹配也就是(E)*E' 我们只能使用 id * E'
为了匹配字符串,E‘ 只能替换为id,这里只有一个产生式可以做到
夹在*号和+号之间的元素
那么剩下的一个E怎么办
E 变E’ 在变id
我们将产生式分类,一个处理加法一个处理乘法,每个运算符都有一个非终结符
E 用来处理加法,
E -》 E' +E -> E'+E'+E -> E'+E'+E'+E'+E-> E‘+E'....E'
任意数量的E‘相加,停止后,我们把最后一个E转换为E’
E’的前两个产生式用来处理乘法id*,后两个产生式用来处理括号
E'->id*E'->id*id*E'->id*id*id*id*E'->id*id*id...*id
或者我们生成带括号的
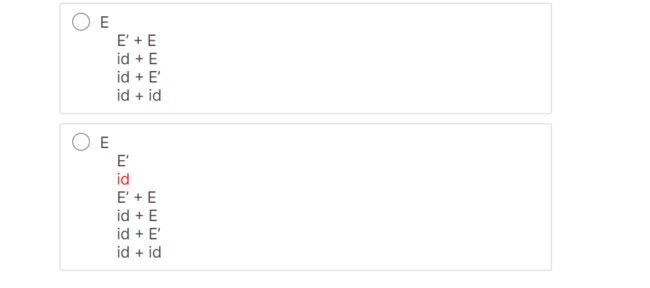
消除歧义的做法:
所有加法必须是在乘法操作之前生成的
乘号将比加号在解析树的更下方(更深处)
E’在加法操作内生成乘法操作
这个语法强制乘法优先级比加法高
在括号表达式的是E 而不是E‘
因为括号可以提高优先级,括号里面可以是加法
通过重写语法,右边的解析树就无法使用了,左侧的解析树会有一定的更改
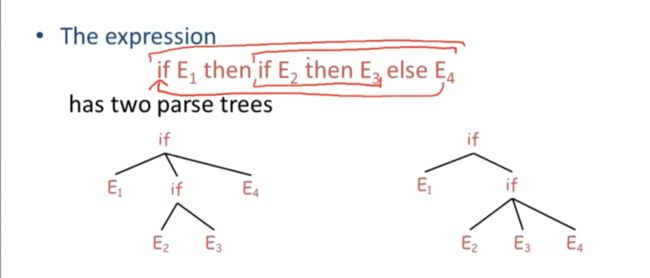
example
我们这里通常会有if then else
同时也会有if then 没有else的产生式
也可能有其他other表达式
这个表达式也会产生歧义,
也就是两种解析树
1- 可能是if E2 then E3 一组,是内部的,,if E1 then else E4 为一组
2- 也可能是if E1 then 一组 if E2 then E3 else E4 一组
当然我们想要的是第二种,也就是需要规定,else和离他最近的if-then相关联
我们的if语句会分为两类
一种是被匹配的,将所有嵌套在其中的then-else语句与if匹配
一种是没有被匹配的,就是在内部有一些then
if-then-else 是最常见的if匹配,在他的分支中,任何内嵌的if语句都必须要有匹配的else 如果有非if-else的构造,也能够被认为是一个已经配对儿的if
都是MIF 配对儿过的if
那么关于未匹配的if呢
一种可能就是他是一个未匹配的if没有else 也就是if-then
另一种就是if -then-else then 里是MIF 也就是匹配的if,else后的才是UIF
这里是为什么呢?
如果我们的这里不是MIF 也就是 UIF, 那么里面就是if then 必然就会和后面的else 就近原则匹配在一起
那么我们来回顾之前的表达式
else是匹配了最近的if then
有歧义的语法自动转换为一个明确的语法,这是不可能的
必须我们手动来做
一种方法就是我们会以某种方式将这种模棱两可的特性纳入其中,这能让我们有更深入的自然语义
另一种就是、我们需要一些消除歧义的机制
当多个解析树出现的时候,值出哪个解析树是我们想要的
当然我们不会去重写语法,我们会使用更自然的歧义语法,配合消除歧义机制来做,一些工具也会提供消除歧义声明
最常见的就是优先级和关联性声明
即使只有一个中缀,也会产生歧义
这里 我们定义加号为左相连性 是BISON中的表示法,
有一个更复杂的语法, 有加法,乘法,
我们定义多个关联性 和优先性
乘法排在加法后面也就是乘法具有比加法更高的优先级
06-01: Error Handling (13m03s)【错误处理】
编译器有两个职责,通过程序代码生成更低级的代码
另一个就是 给错误处理程序提供良好的反馈,检测无效的程序
针对不符合语法的无效代码不进行编译
比如词法错误,使用了根本不会再该语言中出现的字符,会在词法分析中找到
语法错误 每个词法单元能够正确识别后,组合起来,不能生效,这种情况就是解析错误,
语义错误,类型检查器就会进行捕获
剩下的问题由使用者解决
处理错误需要什么
1- 需要编译器能够准确清晰的报告错误
2- 编译器能够从错误中很快的恢复过来
3- 不应该让错误处理机制来降低有效代码的编译速度
error handling
我们使用紧急模式和错误产生式
旧的方法是:自动局部或者全局校正 过分追求完美
紧急模式比较简单,当有一个错误被检测到时,解析器开始抛弃token知道在这么语言中找到一个作用明确的token为止
编译器会自己重启,从那个新的token继续工作
这个寻找的这些token被称为同步token(synchronizing token)
也就是说,当遇到问题的时候,通常的解决方案就是试着跳到语句的末尾或者函数的末尾
panic example
例如(1++2)+3
这里多了一个+号,
解析器读取到第二个加号的时候,就卡住了,这里先忽略自增
他切换模式,然后开始不断地丢弃输入的字符,直到遇到解析器能够识别的字符,这种错误的恢复就是,有一个规则,挑倒下一个数字,然后试着继续往下走
我们就将第二个+号忽略了
bsion
bison是一种广泛使用的解析生成器,
bison有一种被称为error的特殊终结符,可以用来描述多少输入需要调过
bison的产生式为
E 可以是一个数字,可以是两个E之和,或者两个表达式相加,括号表达式,
如果不是这三种normal的表达式,那就是 error(bison特有的)
error int 就是抛出所有的输入,直到遇到下一个int数字,同理,括号表达式中有错误,直接忽略内部,继续解析
error production
另一种策略 错误产生式
也就是编译器设计者可能知道代码中有一些常见错误,使用增强语法,在遇到这些错误是生成相关的错误结构
也就是将程程序员已知的错误指定为语法中的替代产生式
5x一般来说代表5*x但是计算机不会识别
因此增加一个产生式就可,E->EE
缺点是 我们的语法比较复杂,难维护(但是在实践中比较多)
最后一个策略 错误更正
一些错误编译器会帮你改,找到合适的替换程序
可以进行一些token的插入和删除
这里就是想要将edit distance 编辑距离最小化,也就是(a转换为b最少操作次数) 这是一种量化测量方式,用来判断一个程序是否接近程序员所提供的源程序
或者可以在一定范围内详细的搜所,来找到与源程序相近的所有可能的程序
exhaustive(详尽的)
缺点就是
比较难实现,降低对正确程序的解析速度,因为我们需要存储足够多的状态(替换规则) 让我们去搜所,进行距离编辑保证最小化改动
意思表达的相近 可能并不会被程序员接收,因为可能是不符合预期的
错误更正做的比较好的就是PL/C编译器
PL代表PL/1编译器,C代表东阿是康奈尔大学
past 过去的错误处理
在过去,
重编译非常的慢,可能你一跑就是一天
一旦由于你输入错误一个关键字,编译器就会尝试努力找到一个可运行的程序,如果修正小,就会减少你的时间,
在现在,
重编译很快,
一个周期一个bug,发现并且修复第一个错误,
06-02: Abstract Syntax Trees (3m50s)【抽象语法树】
解析器用来跟踪一系列词法单元的推导
但是 编译器还需要知道程序所代表的含义
编译器需要一种实际的数据结构来告诉他程序中有什么操作
解析树并不是我们想要处理的数据结构,我们是在抽象语法树的数据结构上面进行工作
abbreviated(缩写)
抽象语法树缩写为AST
这里有一个关于整数的加法运算和括号表达式
有一个输入字符串,经过词法分析后,得到一个词法单元序列以及对应的词素
接着传入解析器,就会构建出一颗解析树
解析树十分的冗余
E 转换为int 就不是必要的
因此选用AST来将这些垃圾信息进行压缩
我们有两个加法,三个参数
他们之间的关联性就是看那个加号在另一个里面
我们也没有任何无关的非终结符元素,也没有括号
AST 取消了具体语法的细节,保留了足够的信息,能够很好的表示程序要做的事情,并进行编译
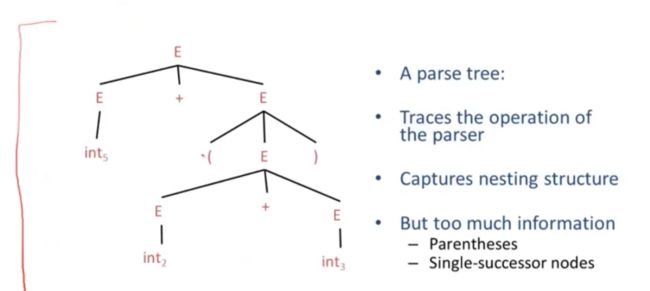
06-03: Recursive Descent Parsing (6m35s)【递归下降解析】
递归下降解析是一种自上而下的解析算法 Top-down
在自上而下的解析算法中,解析树是从上面开始构建的
从根节点开始,按照从左到右的顺序
终结符元素会按照他们在词法单元字符串中出现的顺序进行排序
例如t2 t5 t6 t8 t9 就会构建如下的图
example
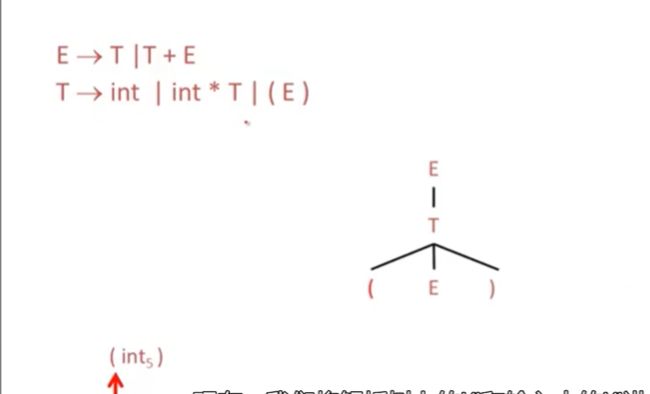
整数表达式的语法
输入是一个(int5)
我们使用递归下降策略解析这个表达式
我们从一个非终结符元素开始,也就是根节点,尝试E-》T ,不行的话尝试E-》T+E
当一个产生式失败的时候,就需要替换为其他的产生式
我们首先尝试采用E->T
然后T->INT
但是我们的输入是括号,因此不能和这个解析树进行匹配,我们就需要回溯几步,如果是(E) 这个就可以进行匹配了
我们回溯一步,接着采用
T->INT*T
接着使用int和(int5) 进行匹配,很明显,不匹配,
接着和(E) 匹配
括号匹配到了
接着我们需要扩展括号里面的E
同样逐个匹配,然后最终指针指向字符串的下一个位置,
也就是我们接受这个解析树,解析器会成功结束
quiz
06-04: Recursive Descent Algorithm (13m28s)【递归下降算法】
背景提要
TOKEN 代表了一系列的词法单元 用来写代码用,比如有INT,OPEN,CLOSE,PLUS,TIMES 等token
需要一个全局变量指针,next,指向下一个输入的token
我们首先定义一些define,用来匹配输入中所给定的token的函数
bool term(TOKEN tok){return *next++ == tok;}
这里返回的是boolean值,如果我们传入的token和输入的相匹配,就是true
无论是true还是false,指针都会向前
第二个定义的函数是,对S的第n个产生式进行匹配
bool Sn(){...}
这个是用来检查里面是否有与S中产生式成功匹配的函数
第三个就是验证匹配S中所有产生式的函数
bool S(){...}
也就是有任意一个产生式能够匹配输入,我们就解析成功
对于每个非终结符元素,我们都有两类函数
一类就是对于每个产生式都有一个对应函数,他检查这个产生式是否能和这个输入匹配上
另一类就是将关于这个特定非中介元素的所有产生式组合在一起,然后检查这些产生式中是否有任何一个能和输入进行匹配
example
这个语法的第一个产生式是E->T
我们想一个函数,判断该产生式能否匹配某些输入
bool E1(){return T();}
首先我们写出函数E1 它用来处理第一个产生式E,仅当产生式成功匹配输入的时候返回true
这个函数如何匹配输入的呢?
也就是在当T的部分产生式匹配输入的时候,他才能匹配一些输入,也就是T()函数
T()返回结果为true的时候,E1才会返回true
对于第二个产生式for production E->T+E
bool E2() {return T() && term(PLUS) && E();}
首先函数T() 必须要匹配一些输入,T中的一些产生式必须匹配输入中的一部分内容,才可以接着走下去
我们必须在匹配T的输入中找到一个带+号的输入,也就是PLUS
如果加号匹配了,对于E()所代表的产生式需要匹配输入中的一部分
&& 与运算 在C和C++中是按照从左到右的顺序来计算
先T() 执行到找到后,执行trem(PLUS) 在执行E()
最后一个产生式E,这里需要回滚
我们需要E能够匹配更多,也就是为他写一个备选函数
bool E(){
TOKEN *save = next;
return (next = save,E1()) || (next = save,E2());
}
输入需要匹配这两个中的一个
我们在回滚中需要考虑next指针,因此我们使用局部变量save,用来记录我们最初next的位置
如果E1匹配成功,E2就不会去匹配,会在||停止
E1的next=save这句为了工整才写,没有其他作用
E1返回false,第二部分为true,就需要恢复next,
如果E返回true,就需要去找其他方法了,
Functions for non-terminal T
对于非终结符T,有三个产生式匹配函数
第一个产生式就是
bool T1(){return term(INT;)}
也就是T->int
去匹配terminal(int)
因此我们接下来输入的就是整数才会进行匹配
第二个产生式就是T->int*T
bool T2(){return term(INT) && term(TIMES) && T();}
因此我们需要匹配的就是int,后跟一个*,在跟一个T这个产生式的内容
第三个产生式是T->(E)
bool T3() {return term(OPEN) && E() && term(CLOSE);}
先匹配左括号, 然后匹配函数E能够匹配的,然后匹配右括号
将他们三个放入函数T() 当备选
启动解析器
初始化指针,调用E()
递归下降解析器很容易手动实现
summarize
最上面是我们的两个语法
下面是我们根据递归下降的所有代码
我们的输入是(int)
指针从开始记录token,(
然后我们构建解析树,从E开始推导,
接着尝试E1,调用了T
T又去调用,后面的三个
T1失败。T2失败,T3成功
然后指针指向了int
然后我们重新调用E,E调用了E1
只有匹配了T才能够匹配E1,因此这个树从T接着画
在T中,逐步尝试,匹配了T1,
匹配右括号后,成功解析字符串
quiz
06-04-1: Recursive Descent Limitations (6m56s)【自顶向下递归局限性】
从上节课开始,我们
假设有一个int,我们如何匹配呢?
首先E()->T()->T1()
T1识别int返回true,
那么我们假设有一个int*int 怎么匹配
E()->E1()->T()->T1() 然后我们匹配到了int,T1返回true,逐步向上逐步true,然后匹配字符串结束,然后rejected
这里是为什么呢? 因为你没有匹配到语法,
我们如果匹配的是T2() 那么肯定是一个乘法,虽然有回滚,但是也是在第一个T1 也就是匹配int,失败以后,才会去尝试下一个T2
这里的问题是如果找到一个能应用于非终结符元素的产生式的话,之后就没办法进行回滚了,
因此,一旦针对x的函数有返回值,就结束了,因此递归下降算法,并不是完全通用的,
展示递归下降是因为,递归下降很容易实现,但是有局限性
我们可以看到,根据一个给定的语法,去设计一个而解析器是非常简单的,而且适用于相当大的一类语法,它适用于任何语法,在该语法中,任意一个非终结符最多使用一个产生式就可以完成解析,可以用来构建我们自己的语法,在任何情况下都可以使用递归下降算法解析
我们需要优化/重写这个算法
06-05: Left Recursion Part 1 (8m05s)【左递归】
首先有例子S->Sa
我们写两个函数,就不需要去回滚了,只要s1成立,s就成立
但是,很明显,这里有问题,
输入字符串我们就调用s,s调用s1,s1调用s,无限循环
infinite(无限的)
原因就是 他是左递归,左递归语法是指具有非终结符的任何语法(就是对S解释中又包含了S这个非终结符)
如果从非终结符开始,就要做一系列非空序列重写,就需要循环调用,
![]()
+号就是重写很多次,我们无限次的对最左边的进行替换,对最左边的进行解析
我们就不能匹配任何输入,他从S->Sa->Saa,一直把最左边的s替换掉
递归下降的解析方式不适合左递归语法
左递归语法形式
S->Sα S->β
这里有两个关于S的产生式
也就是说,字符串的生成就是,一个β和后面任意数量的α
S->Sα->Sαα->...->βααααααααααα。。
我们这个字符串,我们可以看到, 先生成的α,第一个β是最后生成的,也就是为什么递归下降不能够生成字符串的原因,
我们可以通过右递归,代替左递归,
重写使用右递归,
第一个位置是β,S‘ 是代表一系列α,当然也可能是空字符串
s->βS'->βαS'->...->βααααααααααα
我们最后生成的两个字符串完全一样
我们会有很多产生式,有些是左递归,有些不是,
这些字符串从β开始,不包含S,但是后面会跟着0个或多个α
右递归来重写左递归,多一个S’
这并不是左递归最常见的形式,有其他方法来对在一个语法中的左递归进行编码
首先有一个看起来不像左递归的语法,
S->Aα|
A->Sβ
第一个产生式右侧甚至没有S,
第二个产生式右侧并没有A
这两个在语法中被称为非直接左递归
其实是一个左递归,因为S会变为Aα,然后又能变成为Sβα
花两步生哼另一个左侧有S的字符串
S->Aα->Sβα
因此在这个S返回之前,我们可以在最左位置是插入其他的非终结符来对他进行延迟操作
这个左递归能够自动消除,在龙书里面有实现的算法
summarize
在常见的解析策略中,他是很简单的一个例子,你能够通过使用递归下降来解析任何上下文无关法,但他不适用于左递归文法
因此必须消除左递归,实际上,人门通常手动消除左递归,
gcc的前端就是用的手写递归下降解析器
CS-143 Week4 Bottom-Up Parsing 【自底向上解析】
07-01: Predictive Parsing Part 1 (7m40s)【预测解析】
我们使用预测解析继续对自上而下的解析算法进行处理
预测解析和递归下降很像,依然是一个自上而下的解析器,
但是它能够预测该使用哪个产生式,永不出错,
这个解析器能够正确的猜出该使用哪个产生式来得到一个正确的解析
- 第一个“L”:left to right,按照从左到右的顺序处理输入的token序列
- 第二个“L”:leftmost derivation,从文法的最左边开始进行推导
- “(1)”:使用1个token来预测解析的方向(当然也有LL(n))
预测解析有两个特征:
1- 解析器会去看接下来的一些token,会采用向前看的方式来尝试值出该使用哪个产生式 lookahead 但是限制于语法形式很固定的情况
2-解析器不需要回滚,能够自己肯定所要使用的产生式
预测解析器接受一种LL(k) 的语法
第一个L 按照从左到右的顺序读取
第二个L代表了最左推导,使用最左推导构建解析树,
k代表有k个需要向前看的token k可以是任意数 我们只讨论1的情况
在递归下降的规则中,每一步都有很多的产生式供我们选择,必须要去回滚来撤销错误的选择,
在LL(1)解析器中,每一步只会有一个可供选择的产生式来进行使用
如果有一个输入字符串,这个字符串中,有一些终结符号w和一个非终结符号A,后面可能还有一些其他字符串
wAβ 下一个输入的token是T
这里有一个产生式A->α 我们只能使用这个,甚至这个产生式都可能会不成功,
但是在LL(1) 解析器中,始终会有最多一个可供我们使用的产生式
在这个例子中,我们会将字符串重写为wαβ
T的前两个都是int开头,如果说输入流中有int,并不能帮助你判断使用这两个产生式中的哪个去使用,
只是向前看一个token的话,没有办法再这两个产生式中进行选择,
我们对E也有同样的问题,不光是T
E的两个产生式都是以非终结符T开头
仅向前看一个token,去判断,并不容易
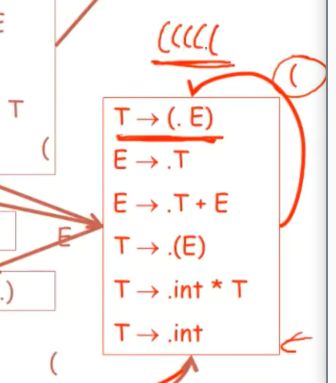
我们需要改变语法,上面的语法,对于预测解析是不能接受的
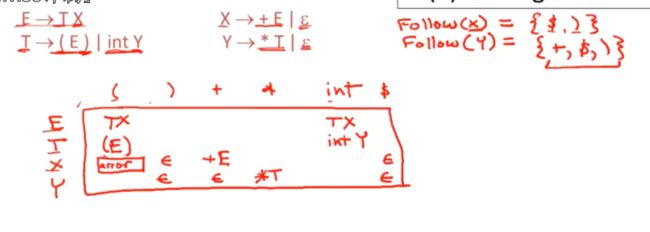
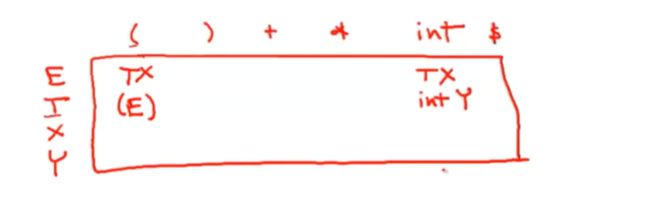
我们提取左公因子
提取左公因子的思路就是消除一个非终结符的多个产生式的公共前缀
E->TX
X->+E|epsilon
这里引入一个新的非终结符X用来处理剩下的部分
这样会延迟我们选用哪个产生式
第二个
T->intY|(E)
Y->*T|epsilon
(E) 不受影响,所以可以写在第一步里面
这个是我们提取左因子之后的语法,
使用这个语法构建解析表
example
第一个TX格子的意思是找到当前非终结符为E,同时下一个输入是int的格子
我们使用产生式 E->TX
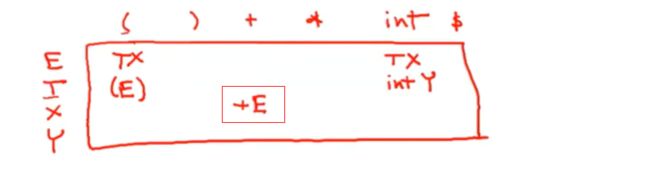
当左侧是Y,下一个是+号
唯一解析的就是不生成任何东西,如果想要解析这个字符串的话,需要拜托T并且而移动到另一个非终结符上,也就是Y之后的最左非终结符
这里有很多单元格都是空的
最左终结符是E,token是* 那么没办法选择任何产生式,就会遇上解析错误
解析表进行解析的算法
我么你需要看最左非终结符S,同时要看下一个输入token,通过解析表查找(S,a)这一格的产生式,而不是通过递归函数去构建解析树
我们使用栈的方式来记录边界
解析树上我们会有一些还未展开的非终结符,他们始终处于当前解析树的叶子节点上,
当然还有一些未被匹配的终结符,他们会被记录在栈中,
这个栈的重要属性就是把最左终结符或非终结符始终放在栈顶
因此我们试着去匹配的终结符还是尝试去展开的非终结符,他们始终处于栈顶
如果我们找到空单元格,直接拒绝解析
如果我们到达输入的末尾的话,就会有一个空的栈,这样就会接受这个解析,意味着没有待处理的不匹配终结符或者为扩展的非终结符了
这个是他的算法,我们将栈初始化,里面有开始符号S和特殊符号$
符 号 并 不 属 于 字 符 表 中 的 一 部 分 , 我 们 将 字 符 表 进 行 了 扩 展 , 引 入 了 新 符 号 ‘ 符号并不属于字符表中的一部分,我们将字符表进行了扩展,引入了新符号` 符号并不属于字符表中的一部分,我们将字符表进行了扩展,引入了新符号‘`
$ 标记了栈底位置,也就是一个输入结束的标记
完成匹配后,我们就是处于输入的末尾
上面整个处于一个循环之中,知道我们无法重复这些代码,或者直到整个栈为空
这里有两类
第一类是假设栈顶元素处理终结符t,如果栈顶终结符匹配了输入中的下一个元素,我们就移动到下一个元素,否则调用error,没有回滚
第二类是假设栈顶元素非终结符X,根据解析表来查找非终结符x和下一个输入字符所对应的产生式右手边的内容
我们将解析树中x的子节点压入栈内,
这个是我们的栈,和输入的字符串,产生式的相关匹配
从E开始,同时构建解析树
接着,E被弹出,TX被压入
07-02: First Sets (14m02s)【first集】
如何构建LL(1)解析表
我们需要知道一个给定的非终结符A,给定的输入t,T[A,t] =a
第一种情况,如果α可以推导出t在第一个位置,α经过多次推导
推导出t∈first(α)
tips:
产生式S->ABCD,A->a|epsilon ,B->B|epsilon,C->c,D->d
a,b可能为空,就是c了,不会有d,
如果在A,B,C 中,A生成了一个t,那么就没有后续bc产生式了,
另一种情况,A最为最左非终结符,t作为下一个输入,我们会使用α替换A,即A->α,
我们要考虑的就是α无论经过多少次推导都无法得出t,t不是first(α)中的元素
我们依旧能够解析,
我们提供一个产生式α->*epsilon
α通过0次或者多次推导,变为epsilon
并且在语法中,t能够紧挨着A,
这里t是属于Follow(A)的
A不会生成t,t是在A之后推导出来的
这个A之后的t和A生成的元素没有任何关系
first集合的计算
对于任意字符串,如果经过多次推导后,X能够在右手边第一个位置推导出t的话,那么我们就说t是一个终结符,并且是First(x)中的元素
如果X通过0或多次推导后能得到epsilon,我们也会说epsilon是first(x)中的元素
算法简述 (algorithm sketch)
对于所有的终结符,他们的first集由该终结符的元素组成
非终结符
这里匹配每一个非终结符 递归的算出每个符
第一个,X-》epsilon 所以epsion是first(x)中的元素
第二个,x-》a1…an 右边都是非终结符的情况下,也就是a1…an经过0-n次变化都能够变成epsilon,这种情况下,epsilon才能够属于first(A)
另一种情况
first(α) 属于first(x) 的子集
当a1.。。an都能转换为epsilon的时候
x通过0-n变为了α,
第一个计算终结符的first集,第二、三个计算非终结符的first集,
example
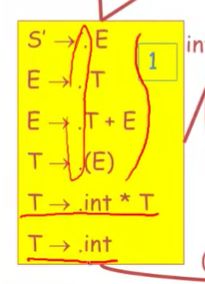
我们先计算终结符的first集
First(+)={+}
First(*) = {*}
非终结符的first集
我们知道,first(T)中的元素同样是first(E)中的元素、
first(T) ∈first(E)
first(T) 是first(E)的子集
首先得推出firstT,T的产生式中,右侧第一个位置生成了终结符(或者int
First(T) = {(,int}
那么firstE是什么,如果T能够变成epsilon的话,firstx能够成为firstE的子集,我们得出了,firstT的集合,epsilon并不在其中,也就是说firstT至少会生成一个终结符,X永远不会是firstE,因此,firstT和firstE相等
First(E) = first(T)
First(X) = {+,epsilon}//右边表达式的第一个就是终结符,所以填进去
First(Y) = {*,epsilon}//同X
07-03: Follow Sets (17m05s)
这里给了定义,Follow集,经过一些推导, 该终端t可以紧接着在符号X之后出现,所有的这些t组成了follow集
如果我们由X->AB,那么first(B) 属于follow(A)
X->AB->Atβ
这个t是first(B)的元素,同时也属于Follow(A)
当有两个相邻符号的时候,第二个符号的first集中的元素是第一个符号的follow集合中的元素
产生式末尾字符
如果B能够编成epsilon 或者能偶小时,A就会作为产生式的末尾符号
Follow(X)成为了Follow(A)的子集
S->xt->ABt ->At
那么$符号在哪个集合中呢,是在开始符号Follow集合中的元素
algorithm sketch 算法概述
前两个就是固定的,没什么考虑的,
第三个
如果产生式的后缀β可以被消除,也就是epsilon,左边的A 元素的follow集就是followX的子集
example
我们计算这些语法的Follow集
根据定义,$肯定是FollowE的元素
我们找E在哪儿使用过
T->(E)
E在终结符后,所以)是followE的元素
FollowX属于是FollowE的子集
如果我们想要算FollowE 就需要先算FollowX
E->Tx
这个里面,左侧符号,FollowE 是FollowX的子集
所以FollowX = FollowE
我们接着计算FollowT
只有两个地方使用了T
FollowT = {+,$,),}
E->TX->T+E因为我们不考虑epsilon,所以不做补充,
在E->TX中,因为X可以被消除,FollowE中的任何元素同样是FollowT
这个里面,T在最末尾,因此FollowY中任何元素也都是FollowT中的元素
FollowY也是FollowT的子集
为了计算FollowT 因此我们需要知道FollowY
![]()
Y出现在右侧末尾,因此
FollowT 是FollowY的子集
因此FollowY = FollowT
Follow Y = {+,$,)}
上面计算完了所有的非终结符Follow集
接下来我们计算终结符Follow集
Follow('(') = 就是First(E) 中所有的元素
FirstE 和FirstT相同,First有一个( 和int
在这里面
Follow(T)中的任何元素都是Follow(’)’) 的元素
Follow(’+’) 用在这里,因此FirstE 中的任何元素都是Follow+中的元素
FirstT中的元素都是 Follow(*) 中的元素
Follow(int) = {}
Follow(int) 会包含FirstT中的所有元素,*,+,$,)
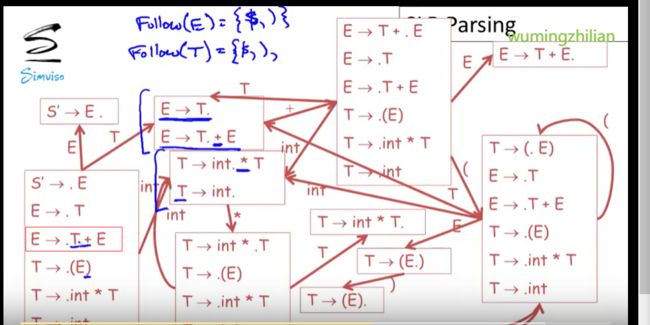
07-04: LL1 Parsing Tables (14m41s)【LL1解析表】
语法G中的一个产生式A->α
当我们遇到,A是最左非终结符,t是输入中的下一个token的话,这个表T[A,t] = α
第二个,t是follow(A)中的元素,并且产生式右手边的内容是epsilon,A是最左非终结符,t是输入中的下一个token的话,这个表T[A,t] = α
最后一种情况,为了消除A,epsion是First(α) 的元素,并且在一个推导中$ 能跟在A的后面
上面就是构建一张解析表的流程/规则
example
我们来构建解析表
列名,肯定就是终结符,非终结符用来当行名(ETXY)
我们只需要考虑他在产生式右侧的第一个位置能生成什么即可
当然这个就是T的first集合中的元素,也就是(,int
当我们使用T->(E) 的时候
T是最左非终结符,)是输入中的下一个符号
我们使用(E) 来替换T,
另一个产生式,T是最左非终结符,int为输入,
当我们选用X->+E
左边的非终结符是X,右侧第一个位置是+
Y也一样,当Y是一个非终结符的时候,我们尝试把他展开,如果输入* 我们使用产生式Y->*T
我们考虑epsilon ,
我们为了知道什么时候使用产生式X->epsion 就需要知道Follow(X)中有什么,上节课写了
Follow(x)
需要先找那里用到了X
E->TX
在右手边,他就是FollowE的元素,
FollowE有什么?
E是开始符号,$,")" 都是followE的元素
![]()
接着Y同理,
FollowT中的任何元素都是fOLLOWy的元素
followY中包含firstT的元素,因为X能跟在T后面出现
当输入末尾的时候,我们把X替换为epsilon
如果栈内有一个”)“ 我们就把X替换为epsilon 因为x自身无法生成一个),我们消除了X,栈内就能生成其他符号的语言
这就是followX
Follow 同理
空白单元格对应什么呢?
当然就是解析错误,
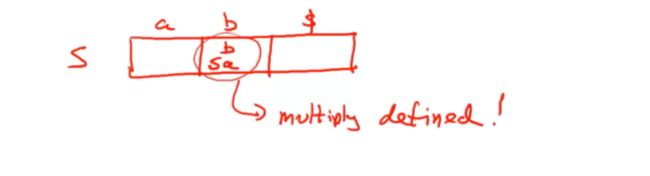
我们来思考一下我们为一个非LL(1) 语法构建LL(1) 解析表时会发生什么
S->Sa|b
为了构架这个语法的相关解析表,我们需要知道first集,和follow集
First(S)产生式的右边第一个能产生b,并且没有任何可能生成epsilon
First(S) = {b}
Follow(S)={$,a}
因为S是开始夫,所以$是followS的元素,因为第一个产生式中,a跟在S后面,所以a是followS的元素
构建解析表
比较小。
如果我们在输入中看到b的话,我们就会使用S->b
同时有多种选择,Sa
这就是一个多重定义的单元格
如果我们想要展开的最左非终结符,也就是栈顶元素为S,b是我们下一个输入符号的话,
这张解析表并不会明确的告诉你走哪里,这就是不是一个ll(1)
如果构建解析表有多重操作,就不是一个LL(1)
LL(1) 的一个定义,检查这个语法是否是ll1的唯一方法就是去构建ll1 解析表,然后检查解析表中所有的单元格内选择是否只有一种
当然有很多语法不是ll1语法
比如,任何无法被提取左公因式的语法都不是ll1语法
任何左递归语法也不是ll1语法
任何语义混淆的语法也不是
如果向前看多个token也不是ll1
这些是可以快速判断的,
07-05: Bottom-Up Parsing Part 1 (7m06s)【自下而上的解析】
自下而上的解析不仅更通用,而且同样高效,而且是大部分解析生成工具所使用的一种首选方法,
自下而上不需要提取左公因子,因此能够回归自然的语法
我们仍然需要对+号和*号的优先权进行编码
example
string int*int+int
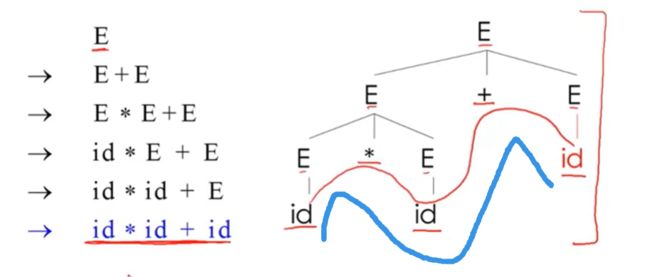
有关自下而上的解析要知道的第一件事就是他会进行归约,通过反转产生式,逆向替换,将字符串归约为起始符号
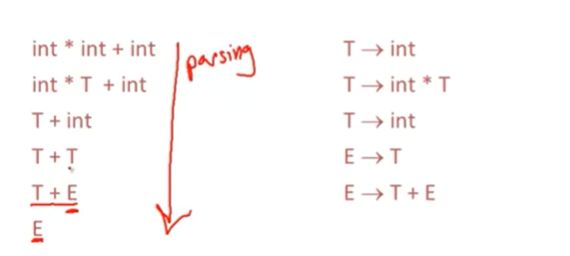
(tips:从具体元素开始逐层替换为上一级可处理的产生式,最后聚合为一个产生式,即为归约)
inverting :倒置
左边是字符串状态序列,右边是使用的产生式
我们进行逆向使用,我们在这里将int替换为了T
然后下一步,我们对子字符串int*t 替换为了T,
依此类推
最后我们以开始符号E结束
我们从底部向上读,其实就是一个产生式,逆向推导就是Reduction(归约)
事实上,编译器解析过程也是向下的,
如果我们从开始符号,往上看,他就是一个最右展开,
一个自下而上型解析器,将反向追踪一个最右推导
自下而上的解析器跟踪的是一个最右推导
他通过使用归约来代替产生式的推导,然后以反方向的顺序进行
左侧是归约过程,右侧是根据归约构建的解析树
![]()
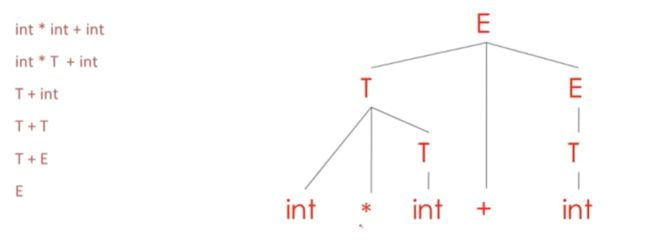
我们从输入开始,
通过展开当前叶子节点的非终结符来主键生成解析树
自下而上的解析树,从底部开始构建
总结,一个自下而上的解析器会以逆序追踪一个最右推导
通过将小型解析树结合在一起来构建更大的解析树
07-06: Shift-Reduce Parsing Part 1 (5m40s)【移位规约解析】
通过所有自下而上解析器所使用的主要策略(也就是所谓的移位规约解析) 来继续对自下而上解析进行讨论
上节课的重点,
假设我们有字符串αβw ,我们来思考下以为归约解析的状态
假设我们下一步归约是使用X对β进行替换
规定w是一个终结符
如果从最右推导来看,X必须是最右非终结符,也就是X的右侧不存在任何非终结符,w 所代表的也就必须是终结符token
这些最右非终结符右边的终结符再自底向上解析器视线中,恰好是未经检查的输入,
当我们读到X,w 是我们还没有读取到的输入,也就是未经检查的输入
我们通过| 来在已读部分和未读部分画一根竖线
竖线左侧是终结/非终结 都可以,但是在右侧,我们并不知道有什么,即使我们知道是终结符
为了实现自下而上解析,我们需要两种操作,移位操作和归约操作
一次移位操作就代表了从输入中读取一个token
我们可以将他解释为将竖线向右移动一个token的位置
yz是解析器还没有读取到的部分
归约操作是对竖线左侧字符串的右端末尾逆向使用产生式
如果有这样一个产生式A->xy,同时竖线的左边有x和y
我们使用产生式左侧来替换产生式右侧的内容
这就是归约操作
这就是上节课的例子,我们来展示归约操作和移位操作
第一次操作就是要进行一个移位
有一次移位,又一次移位
只允许我们去对箭头左侧的内容进行归约
执行一个归约操作前我们需要读足够多的输入
再来两次移位
到末尾了,不移动了,
就开始归约
事实证明,竖线左边的字符串能够由一个栈进行实现,
因为我们支队竖线左侧的字符串进行归约,
移位就是将token压栈
一个归约操作,将一些符号从栈内弹出
在一个给定状态下,经过多次移位或者归约,我们可能会得到一个有效的解析
特别是,如果移位或者归约操作是合法的话,也就是,既可以移位,又可以归约,就会有shift-reduce冲突,这个一般可以消除,通过优先级声明
解析器既可以读入token,压入栈内,也可以执行归约操作
如果归约操作由两种不同的产生式都可以做到并是合法的,那么这里就会由一种成为reduce-reduce的冲突
这表明语法出现了问题,比较严重,
08-01: Handles Part 1 (4m35s)【句柄】
回顾:自下而上有两种操作,移位操作,读取完一个token,并将竖线向右移动一个token
归约操作用产生式右手边的内容来替换产生式左手边的内容
竖线左边的字符串能够用一个栈来实现,栈顶元素使用竖线进行标记
移位操作会将终结符压入栈内,归约操作则会让栈弹出0个或多个符号
会将非终结符压入栈内,也就是该产生式的左手边的内容,
有个关键的问题,我们如何判断什么时候移位,什么时候归约呢?
当我们读取到int的时候
我们可以使用T->int 变成T|*int+int
但是没有T* 相关的任何产生式
因此,如果我们归约后再去移位,就很难了
移位的结果可能是T*int,T*int+,T*int+E
但是永远无法返回E,没法处理T*
我们不能一味地去归约,
即使栈顶元素是产生式右手边的内容,他也有可能是一个错误的归约操作
我们来看这个最右推导
S经过若干步变为αXw,再变成αβw
反过来就是解析器解析的方向,也就是归约的方向
总之,如果这是一个最右推导,αβ就是αβw的句柄
也就是说β归约为X是正确的
能够使用X替换β
句柄可以将进行归约操作的地方直观的展示出来
句柄就是一个古i粤电,可以允许解析器通过进一步的归约操作回到开始符号的位置,
tips:句柄包含了一个可规约的操作路径,
我们只想在句柄处进行归约,不在句柄处归约,解析器可能会卡住
我们怎么去找出句柄呢?(见下节课)
自底向上解析的第二个重要事实,在归约和移位操作中,句柄只会出现在栈顶,所有操作都在左侧,用栈足够
这里有一个句柄只会出现在栈顶的非正式证明,通过一系列归约操作做到的
初始为true,栈空,
当我们结束归约操作后,最右非终结符就会成为栈顶元素
也就是一个最右非终结符X,还有一个竖线,见图
由于是最右推导,也就是下一个句柄必须在最右非终结符右边的某个位置
下一个句柄必须包含X| 这些部分
因为我们无法对最有非终结符的左边进行任何归约操作
一旦我们的栈顶元素是这个非终结符的话,下一个句柄必然在他的右边某个位置
句柄永远不会出现在最有非终结符的左边
归约和移位我们永远不需要向左移动
08-02: Recognizing Handles (13m12s)【句柄识别】
坏消息,:解析的时候没有一种合适的算法,能够快速找出句柄
好消息:有heuristics(启发器) 可以用来帮助猜测句柄,对于相当大的一类上下文无关文法来说,这些启发器始终能够正确的识别句柄
我们可以使用文氏图来解释这个情况
所有的上下文无关法作为一个集合,明确的上下文无关语法是他的一个子集
LR(k)语法更小
L代表从左到右扫描,R代表了最右推导,k代表了需要向前看k个数量的token
LR(k) 语法是我们所知道的最普遍的确定性语法之一,实战不用
大部分自下而上型工具实际会用到一种语法,被称为LALR(k)语法
他是LR(k)的子集,然后我们会主要讨论的是它们的一个简化版语法
SLR(k)上下文无关法
解析器会看到这个栈,在每一步中,解析器都会知道有哪些元素在栈内
有一个定义:
假设α是一个可行前缀,如果此处有一个w,并且α|w是移位归约解析的一个有效配置的话,这里的α它处于栈顶,w是input输入的剩余部分
意味着解析器知道α的这部分,但是对w的那部分并不了解
解析器虽然能向前看一些内容,但是也就是一个token,
可行前缀是一个字符串,他不会延伸到句柄的右端
我们称他为可行前缀的理由是因为他是句柄的前缀,因此只要解析器在栈上有可行的前缀的话,就不会检测到解析错误
自下而上解析的第三个也是最后一个重要的事实
对于任何语法来说,可行前缀集就是一个正则语言
这个就是自下而上解析的基于这个事实开发的,可行前缀集可以被有限自动机所识别
example
演示可接受可行性前缀的自动机如何进行计算
辅助的额外定义
定义item
item是指一个产生式右手边某处存在的一个.
例如,我们有一个item这里的. 始终在产生式右手边的左端处,(E)的最左端
我们也有一个. 始终在产生式右手边的右端处(E) 的最右端
我们还会有. 在括号内的情况
在这个例子中,对这个产生式,存在了四种item
有一种特殊情况,对于一个epsilon产生式,在产生式的右手边没有任何符号
我们就会说这里有个item,即X->.
如果你看过帮助页的话,这些item被称为LR(0) items
我们准备讨论如何识别可行前缀
在栈内,我们只有产生式右手边的部分内容
栈内的内容并不是随机的。他有一种特殊的结构,这些片段始终是产生式右手边的内容的前缀
在一个成功的解析中,栈上的元素始终必须是产生式右手边的前缀
在栈内,我们有(E
在input 我们有)
(E就是 T->(E) 的前缀
当我们将剩下的)也压入栈内后,我们就会得到一个产生式右手边的完整内容,这样我们就准备好对他进行归约操作了
这就是item的由来,
这个item就是T->(E.) 用来描述这种情况
他表示了,目前为止,我们已经看到了这个产生式的(E 这部分
并且我们希望在之后看到)
. 的左侧就是栈内的,右侧就是在我们能够进行归约操作前我们想要读取的内容,解析器并不知道输入是什么
我们来讨论栈的结构,这是一个存储了产生式右手边前缀的栈
有一些列前缀堆叠在栈上,如果取处一个前缀,Prefixi 这必须是产生式右手边的前缀
也就是,prefixi最终会被归约为产生式左边的元素,这个例子中最终归约为Xi
然后Xi必须是栈内前缀所缺失的后缀部分
递归的,前缀k上的所有前缀最终都必须归约聚合到前缀k右侧的缺失部分前面,即右手边的α_k
我们始终都在栈的最上层的前缀进行处理,当前缀递归后,就会对栈中更下面的前缀进行处理
输入的字符串是(int*int)
栈内我们有(int* input还剩下int)
我们从下面开始处理的 栈顶是T-》int*T产生式的前缀
读到int*我们想要读T
int下面还有一个前缀,int和(之间 有一个epsilon
也就是说栈内位空,但是,int*归约为T,T归约为E,
现在我们能记录栈内所有的item
在上面的处理中,我们只看到了前缀,就让他处理,变成产生式右侧的一部分
每一次向前移动,都要把做左手边的内容归约到不能不能再归约位置,也就是说,每移动一次,就要再次进行整体的归约操作,即每次栈顶放置的就是归约后的非终结符
问题再于是被一系列产生式右手边的片段
这些产生式右手边的片段内容最终会归约为所缺后缀的前置部分
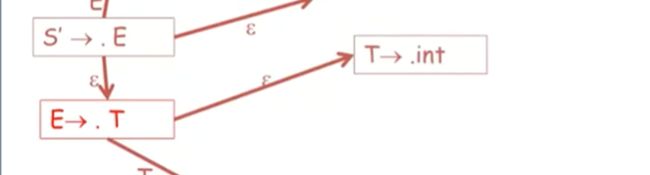
08-03: Recognizing Viable Prefixes (14m57s)【识别可行前缀】
研究一波算法
第一个点,给G语法添加一个伪产生式S’->S
只是为了让我们试着计算出G的可行性前缀而进行的设置
我们声明,对于给定语法的可行前缀集,它是正则的,
也就是需要构建一个非确定性有限自动机(NFA) 来识别可行前缀
NFA读取栈,从底到上,让我们能够知道解析器有没有真的遇见解析错误,yes,没问题,栈中内容能够完全正确的解析这个输入,no遇到了错误,无效输入
第三个点,需要让自动机进行怎样的状态转换
假设我们处于某个状态E->α.Xβ
这个表示,我们目前在栈中读取到了α,自动机是自下而上的读取这个栈
如果这个是一个有效栈的话,如果栈内的下一个元素是X
我们就可以转换到这个状态,E->αX.β
我们现在记录了我们在栈内看到X的这个事实,并且我们之后想看到产生式剩下的部分β,
我们为每个item添加这个转换,如果当有任何符号出现在. 的右边的话,. 就会向右移动
X是任意语法符号,不仅仅是一个非终结符,但是这里的第四条是仅仅针对非终结符
在栈内的这些东西必须是从X推导出来的,我们通过使用一系列的X的产生式能生成这些东西,因为最终会归约为X
如果栈内没有X的话,我们可以进行空跳,移位到某个状态,也就是当我们试着去识别右手边内容的时候,我们可以加上某些从X推导出来的内容
只有两种操作,一种是我们在栈内寻找语法符号,另一种是对产生式右手边前缀进行扩展
当我们在栈内要看更多产生式右手边内容的时候,NFA会试着猜测这些前缀的末尾是什么
如果当前栈上看到的是产生式α,那么接下来这里就必须是X,此处的这一点必须标记在栈中α右手侧,他指向另一个产生式
我们希望可以看到那些从X指向的产生式中所推导出来的一些东西
自动机中的每个状态都是一个接收状态,
这意味着如果自动机成功的处理了整个栈,那么这就是一个可行的栈
要注意就是对于每个可能的符号而言,不是每个状态都会有相应的状态转换(可能该符号就找不到可以适配的产生式)
这就会造成大量的栈被拒绝,自动机会被卡住
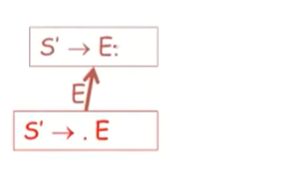
最后一个,自动机的开始状态S' 即item 就是S'->.S
自动机的状态就是语法的item,每一个item都可以认为是一个语法规则
这就是为什么我们添加这个伪产生式的原因,这样能方便我们命名开始状态(也就是对每一个小的语法规则进行命名)
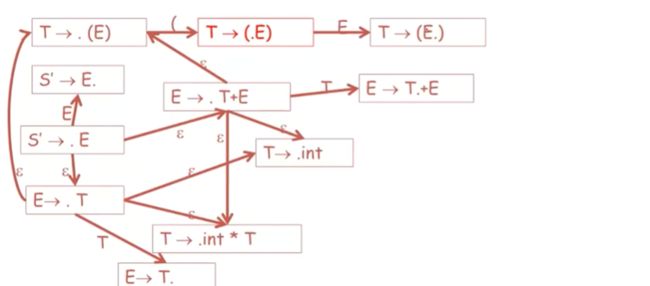
example
我们通过额外的产生式S'->E 来对她进行扩展
这个就是用来识别该语法可行前缀的自动机
我们一步一步推导,
我们首先从自动机开始状态开始,我们读取这个栈,并且希望之后在站内看到一个E
如果没有的话,我们也希望看到某些从E推导出来的东西出现在栈内,
基于这个状态,我们能做什么转换呢?
一种情况,我们在栈内看到了E
. 移动完毕,我们已经在栈内读到了第一个item,或者说在栈内读到了E,
这样我们就已经完整的读取到了这个产生式的右手边内容
也就是,我们可能完成了解析,
但是如果没有在栈内看到这个E的话,那么你就希望你能看到某些由E推导出来的东西在栈内出现,
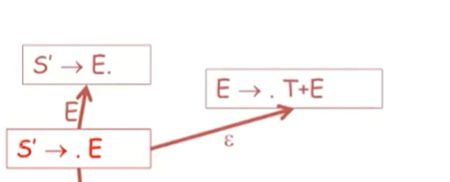
![]()
空跳,一种可能是,自动机最终会用这个产生式E->T
我们还没看到任何东西,所以我们把. 放在左边,以此来表示我们希望看到一个T,这样就能归约成E,然后归约为S’
另一种可能,如果在栈内没有读到T,就是我们可以使用E->T+E
因为我们还没有看到任何T,因此,. 仍然会在左手边
我们不知道哪一个产生式的右手边内容会出现在栈内,这些产生式甚至没有提取左公因子
因此我们并不知道它会去选择使用E->T,还是E->T+E
但是我们只需要使用NFA的预测能力,它可以去选择使用哪个产生式,
NFA接受任何可能的选择,
当然我们能将他编译为一个确定性自动机,这样就不会做任何猜测了
这里我们使用的是非确定性自动机,
一种可能就是,传来的是T,.推进 当. 在最右侧的时候,就可以准备归约了
这就是识别句柄的方式,
当我们最终到达一个状态,即. 在T右侧的时候,这就表示这个可能是一个句柄,看可以用来归约,
如果在栈内没有看见T,我们就看到某些由T所推导出来的,
一种是T-》int
另一种是T-》(E)
第三种是,T-》int*T
当然. 始终在左端,因为没有真的收到任何字符串对吧,
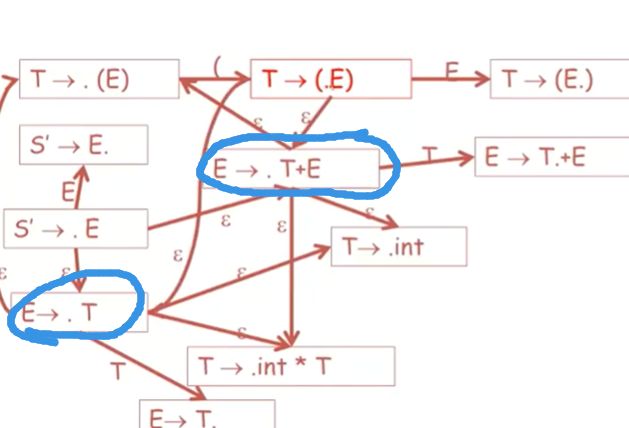
我们切到这个item,E->.T+E
一种可能是看到T了,读取
另一种是遇到某些从T推导出来的
T开始的产生式,
能从E->.T+E 这个item转化到这三种状态
我们目光转向T->.(E)
因为括号是终结符,因此不会有推导出来的东西对吧,
我们必须看到栈内有括号,
因为是E,因此,可以找E或者E生成的一系列
当然我们也想要看到E所推导的
添加了两个状态转换
回顾一下,这里找下一个终结符
最终以T->(E). 这个item结束
我们来看这条路
读取到E,在把E能推导的或者E本身的连一下
把剩下的终结符转换一下
再把T推导的东西补上
这就是用来识别这个语法可行前缀的自动机的所有状态和状态转换了
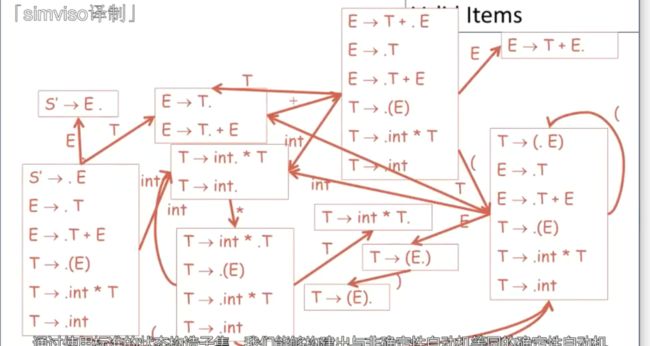
08-04: Valid Items (3m31s)【有效item】
通过构造标准的状态构造子集,能够构建出于非确定新自动机等同的确定性自动机
这个是用来识别完全相同语言的确定性自动机
每个状态都是一个item集合
在每个状态中,都有一组非确定性自动机的状态,
这意味着,非确定性自动机可能处于上述集合中的任何一种状态
这个状态是开始状态,也就是这一整个,因为他有S’->E 这个item
这种确定性自动机状态成为item的各种规范集合或者LR(0) item的规范集合
现在我们需要另一个定义
对于一个可行前缀αβ来讲,我们会说这样一个给定的item:X->β.Y是有效的
如果满足一下条件,则从起始符号开始S‘
通过一系列最右推导,我们能够得到一个配置αXw
进一步得到X->βy
就是说,当解析完α后,在α后紧挨着就看到了β,β在栈上,那这些可以解析到栈顶的items就是有效的items
那这个item可能就是这个非确定性自动机的确定状态,
换一个更加简单的方式来说就是,对于给定的可行前缀α,在DFA读取到这个前缀后,会有一个确切有效的item来辨析辨别,即该item在这个DFA管理的最终状态中,
当你在栈内看到α,这就是用来描述状态的items
对于许多前缀来说,item通常是有效的
![]()
例如,itemT->(.E) 对于一系列的’(‘ 来说是有效的
比如有五个括号,
就会在这里item,进行五次循环,
08-05: SLR Parsing (14m16s)【SLR解析】
SLR解析(简单LR解析) 是基于有效item和可行前缀的思想构建的
LR(0)解析假定
我们有一个栈,栈内包含元素α,并且下一个输入是词法单元t,这个DFA能用来识别可行前缀,输入α,状态s结束
如果DFA的最终状态S包含了x->β,这个item的话,也就是栈顶我们看到了产生式右手边的完整内容,也就是X->β
此外,在堆栈下方的所有内容适用于这个状态中的x->β.,也就是说x->β.也是一个有效item
可以使用X->β 来归约
移位:
某种状态s,包含X->β.tw
那么LR(0)在解析上会遇到什么问题呢?
他可能会遇到两种问题
如果DFA中的任何一种状态里有两个可能的归约操作的话,这意味着,这回又两个完整的产生式可供选择进行归约操作
然后还没有足够的信息供我们去选择该执行哪个归约,所以这部分并不是完全确定性的
没有足够的信息供我们选择去执行哪个归约,所以这个部分并不是完全确定性的
被叫做reduce/reduce冲突:如果一个特定状态有两个item,即可以进行两个归约的话,那么这种冲突就会发生
另一种就是,在DFA的最终状态中,当解析器读取了栈内内容后,可能会遇到一个item可以进行归约操作,但是另一个item进行移位操作
这就被成为shift/reduce冲突
这个例子中,这个状态只有一个冲突,即当t是输入中的下一项时,不知道
t移入栈内,还是选择归约,
这个是前两集识别可行前缀的DFA
这个DFA中存在了一些问题,
当我们读取到+号,我们既可以归约E->T,也可以读取E
会有一个shift/reduce冲突,
当然这个状态,我们也存在shift/reduce冲突,
改进LR(0) 就是通过SLR
在移位或则和归约的时候加入一些引导,提升LR(0) 的解析
我们只是给这个归约例子添加了一个新的条件,
这个状态是,β在栈顶,可以进行归约,
这里的自动机并没有利用输入中出现的任何优势(即根据后续输入来判断接下来所用的产生式)
这里所做的选择完全是基于栈的内容
我们预估后面的,既然后面会压入栈内,也就是说后面的t是属于Follow(t)的
如果t不能跟在X后面的话,或者说t是一个终结符,那么他就不能跟在非终结符X后面,(tips:此时是X->β.,如果后面跟着一个终结符,β后面的点就没有必要)
所以新加限制t∈Follow(X)
![]()
如果在这些规则下还存在冲突的话,这个语法就不叫SLR
这些规则就构成了用于检测句柄的启发式规则,
当我们处于栈顶的时候, DFA 就会告诉我们可能有哪些item,以及输入中接下来会出现的内容
通过这个来定义我们的归约选择,这个可以精确引导,
我们改进这个旧的例子
在这两个冲突的时候,
读取到+ 移位,或者我们可以进行归约,,
也就是在输入是Folllow(E)中的元素时,我们才会去进行归约,
我们之前算过, Follow(E)={$,)}
因为)紧跟在E后所以在里面
只有读取到这些,才会归约,
我们来看另一个例子的FollowT
FollowT包含了FollowE的所有元素,但同时,+号也是followT的元素,因为他在T的后面用到了
当我们处理完输入,或者下一个元素是)或者+的时候,我们进行归约,
整个这个就相当于是一个SLR(1)语法
许多语法都不是一个SLR语法,SLR只是对LR(0)的改进,它依然不是一类非常常见的语法
例如:所有语义混淆的语法都不是SLR语法
我们可以通过优先级声明来让解析器更加语法化,并解决冲突。
我们回到这个最自然,同时语义也是最混淆的语法,即在整数运算时用到+和*
当我们为该语法的可行前缀构造DFA的时候,
一个状态中,会有两个item,冲突,当我们栈内有E的时候,下一个的接受会影响,*和+ 是要规约呢还是要移位呢?
是否*和+有优先级的区别
通过声明,*号比+有更高的优先级,就不会有冲突
声明并不是去定义优先级,他们会告诉我们请做这个操作,而不是另一个操作,
这里给出了SLR解析的相关算法
M是解析自动机,用来识别前缀,初始时,|在最左边,表示栈空,
$来标记输入的末尾
我们会进行重复操作,直到栈内,只有开始符号并且输入中只有$ 这意味着完成了所有的输入,也将整个的输入归约为了开始符号,
我们当前是α|w α是栈内内容,w是输入中剩下的部分
我们去运行自动机,让他读取栈内α,(我们需要使用自动机对栈进行一波前缀解析操作,为后续做准备,)如果M拒绝了α的话,或者如果M表示α并不是一个可行前缀的话,那么我们就会爆出一个解析错误
M如果接受了α,如果以这个状态下item结束的话,就会去看下一个输入a
我们就会进行移位操作,如果下一个看到终结符a,这是ok的,
我们进行归约,要求和我们之前的一样,
而事实上,这里并不需要M检查前缀,因为不符合的,都会被爆解析错误,(在最后)
如果在最后一步有任何冲突的话, 就不是SLR(k)语法
k就是向前看几个token,一般向前看一个
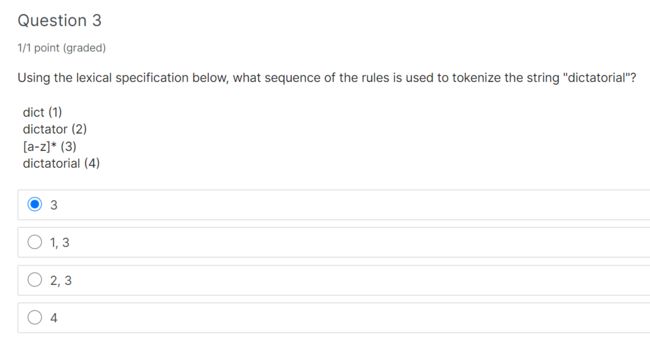
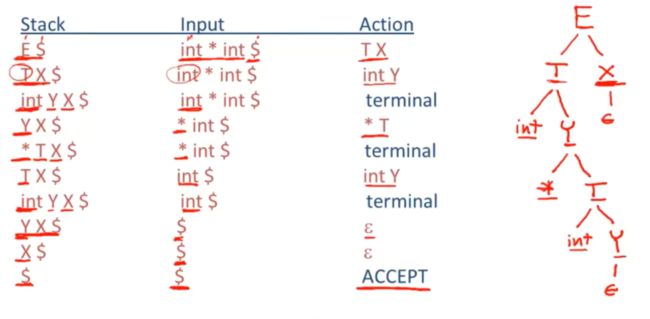
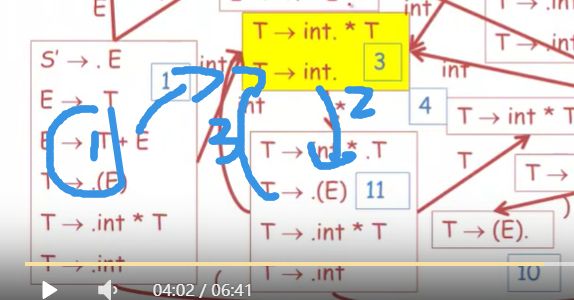
08-06: SLR Parsing Example (6m42s)【SLR解析案例】
简单回顾:
$标记结尾,
状态一开始,栈为空栈,对于初始状态,这些产生式是可以进入的
这些item中,有两个item可以让我们将int进行移位操作,
这里点都在最左边,没办法归约
在初始状态下,DFA会在状态1停止,这个状态让我们移位
进入下一个状态,下一个元素是*
当然首先我们可以通过T-》int. 来进行归约,只有当接下来输入元素是FollowT,才能进行归约,
但是,*不是FollowT的元素,因此不能使用来归约,
我们可以看另一个item,可以将*进行移位操作
下一个输入元素是int,
栈内有int和*
*处于栈顶,下面是int,DFA从栈底开始读取
int -》*》然后进入11状态
我们看到没有归约,点没有在最右边,因此可以是移位
下一个int 移位,
栈内为int*int
最后到了第三个item 下一个输入是$
因此是FollowT的元素,因此可以进行归约
然后我们再接着读取栈内,int * T
读取到T,到达了4,在状态4停止。
可以进行归约,
栈内读取到T,从1跳到了5
如果输入中的下一个元素是+好,就能进行移位,可惜不能,
因此使用E-》T 进行归约,
栈内只剩E,
因此,我们只有一个状态可以,然后我们接受这个解析
0 8-07: SLR Improvements (11m49s)【SLR改进】
SLR解析算法 比较低效
自动机读取栈时所做的大部分工作,实际上是多余的
每次重复的去读取栈,就会十分的耗费时间空间
我们只需要记住栈前缀是多少即可省略这些重复的步骤
栈内都存储的是一个pair,
这里的DFA状态就是DFA的运行结果,
sym1----symn就是之前的栈内保存的符号,与dfa一一对应
在栈上任意取一点,就会得到DFA对整个栈中这一点前的内容的运行结果
我们需要将开始状态存储在栈底,
算法细节:
首先定义一个goto表, 根据一个状态和一个符号映射到另一个状态
goto表仅仅是一个DFA的状态转换函数,是把DFA的图以数组的形式写出
我们的SLR算法有四种操作,
移位 会压栈
x代表DFA的一个状态
pair的另一个元素a就是当前输入
归约 会从栈内弹出
最后成功解析没有成功解析的,error,
接着是一个解析表,也就是动作表,他告诉我们在每个可能的状态下,我们应该进行哪一种操作,
动作表是根据自动机的一个状态和下一个输入符号来做的索引
里面有移位,归约,accept,error
如果在栈顶处自动机的最终状态中有一个item,也就是说可以对a进行移位操作,输入a,可以进入状态j
当我处于状态i并接受到输入a,就会将j压入栈内
![]()
也就是状态i结束,并且下一个输入a的时候,pair
其他几个同理,
处于状态si,并且输入为a,使用产生式X->α进行归约
如果左手边符号是特殊开始符号S‘的话,我们不进行归约,
如果要归约的item是S’->S. 此时处于输入末尾,那就接受accept
其他情况报错error
这个就是SLR原始算法
初始输入I,index变量j,可以指向token
repeat 重复这些过程直到我们成功解析
他没有用到栈内的任何东西,只是使用了DFA的状态和输入,
在编译器的后续阶段,我们仍然需要用到程序,用来类型检查和代码生成
被广泛使用的自下而上型解析算法是基于一类被称为LR语法的更强大的语法
LR语法和SLR本质区别就是把向前看这种能力内置到了item中,
LR(1) item 就会变成一个包含 一个item的pair
如果看到$,当然就是进行归约,
现在一般使用LALR 他是对LR的一种优化
08-08: SLR Examples (12m47s)【SLR案例】
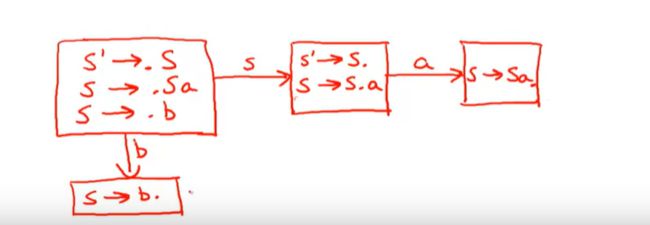
提供了一些语法,
S->Sa
S->b
我们先写出解析该语法所对应的自动机
首先补充一个开始状态,S'->S
S'->S
S->Sa
S->b
S'->.S 这个item就是这个NFA解析自动机的开始状态
我们继续前进,然后算DFA的第一个状态重,必须要有那些item
NFA中的所有空跳, 只有在我们在栈上看不到一个非终结符的时候才会产生,这往往可以从对非终结符元素推导的过程中看到,(比如这里的First集,这里包含了通过空跳得到的元素)
在NFA中,对于该非终结符的所有产生式而言,内在的first集都有一个空跳epsilon
空跳得到,S->.Sa
对于S而言,也可以,S->.b
这三个item就是DFA第一个状态所包含的items
现在我们需要思考下,我们可能在栈上看到的每个符号下可能发生的状态转换
如果我们在栈内看到一个b,状态只有S->b.
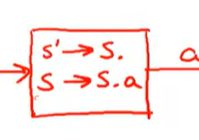
另一种可能性,看到S
一种是S'->S., 另一个S->S.a
这些大部分状态不存在归约/移位 冲突
如果说判断是否是SLR(1),
但是有一个
读取到S,既可以归约,又可以移位
S’的Follow集合有什么呢?
也就是S’ 后面能跟什么呢?也就是唯一的$
example
一个比较复杂的例子
初始语法,
我们接着构建解析自动机
正常需要我们去画NFA的草图,然后进行状态子集的构建,
因为语法规则比较少,这里直接写,.后跟S我们可以空跳
S'->.S
S ->.SaS
S->.b
这就是关于S的初始item
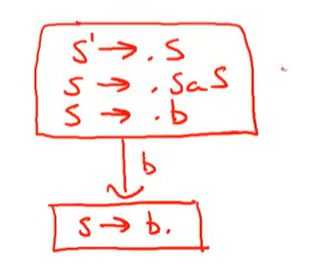
可以在栈内看到一个b
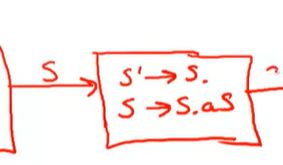
另一种,栈内看到S,
看到a,
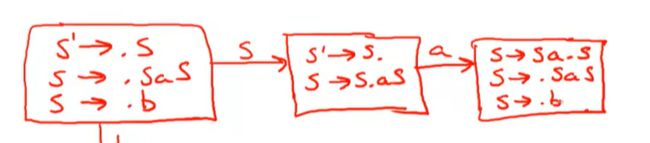
这里就会复杂一些,因为.S我们在栈内除了会看到一个S,我们也可能会在栈内的下一个位置看到某些从S推导出来的东西,
也就需要把S的产生式都填进来
如果看到b,就转到b,看到S就会产生新的状态
我们有一次遇到a的时候,
就会回去,
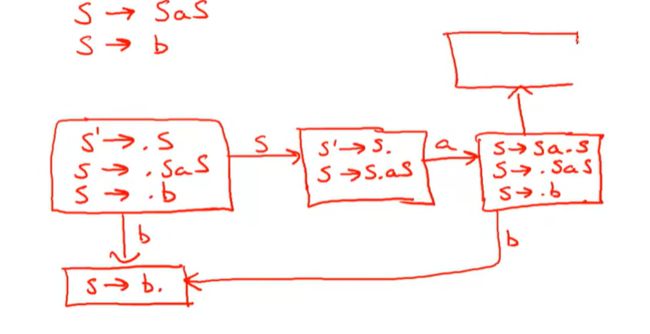
这就是完整的状态转化那系统,也就是DFA的所有状态,
这是一个SLR(1)么?
我们需要检查一下reduce/reduce,shift/reduce冲突
首先找到这里,
Follow(S’)={$}
这儿不存在冲突,
我们看这里
只有栈内的下一个元素为b或者s的时候,才会发生状态转换
没有归约,
![]()
最后一个状态
第一个item就是可以进行归约的item
FollowS中的任何都应该使用S->SaS来归约,根据S’->S,FollowS’都是followS的元素
Follow(S) = {$,a,}
根据S->SaS 第一个S后面跟着a,所以followS里面有a
又根据,S是最右边的一个,因此产生式右手边的任何东西也就是左手边非终结符Follow集合中的元素,FollowS是FollowS的子集,
在输入中,遇到$进行归约,遇到a移位,这里会有shift-reduce冲突
这并不是一个SLR(1)语法