【刷题之路Ⅱ】迷宫问题升级版——找最短路径

一、题目描述

原题连接： 地下迷宫
题目描述：

小青蛙有一天不小心落入了一个地下迷宫,小青蛙希望用自己仅剩的体力值P跳出这个地下迷宫。为了让问题简单,假设这是一个n*m的格子迷宫,迷宫每个位置为0或者1,0代表这个位置有障碍物,小青蛙达到不了这个位置;1代表小青蛙可以达到的位置。小青蛙初始在(0,0)位置,地下迷宫的出口在(0,m-1)(保证这两个位置都是1,并且保证一定有起点到终点可达的路径),小青蛙在迷宫中水平移动一个单位距离需要消耗1点体力值,向上爬一个单位距离需要消耗3个单位的体力值,向下移动不消耗体力值,当小青蛙的体力值等于0的时候还没有到达出口,小青蛙将无法逃离迷宫。现在需要你帮助小青蛙计算出能否用仅剩的体力值跳出迷宫(即达到(0,m-1)位置)。

输入描述:
输入包括n+1行:
第一行为三个整数n,m(3 <= m,n <= 10),P(1 <= P <= 100)
接下来的n行:
每行m个0或者1,以空格分隔

输出描述:
如果能逃离迷宫,则输出一行体力消耗最小的路径,输出格式见样例所示;如果不能逃离迷宫,则输出"Can not escape!"。 测试数据保证答案唯一

示例1
输入
4 4 10 1 0 0 1 1 1 0 1 0 1 1 1 0 0 1 1
输出
[0,0],[1,0],[1,1],[2,1],[2,2],[2,3],[1,3],[0,3]

二、解题

其实这题和上一题[迷宫问题]的主要区别就在于增加了存在多条路径和体力值的设定。所以我们主要的代码就可以直接复用上一题代码，然后再将这些设定补全即可。

1、方法1——暴力递归+更新栈

1.1、思路分析

如上所述，我们主要要解决的就是两个问题：体力值和找到最短路径。
先来看看比较简单的体力问题：
对于体力值的解决方法是比较简单的，因为是要移动才要消耗体力值，所以对于体力值的处理当然是放在找通路函数GetPath里，我们只需要在对应的方向处理对应的体力消耗即可。
**有的朋友可能会这么想：**那我可以传一个体力值的指针进GetPath函数，然后在走向对应的方向时通过指针来对外部的体力值进行加减，而如果需要回溯的话再将体力值加回来啊。
其实没必要这样，而且每次都传入一个体力值的指针变量也怪麻烦的。
我们其实可以灵活地运用递归算法的“回归性”,然后只用局部变量的体力值就解决这个问题。我们知道递归其实是层层调用的关系，在某一次调用结束时也并不是直接返回到最外层而是返回到上一层调用处。
所以我们将体力值设置成局部变量，在递归返回的时候，这个临时变量也不会发生改变，也就相当于恢复了原有的体力值了。
所以我们最终四个方向的递归就可以如下面这样设计：

pos next = { 0, 0 };

    next = cur;
    // 上
    next.row += 1;
    if (isPass(path, row, col, next)) {
        GetPath(path, row, col, next, power - 3);
    }

    next = cur;
    // 下
    next.row -= 1;
    if (isPass(path, row, col, next)) {
        GetPath(path, row, col, next, power);
    }

    next = cur;
    // 左
    next.col -= 1;
    if (isPass(path, row, col, next)) {
        GetPath(path, row, col, next, power - 1);
    }

    next = cur;
    // 右
    next.col += 1;
    if (isPass(path, row, col, next)) {
        GetPath(path, row, col, next, power - 1);
    }

直接通过形参的方式来控制，其实也和局部变量差不多的。

然后就是比较复杂一点的最短路径的处理：
因为我们并不能知道具体那一次找到的通路是最短路径，所以很明显仅使用一个栈是完成不了任务的。我们还需要额外创建一个栈minPathStack来保存当前找到的最短路径，如果后面在找到了更短的路径，就更新minPathStack中的路径。
而在具体的递归中，因为我们现在是可能存在多条路径可走，所以即使在某个方向的递归中已经找到了通路我们还是得继续递归其他的方向，以找到更优的通路，所以我们就要将GetPath函数设置成不带返回值的：正如上面的代码所示的：

最后还有一点需要注意的是： 也是因为可能存在多条通路，所以我们在某一条路上头不通或者体力消耗尽了。当我们往回返的时候还需要将这些走过的坐标再改成可通行的坐标，就如下面的这个用红圈圈起来的坐标：

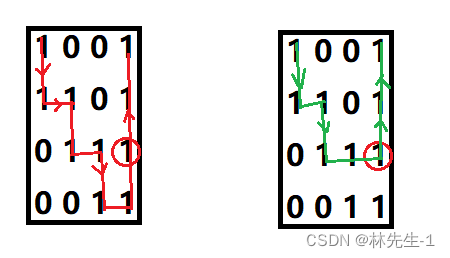
我们发现红色和绿色的两条路都经过了这个坐标，而红色的那条是走不通的(体能不够)，而如果我们在红色的那条路上往回返的时候没有吧走过的坐标再改成可通行的坐标，那到后面在走绿色那条路的时候就没法在通过红圈圈的这个坐标了，那我们也就找不到可行的通路了。

好了，这就是这些就是这一题的重点思路了，剩下的就是代码实现了。

1.2、先将栈实现以下

C选手的第一步当然是自己造轮子啦：

// 定义一个坐标结构体
typedef struct position {
    int row;
    int col;
} pos;
// 先要将栈实现一下
// 重定义数据类型
typedef pos DataType;

// 定义栈结构
typedef struct stack {
    DataType* data;
    int top;
    int capacity;
} Stack;

// 栈的初始化
void StackInit(Stack* ps);

// 压栈
void StackPush(Stack* ps, DataType x);
// 弹栈
void StackPop(Stack* ps);
// 返回栈顶数据
DataType StackTop(Stack* ps);
// 返回栈的数据个数
int StackSize(Stack* ps);
// 判断栈是否为空
bool StackEmpty(Stack* ps);
// 栈的销毁
void DestroyStack(Stack* ps);

// 栈的初始化
void StackInit(Stack* ps) {
    assert(ps);
    ps->data = NULL;
    ps->top = 0;
    ps->capacity = 0;
}

// 压栈
void StackPush(Stack* ps, DataType x) {
    assert(ps);
    // 检查是否需要增容
    if (ps->top == ps->capacity) {
        int newCapacity = ps->capacity == 0 ? 10 : ps->capacity * 2;
        DataType* temp = (DataType*)realloc(ps->data, newCapacity * sizeof(DataType));
        if (NULL == temp) {
            perror("ralloc fail!\n");
            exit(-1);
        }
        ps->data = temp;
        ps->capacity = newCapacity;
    }
    ps->data[ps->top] = x;
    ps->top++;
}

// 弹栈
void StackPop(Stack* ps) {
    assert(ps);
    assert(ps->top > 0);
    ps->top--;
}

// 返回栈顶数据
DataType StackTop(Stack* ps) {
    assert(ps);
    assert(!StackEmpty(ps));
    return ps->data[ps->top - 1];
}

// 返回栈的数据个数
int StackSize(Stack* ps) {
    assert(ps);
    assert(ps->top >= 0);
    return ps->top;
}

// 判断栈是否为空
bool StackEmpty(Stack* ps) {
    assert(ps);
    return ps->top == 0;
}

// 栈的销毁
void DestroyStack(Stack* ps) {
    assert(ps);
    free(ps->data);
    ps->data = NULL;
    ps->top = 0;
    ps->capacity = 0;
}

1.3、代码实现

main函数：
main函数当中我们其实只需要改一下输入的数据增加一个体能值即可，其他的都是调用其他的函数解决。

int main() {
    int Row = 0;
    int Col = 0;
    int power = 0;
    while (scanf("%d %d %d", &Row, &Col, &power) != EOF) {
        int** path = (int**)malloc(Row * sizeof(int*));
        if (NULL == path) {
            perror("malloc fail!\n");
            exit(-1);
        }
        int i = 0;
        for (i = 0; i < Row; i++) {
            path[i] = (int*)malloc(Col * sizeof(int));
            if (NULL == path[i]) {
                perror("malloc fail!\n");
                exit(-1);
            }
        }
        int j = 0;
        for (i = 0; i < Row; i++) {
            for (j = 0; j < Col; j++) {
                scanf("%d", &path[i][j]);
            }
        }
        pos entry = { 0, 0 };
        GetPath(path, Row, Col, entry, power);
        if (!StackEmpty(&minPathStack)) {
            printPath();
        }
        else {
            printf("Can not escape!\n");
        }
    }
    DestroyStack(&pathStack);
    DestroyStack(&minPathStack);
}

GetPath函数：

void GetPath(int** path, int row, int col, pos cur, int power) {
    assert(path);
    StackPush(&pathStack, cur);
    if (cur.row == 0 && cur.col == col - 1) {
        if ((power >= 0 && StackEmpty(&minPathStack)) ||
            (power >= 0 && StackSize(&pathStack) < StackSize(&minPathStack))) {
            // 先销毁原来的minPathStack
            DestroyStack(&minPathStack);

            StackInit(&minPathStack);
            // 将pathStack中的数据拷贝到minPathStack
            int i = 0;
            for (i = 0; i < StackSize(&pathStack); i++) {
                StackPush(&minPathStack, pathStack.data[i]);
            }
        }
    }
    path[cur.row][cur.col] = 2;

    // 判断当前坐标的上下左右四个方向是否能走

    pos next = { 0, 0 };

    next = cur;
    // 上
    next.row += 1;
    if (isPass(path, row, col, next)) {
        GetPath(path, row, col, next, power - 3);
    }

    next = cur;
    // 下
    next.row -= 1;
    if (isPass(path, row, col, next)) {
        GetPath(path, row, col, next, power);
    }

    next = cur;
    // 左
    next.col -= 1;
    if (isPass(path, row, col, next)) {
        GetPath(path, row, col, next, power - 1);
    }

    next = cur;
    // 右
    next.col += 1;
    if (isPass(path, row, col, next)) {
        GetPath(path, row, col, next, power - 1);
    }
    // 将坐标再次改成可通行坐标
    path[cur.row][cur.col] = 1;
    StackPop(&pathStack);
}

判断坐标是否可行：

bool isPass(int** path, int row, int col, pos cur) {
    assert(path);
    if ((cur.row >= 0 && cur.row < row)
        && (cur.col >= 0 && cur.col < col)
        && path[cur.row][cur.col] == 1) {
        return true;
    }
    return false;
}

打印通路：
打印通路我们只需要将打印的栈改成minPathStack再更改一下打印的格式即可：

void printPath() {
    Stack RPathStack;
    StackInit(&RPathStack);

    // 将PathStack栈中的数据全都压入RPathStack栈中
    while (!StackEmpty(&minPathStack)) {
        StackPush(&RPathStack, StackTop(&minPathStack));
        StackPop(&minPathStack);
    }

    pos cur = { 0, 0 };
    // 再将RPathStack栈中的数据取出来打印
    while (!StackEmpty(&RPathStack)) {
        cur = StackTop(&RPathStack);
        StackPop(&RPathStack);
        printf("[%d,%d]", cur.row, cur.col);
        if (!StackEmpty(&RPathStack)) {
            printf(",");
        }
    }
    DestroyStack(&RPathStack);
}

其实这一题的难度已经到达了中等偏上的难度，这种难度的题对你的代码练习量和代码的控制能力是有很高的要求的，里面的各种细节和问题也并非是一篇简单的题解能够说清楚的。
所以最好的建议还是自己动手多刷几遍(当然我不建议大家用C语言来刷……)。