leetcode - 矩阵区域和

1314. 矩阵区域和 - 力扣（LeetCode）

给你一个 m x n 的矩阵 mat 和一个整数 k ，请你返回一个矩阵 answer ，其中每个 answer[i][j] 是所有满足下述条件的元素 mat[r][c] 的和： 

• i - k <= r <= i + k,
• j - k <= c <= j + k 且
• (r, c) 在矩阵内。

示例 1：

输入：mat = [[1,2,3],[4,5,6],[7,8,9]], k = 1
输出：[[12,21,16],[27,45,33],[24,39,28]]
示例 2：

输入：mat = [[1,2,3],[4,5,6],[7,8,9]], k = 2
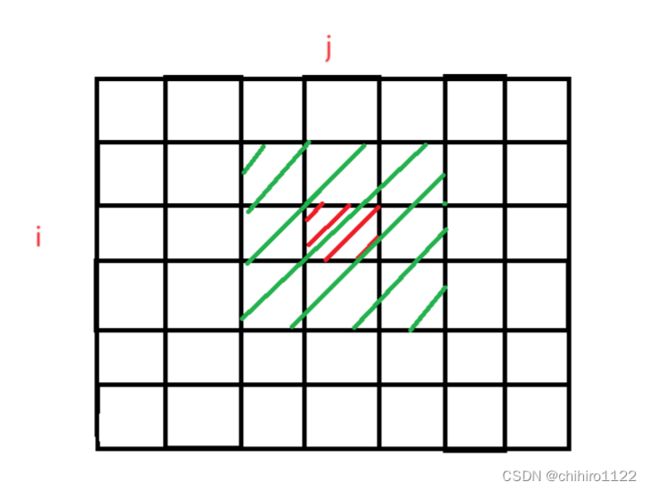
输出：[[45,45,45],[45,45,45],[45,45,45]]

题意就是要计算 假设给出的 mat[i][j] ，那么就要是要计算下图当中给出的 区域的全部元素之和：
 

新返回的矩形当中，应该存储的是上述 绿色区域当中的全部的 元素之和。（k = 1）

 所以，我们可以利用二位矩阵的前缀和 来解决上述的问题。

对于 前缀和 二位矩阵 的计算，可以参考之前博客：

leedcode 刷题 - 除自身以外数组的乘积 - 和为 K 的子数组-CSDN博客

leetcode - 串联所有单词的子串 - 最小覆盖子串 - x 的平方根-CSDN博客

 上述就是递归公式，但是 dp[x2][y2] 不是在 dp 这个 二维前缀和数组当中的，这个位置是没有 数据的，所以，其实这个位置的数据是在 mat 当中的。也就对应的是 mat[i][j] 。

所以，上述就计算出了存储前缀和的二维数组。

此时，我们只需要根据上述的 存储前缀和的二维数组，就可以像下图当中这样去 计算，某一个满足题意的 区间的 元素之和：
 

 即：

ret = dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1]

 上述就是递推公式。

 在上述计算出递推公式之后，就可以开始计算上述的 x1  y1 和 x2  y2 了。

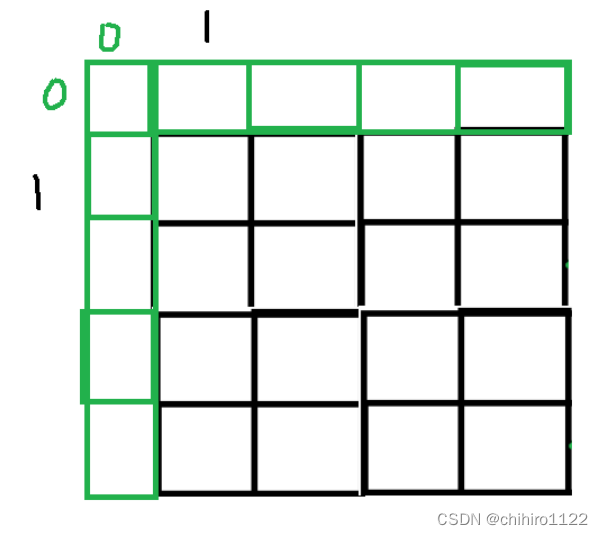
 上述前缀和二维数组当中的 下标是从 (1, 1) 开始计数的，但是，在题目当中的二维数组是从 (0,0) 开始计数的，所以，为了方便上述 前缀和二维数组的计算，所以，我们直接把 dp 数组加一行加一列：

使用黑色位置存储元素值。

dp[x][y] -> mat[x - 1][y -1]

dp[x][y] -> ans[x - 1][y -1]

所以此时应该是：

完整代码：
 

class Solution {
public:
    vector> matrixBlockSum(vector>& mat, int k) {
        int m = mat.size(), n = mat[0].size();

        //计算出前缀和二维数组
        vector> dp(m + 1, vector(n + 1));
        for(int i = 1;i <= m;i++)
            for(int j = 1;j <= n;j++)
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + mat[i - 1][j - 1];

        // 计算出 answer 二维数组的值
        vector> ret(m, vector(n));
        for(int i = 0;i < m;i++)
            for(int j = 0;j < n;j++)
            {
                int x1 = max(0 , i - k) + 1, y1 = max(0 , j - k) + 1;
                int x2 = min(m - 1 , i + k) + 1, y2 = min(n - 1 , j + k) + 1;
                ret[i][j] = dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1];
            }
        return ret;
    }
};