字符串冲刺题

关卡名	字符串冲刺题	我会了✔️
内容	1.掌握最长公共前缀问题	✔️
	2.掌握字符串压缩问题	✔️
	3.如果想挑战一下就研究：表示数值的字符串	✔️

1 最长公共前缀 

这是一道经典的字符串问题，LeetCode14 先看题目要求：编写一个函数来查找字符串数组中的最长公共前缀。如果不存在公共前缀，返回空字符串 ""。

示例1：

输入：strs = ["flower","flow","flight"]

输出："fl"

示例2：

输入：strs = ["dog","racecar","car"]

输出：""

解释：输入不存在公共前缀。

要解答这个问题，我们需要先看一下公共前缀的分布有什么特点，如下图：

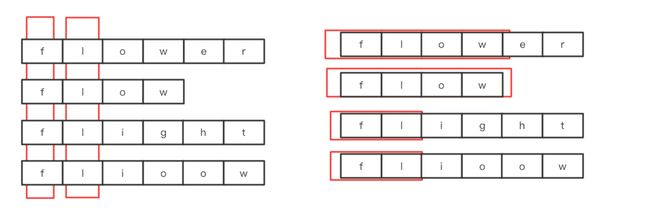可以看到，第一种方式，我们可以竖着比较，如左图所示，每前进一个位置就比较各个串，看是不是都是相等的，只要在某一轮遇到一个不相等的，那么就结束。
第二种方式，还可以横着比较，先比较前两个找到公共前缀fix1，然后再和第三个比较公共前缀得到fix2，我们可以确定fix2一定不会比fix1更长，然后和第四个比较，得到fix4，一直到最后一个fixn。每次得到的fix都不会比前面的长，最后比较完了还剩下的就是需要找的前缀了。
看到这里你是否有种似曾相识的感觉，我们前面合并K个数组或者K个链表不也是类似的思路吗？是的，就是类似的思路。
第三种方式， 我们是否可以对第二种进行优化一下，借鉴归并的思想，先两两一组找fix，然后将找到的fix再两两归并呢？当然可以了，这就是归并的方式。
先看第一种的实现方法，竖着比较。纵向扫描时，从前往后遍历所有字符串的每一列，比较相同列上的字符是否相同，如果相同则继续对下一列进行比较，如果不相同则当前列不再属于公共前缀，当前列之前的部分为最长公共前缀。

public String longestCommonPrefix(String[] strs) {
        if (strs == null || strs.length == 0) {
            return "";
        }
        int length = strs[0].length();
        int count = strs.length;
        for (int i = 0; i < length; i++) {
            char c = strs[0].charAt(i);
            for (int j = 1; j < count; j++) {
                if (i == strs[j].length() || strs[j].charAt(i) != c) {
                    return strs[0].substring(0, i);
                }
            }
        }
        return strs[0];
}

第二种是横着依次比较，依次遍历字符串数组中的每个字符串，对于每个遍历到的字符串，更新最长公共前缀（其实就是看是否要缩短，一定不会变长），当遍历完所有的字符串以后，即可得到字符串数组中的最长公共前缀。如果在尚未遍历完所有的字符串时，最长公共前缀已经是空串，则最长公共前缀一定是空串，因此不需要继续遍历剩下的字符串，直接返回空串即可。

public String longestCommonPrefix(String[] strs) {
    if (strs == null || strs.length == 0) {
        return "";
    }
    String prefix = strs[0];
    int count = strs.length;
    for(int i=1;i

 2 字符串压缩问题

这个题也是出现频率很高的题目，经常在面经中看到。实现起来略有难度，我们一起看一下。
LeetCode443 给你一个字符数组 chars ，请使用下述算法压缩：
从一个空字符串 s 开始。对于 chars 中的每组 连续重复字符 ：

• 如果这一组长度为 1 ，则将字符追加到 s 中。
• 否则，需要向 s 追加字符，后跟这一组的长度。压缩后得到的字符串 s 不应该直接返回 ，需要转储到字符数组 chars 中。需要注意的是，如果组长度为 10 或 10 以上，则在 chars 数组中会被拆分为多个字符。

请在 修改完输入数组后 ，返回该数组的新长度。你必须设计并实现一个只使用常量额外空间的算法来解决此问题。

示例1：

输入：chars = ["a","a","b","b","c","c","c"]

输出：返回 6 ，输入数组的前 6 个字符应该是：["a","2","b","2","c","3"]

解释：

"aa" 被 "a2" 替代。"bb" 被 "b2" 替代。"ccc" 被 "c3" 替代。

示例2：

输入：chars = ["a"]

输出：返回 1 ，输入数组的前 1 个字符应该是：["a"]

解释：

没有任何字符串被替代。

示例3：

输入：chars = ["a","b","b","b","b","b","b","b","b","b","b","b","b"]

输出：返回 4 ，输入数组的前 4 个字符应该是：["a","b","1","2"]。

解释：

由于字符 "a" 不重复，所以不会被压缩。"bbbbbbbbbbbb" 被 “b12” 替代。

注意每个数字在数组中都有它自己的位置。

这个题貌似采用双指针策略来处理就行，但是再分析发现三个指针才够。
我们可以使用两个指针分别标志我们在字符串中读和写的位置，还要一个指针left用来标记重复字段的开始位置。read指针不断向前读取，每次当读指针 read 移动到某一段连续相同子串的最右侧，我们就在写指针 write 处依次写入该子串对应的字符和子串长度即可。
当读指针read 位于字符串的末尾，或读指针read 指向的字符不同于下一个字符时，我们就认为读指针read 位于某一段连续相同子串的最右侧。该子串对应的字符即为读指针 read 指向的字符串。我们使用变量 left 记录该子串的最左侧的位置，这样子串长度即为 read−left+1。
这里还有一个问题，就是长度可能超过10，因此还要实现将数字转化为字符串写入到原字符串的功能。这里我们采用短除法将子串长度倒序写入原字符串中，然后再将其反转即可。

public int compress(char[] chars) {
        int n = chars.length;
        int write = 0, left = 0;
        for (int read = 0; read < n; read++) {
            if (read == n - 1 || chars[read] != chars[read + 1]) {
                chars[write++] = chars[read];
                int num = read - left + 1;
                if (num > 1) {
                    int anchor = write;
                    while (num > 0) {
                        chars[write++] = (char) (num % 10 + '0');
                        num /= 10;
                    }
                    reverse(chars, anchor, write - 1);
                }
                left = read + 1;
            }
        }
        return write;
    }

    public void reverse(char[] chars, int left, int right) {
        while (left < right) {
            char temp = chars[left];
            chars[left] = chars[right];
            chars[right] = temp;
            left++;
            right--;
        }
    }
}