JavaSE语法之四：方法的使用（超全！！！）

一、方法的概念和使用

1. 方法的概述

在编程中，我们可以将频繁使用的代码封装成“方法”，需要的时候直接拿来用即可，避免了一遍一遍的累赘。

2. 方法的定义

语法格式：

public static 返回值 方法名(形式参数类型 形参){
//方法体
}

【注意】

1. 返回值类型：如果方法有返回值，返回值类型必须要与返回的实体类型一致，如果没有返回值，必须写成void
2. 方法名字：采用小驼峰命名
3. 参数列表：如果方法没有参数，()中什么都不写，如果有参数，需指定参数类型，多个参数之间使用逗号隔开
4. 方法体：方法内部要执行的语句
5. 在java当中，方法必须写在类当中
6. 在java当中，方法不能嵌套定义
7. 在java当中，没有方法声明一说

3.方法的调用

调用方法是在 main 方法中进行调用的，分以下两种情况：

1. 当方法有返回值时

参数类型 参数名 = 方法名(实参)；
如：
boolean flg = isLeapYear(2000);
此时：①等号后面 括号内传参 ②等号前面boolean flg 接收返回值 ①和②两者一样都不能少

2. 当方法没有返回值时

方法名(实参);
如：
sum(1,2);

实例： 判断是否为闰年

	//定义方法
	public static boolean isLeapYear(int year){
		if((0 == year % 4 && 0 != year % 100) || 0 == year % 400){
			return true;
		}else{
			return false;
	}
}
	public static void main(String[] args){
	//调用方法
		boolean flg = isLeapYear(2000); 
		 System.out.println(flg);
}

方法定义到调用的全过程：

调用方法—>传递参数—>找到方法地址—>执行被掉方法体—>被调方法结束返回—>回到主调方法继续往下执行

1. 定义方法：返回值是什么类型？方法名叫什么？形参有几个？形参是什么类型？形参什么顺序？
2. 调用方法：方法名()——看看有几个参数？都是什么类型？什么顺序？
3. 方法有返回值吗？要不要接收？拿什么类型接收？接收了返回值，我用返回值干什么？

其中：

• 方法的调用是在一块内存当中，这块内存叫栈；
• 当方法遇到return或者遇到右花括号代表当前方法结束了，对应方法开辟的栈帧回收了。

4. 实参和形参的关系（重要）

我们目前看到的，实参和形参都是按照值传递。
形参只是方法在定义时需要借助的一个变量，用来保存方法在调用时传递归来的值。

【实例】

		public static int getSum(int N){ // N是形参
			return (1+N)*N / 2;
	}
		public static void main(String[] args){
			getSum(10); // 10是实参,在方法调用时，形参N用来保存10
			getSum(100); // 100是实参，在方法调用时，形参N用来保存100
			}

【注意】
在Java中，实参的值永远都是拷贝到形参中，形参和实参本质上是两个实体。

【代码示例】： 交换两个整型变量

	public static void main(String[] args) {
        int a = 10;
        int b = 20;
        swap(a, b);
        System.out.println("main中的: a = " + a + " b = " + b);
    }
    public static void swap(int x, int y) {
        int tmp = x;
        x = y;
        y = tmp;
        System.out.println("swap中的: x = " + x + " y = " + y);
    }

其运行结果：

我们可以看到，使用swap函数交换后，形参x和y的值发生了改变，但是main方法中的a和b还是交换之前的值，没有交换成功。
【原因分析】
形参的改变并没有改变形参。
实参a和b是main方法中的两个变量，其空间在main方法的栈（一块特殊的内存）中。
而形参x和y是swap方法中的两个变量，x和y的空间在swap方法运行时的栈中。
因此：实参a和b与形参x和y是两个没有任何关联性的变量。在swap方法调用时，只是将实参a和b中的值拷贝了一份传递给了形参x和y， 因此对形参x和y的操作不会对实参a和b产生任何影响。

注意：对于基础类型 来说，形参相当于实参的拷贝，即传值调用 。

【解决方法】
可以用传引用类型参数数组（治标不治本）或 学习了类和对象解决，后续我们再写。

二、方法重载

1. 方法重载

Java允许在一个程序中定义多个名称相同，但是参数的类型或者个数不同的方法，这就是方法的重载。

 	public static double sum(double a,double b) {
        return a+b;
    }
    
    public static double sum(int b,double a,double c) {
        return a+b+c;
    }

【方法重载条件】

1. 方法名必须相同；
2. 参数列表必须不同（参数的个数不同、参数的类型不同、类型的次序必须不同）；
3. 与返回值类型是否相同无关。

2. 方法签名（了解）

为什么方法中不能定义两个名字一样的变量，为什么类中能定义方法名相同的方法？
我们可以认为一个方法在背后其实都是有名字的。
方法签名即：经过编译器修改过之后方法最终的名字。具体方式：方法全路径名+参数列表+返回值类型，构成方法完整的名字。

三、递归

1. 递归的概念

【生活中的故事】
从前有座山，山上有座庙，庙里有个老和尚给小和尚讲故事，讲的就是：
“从前有座山，山上有座庙，庙里有个老和尚给小和尚讲故事，讲的就是：”
“从前有座山…”
…“
上面的故事的特征是：自身中又包含了自己。该种思想在数学和编程中非常有用，因为有些时候，我们遇到的问题直接并不好解决，但是发现将原问题拆分成其子问题后，子问题又相同的解法，等子问题解决之后，原问题就迎刃而解了。

【递归的概念】
一个方法在执行过程中调用自身, 就称为 "递归。

【递归的条件】

1. 自己调用自己；
2. 有一个终止条件，也可以说起始条件；
3. 最难的地方就是如何能够确定递推公式！

【代码示例】 递归求N的阶乘

	public static int fac(int n) {
        if (n == 1) { //如果求1的阶乘
            return 1;
        }
        int tmp = n * fac(n-1);
        return tmp;
    }
    
    public static void main(String[] args) {
        System.out.println(fac(5));
    }
    

2. 递归的执行过程

我们拿上述求n的阶乘为例，当我们求3的阶乘的时候，执行过程如下图所示，
其中：红色代表递的过程，绿色代表归的过程。

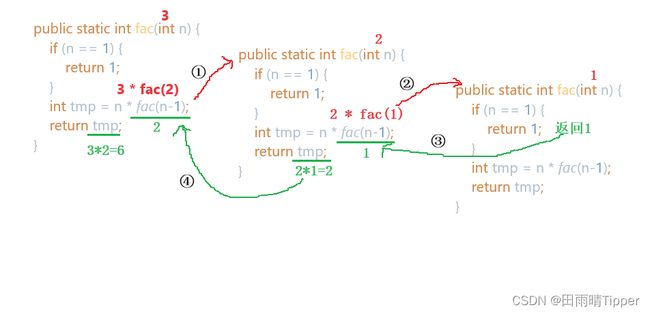
如上图所示，按照序号中标识的①-④的顺序执行，最后输出3！的结果为 6。
所有的递归都是发生在栈上的！！
这些程序的执行效率大大提高了！

3. 递归练习

代码示例1： 按顺序打印数字的每一位（例如1234，打印出1 2 3 4）

	public static void print(int num) {
		if (num > 9) {
		print(num / 10);
	}
		System.out.println(num % 10);
}

代码示例2： 递归求 1 + 2 + 3 + … + 10

	public static int sum(int num) {
		if (num == 1) {
		return 1;
	}
		return num + sum(num - 1);
}

代码示例3： 写一个递归方法，输入一个非负整数，返回组成它的数字之和，例如，输入1729，则应该返回1+7+2+9，它的和是19

	public static int sum(int num) {
		if (num < 10) {
		return num;
	}
		return num % 10 + sum(num / 10);
}