最小二乘法
1. 关于牛顿法的疑惑
为什么这里使用到了海参矩阵就可以快速的收敛呢?
原因:
1. 当一个位置斜率变化较大时,说明海参矩阵的值比较大(注意是斜率变化,不是函数值变化),那相应的inv(H)的值就会比较小,这个时候步进会慢些
2. 当一个位置比较平缓,斜率变化较小时,说明H矩阵值小,相应的inv(H)会比较大,步进会比较大
上述两点,相对于梯度下降法来说,尤其好理解的是,平缓区域的时候,梯度下降法步进会很慢,收敛也就相应的比较慢,但是牛顿法却很快
2. 关于初始值的疑惑
为什么拟合一定要有一个初始值,既然迭代一定会逼近一个极值的话,那不是不需要一个初始值,随便指定一个值不就好了?
个人理解,如果有错误,烦请指正,谢谢~~
其实,如果是求一个函数模型的极值点的话,是可以的,为什么,因为你选择的点一定能带入公式得到一个值(不说那些奇异的函数,比如 xxx/a,然后给a一个0的初始值,这里仅供理解),然后逐步迭代就好了。
但是拟合的话,就不同了
咦?不对呀,写着写着突然感觉不对,因为最小二乘拟合的话,也是一个函数呀
比如需要拟合的函数是
那对于这个函数 f 来说,不一样的可以随意估计一个初始值然后让它迭代收敛吗?
上面需要预估4个参数,A、s、t0、u
是不是自己在实现过程中,预估参数太多导致摁下葫芦起了瓢,才导致的不能够随意指定初始值的?
测试步骤:
1. 按照A、s、t0、u生成一个标准的曲线
2. 将标准曲线的值,和生成曲线的A、s、t0输入到LM算法中,u设置一个别的值
结果:
无法预估出结果,为什么?
3. 仿真具体过程
a. 代码:
clc;clear;close all;
%% 模拟数据
AUC = 100;
miu = 3;
std_var = 1.0; % 1
C = 0;
t0 = 0;
[x, tic_Src, origin_curve] = GenTicCurve(AUC, t0, miu, std_var, C);
plot(origin_curve, 'Linewidth',2);
hold on;
%%
simu_curve = origin_curve;
x_input = x;
init_u = 1;
ParamContrl = 0;
[new_auc, new_t0, new_c, new_s, new_u] = gradinent_descent(AUC, t0, std_var, init_u, C, x, simu_curve, ParamContrl);
new_curve = new_auc ./ (sqrt(2*pi)*new_s*(x_input-new_t0)) .* exp(-(log(x_input-new_t0) - new_u).^2 / (2 * new_s^2)) + new_c;
plot(new_curve, 'Linewidth',1);title(strcat('u=',num2str(init_u), ", newu=", num2str(new_u)));
function [x, ticCurve, origincurve] = GenTicCurve(AUC, t0, miu, phi_square, C)
t = 1 : 500;
for i=1:length(t)
if t(i)<=t0
I_lognormal(i) = C;
temp1(i) = 0;
temp2(i) = 0;
else
temp1(i) = exp(-(log(t(i)-t0)-miu)^2/(2*phi_square));
temp2(i) = AUC/(sqrt(2*pi)*sqrt(phi_square)*(t(i)-t0));
I_lognormal(i) = temp2(i)*temp1(i)+C;
end
end
x = t;
ticCurve = I_lognormal;
origincurve = ticCurve;
end
function [new_auc, new_t0, new_c, new_s, new_u] = gradinent_descent(AUC, t0, s, u, C, x, y, ParamContrl)
% 这个lr超参得非常慎重, 稍有不慎, 就会导致收敛不了.各位读者可以试试调一调lr.
lr = 0.01;
loss = 1000.0;
iter_count = 0;
max_iter_count = 50000;
samples = length(x);
t = x;
diff_u_change = [];
chang_u_model_curve = [];
for k = 1:100
exp_res = exp(-(log(t-t0) - k).^2 ./ (2 * s^2));
diff_u_value = -( AUC*exp_res*sqrt(2/pi) .* (C - AUC*exp_res./(sqrt(2*pi)*s*(t-t0)) + y) .* (-k + log(t-t0)) ) ./ (s^3*(t - t0));
k_diff_u = sum(diff_u_value);
diff_u_change(k) = k_diff_u;
chang_u_model_curve(k, :) = AUC./(s*(t-t0)*sqrt(2*pi)) .* exp_res + C;
end
while loss > 0.00001 && iter_count < max_iter_count
% 根据预测参数值s, u, 估计函数值pred_y
exp_res = exp(-(log(t-t0) - u).^2 ./ (2 * s^2));
pred_y = AUC./(s*(t-t0)*sqrt(2*pi)) .* exp_res + C;
loss = sum((y - pred_y).^2) ./ (2 * samples);
du_part_1 = -( AUC*exp_res*sqrt(2/pi) .* (C - AUC*exp_res./(sqrt(2*pi)*s*(t-t0)) + y) .* (-u + log(t-t0)) ) ./ (s^3*(t - t0));
dF_du = sum(du_part_1) / (2*samples);
jacobian = [dF_du]
u = u - lr * jacobian(1);
iter_count = iter_count + 1;
end
new_u = u;
new_auc = AUC;
new_t0 = t0;
new_c = C;
new_s = s;
end上面代码中,首先只让算法预估一个参数,miu(其实就是估计函数中的u),其他参数都固定成最优值(即生成曲线时候的值),且生成的曲线不添加任何噪声
b. 预估方向
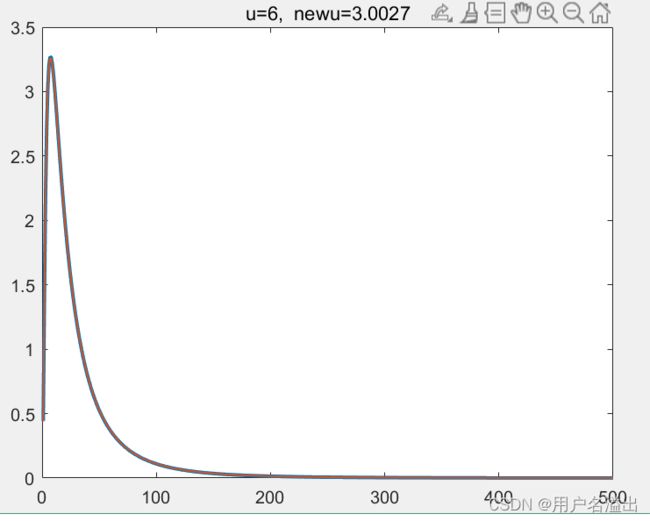
理想情况下来说,不管u是设置的什么初始值,u的值都应该在迭代过程中趋向于初始值3,但是测试的过程中会发现,在u的值初始化6的时候,结果
图像title上的u表示初始化的值,newu表示拟合出来的值, 可以发现,预估的曲线,在u = 1~6的时候,基本和源曲线是一致的,但是到u初始化到7的时候,曲线就无法进行拟合了,且在7的时候,拟合出来的值比7还大,即是往正确值相反的方向拟合的。
为什么呢?
c. 不同u的拟合方向查看
下面就是分析,为什么6的时候还是好的,但是到7就不行了,拟合方向是由U的一阶导数决定的,查看不同U的时候(U设置为1~100),导数曲线,即上述代码中的这部分
相应的曲线:
可以发现,在U的6的时候,斜率是正的,那拟合方向就是 小于6 的方向(实际值是3,所以是正确的方向),但是U = 7的时候,斜率是负数,拟合方向是 大于7的方向,这个方向是错误的。
为什么呢?
d. 原因分析
之所以出现上述情况,其实还是之前说的,如果是在求一个固定曲线的极值的时候,不管初始值是什么,只要曲线是固定的,那就一定会趋向于极值的方向进行迭代(注意这里的迭代就是我们的y= ***x的x变量),但是上述问题是拟合问题
我们并不是通过修改y=***x中的x值进行极值求解,而是在不断地迭代中更新***中的其他参数,比如我们仿真中的U参数
U参数的变化,会导致曲线本身发生变化,才会导致前面问题
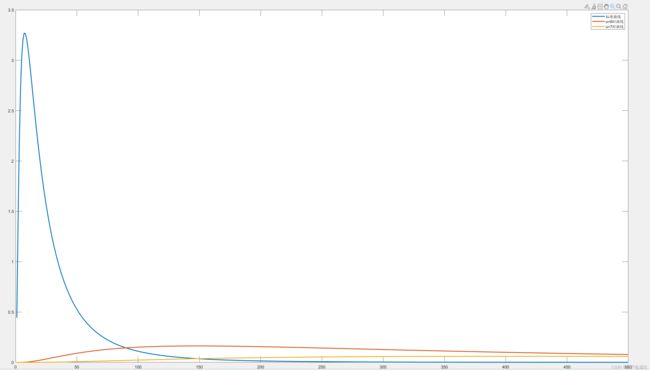
上图是标准曲线,U的6和7时生成的曲线对比
意味着,在U=6时的曲线进行偏导运算,带入各个参数得到的变化率是 >0的
在U=7时的曲线进行偏导运算,带入各个参数得到的变化率是 <0的
怎么解决这个问题呢?