数据结构——栈
数据结构——栈
-
- 一、理解栈
- 1. 栈的定义
- 2. 什么是 Java 虚拟机栈
- 3. 什么是栈帧
- 二、测试 Java 实现栈的方法
-
- 测试一
- 测试二
- 三、通过顺序表实现自己的栈
-
- 创建一个类 Stack 表示栈中的情况
- 创建一个类 Test 用来测试对栈的操作
- 测试一
- 测试二
- 思考用什么结构实现栈最优?
- 四、通过OJ题深入理解栈
-
- 题目一 出栈的输出序列判断
- 题目二 栈的压入、弹出序列
- 题目三 中缀表达式 与 后缀表达式
- 1. 中缀表达式 转 后缀表达式
- 2. 通过后缀表达式求出中缀表达式的值
- 3. OJ 题
- 题目四 有效的括号
- 题目五 最小栈
- 方法一:利用最小栈
- 方法二:直接利用顺序表实现栈
一、理解栈
1. 栈的定义
栈是限定仅在表尾进行插入和删除操作的线性表。
栈中的数据的特点:先进后出,后进先出。
在下图我们可以看到,我们只能对栈顶进行插入和操作,通俗的说,栈只能实现尾插尾删。

2. 什么是 Java 虚拟机栈
Java 虚拟机栈是 JVM 中的一块内存,该内存一般用来存放,局部变量等等…
3. 什么是栈帧
调用函数的时候,我们会为这个函数开辟一块内存,叫做栈帧,而开辟内存的场所就在 Java 虚拟机栈 之中。
二、测试 Java 实现栈的方法
测试一
程序清单1:
//测试 push、pop、peek、isEmpty 方法
public class Test1 {
public static void main(String[] args) {
Stack<Integer> stack = new Stack<>();
stack.push(1);
stack.push(3);
stack.push(5);
stack.push(7);
stack.push(9);
System.out.println(stack);
System.out.println(stack.pop()); //弹出栈顶的元素,并删除此元素
System.out.println(stack);
System.out.println(stack.peek()); //查看栈顶的元素,不删除此元素
System.out.println(stack.peek());
System.out.println(stack);
System.out.println(stack.isEmpty());
}
}
输出结果:
测试二
程序清单2:
//测试 search 方法
public class Test2 {
public static void main(String[] args) {
Stack<Integer> stack = new Stack<>();
stack.push(1);
stack.push(3);
stack.push(9);
stack.push(7);
stack.push(9);
System.out.println(stack.search(9));
System.out.println(stack.search(3));
System.out.println(stack.search(2));
//search() 方法从栈顶开始找元素,
//如果找到栈顶第一个元素就返回1,找到第二个元素就返回2...
//找不到就返回-1
}
}
输出结果:
三、通过顺序表实现自己的栈
创建一个类 Stack 表示栈中的情况
程序清单3:
import java.util.Arrays;
public class Stack{
public int[] elem;
public int usedSize;
public Stack() {
elem = new int[10];
}
//入栈
public void push(int data){
if(isFull() == true){
expansion();
}
elem[usedSize] = data;
usedSize++;
}
//判断栈是否已满
public boolean isFull(){
if(usedSize == elem.length){
return true;
}else {
return false;
}
}
//扩容
public void expansion(){
elem = Arrays.copyOf(elem,elem.length*2);
}
//移除栈顶的一个元素
public int pop(){
if(isEmpty() == true){
throw new RuntimeException("栈为空!");
}
int ret = elem[usedSize-1];
elem[usedSize-1] = 0;
usedSize--;
return ret;
}
//访问栈顶的一个元素
public int peek(){
if(isEmpty() == true){
throw new RuntimeException("栈为空!");
}
return elem[usedSize-1];
}
//判断栈是否为空
public boolean isEmpty(){
if(usedSize == 0){
return true;
}else {
return false;
}
}
//寻找栈中的某个元素
public int search(int findData){
int size = usedSize;
for (int i = usedSize - 1; i >= 0 ; i--) {
if(elem[i] == findData){
return size - i ;
}
}
return -1;
}
//打印栈中的所有元素
public void print(){
for (int i = 0; i < usedSize; i++) {
System.out.print(elem[i] + " ");
}
System.out.println();
}
}
创建一个类 Test 用来测试对栈的操作
测试一
程序清单4:
public class Test4 {
public static void main(String[] args) {
Stack stack = new Stack();
stack.push(1);
stack.push(3);
stack.push(5);
stack.push(7);
stack.push(9);
stack.print();
System.out.println(stack.pop());
stack.print();
System.out.println(stack.peek());
System.out.println(stack.peek());
stack.print();
System.out.println(stack.isEmpty());
}
}
输出结果:
测试二
程序清单5:
public class Test5 {
public static void main(String[] args) {
Stack stack = new Stack();
stack.push(1);
stack.push(3);
stack.push(9);
stack.push(7);
stack.push(9);
System.out.println(stack.search(9));
System.out.println(stack.search(3));
System.out.println(stack.search(2));
}
}
输出结果:
思考用什么结构实现栈最优?
刚刚我们自己通过顺序表实现了栈的结构,那么,我们可以使用单链表实现栈的结构吗?
答:可以。但是,有区别。
通过顺序表(数组实现栈时),入栈和出栈的复杂度都为 O(1),因为我们只要考虑尾插、尾删即可,很方便就能对栈顶的元素进行直接操作。
但是,通过单链表实现栈时,当我们头插头删的时候,入栈和出栈的复杂度都为 O(1),而我们进行尾插尾删的时候,我们都要进行遍历链表,找到链表的最后一个节点,此时入栈和出栈的复杂度都为 O(n) 。
而我们通过双向链表实现栈时,不论是头插头删、尾插尾删,入栈和出栈的复杂度都为 O(1),因为双向链表某个节点总有前驱节点的地址。
四、通过OJ题深入理解栈
题目一 出栈的输出序列判断
- 一个栈的入栈顺序是 a b c d e,则栈不可能的输出序列是:( C )
A. e d c b a
B. d e c b a
C. d c e a b
D. a b c d e
一个数据可以入栈,也同时可以出栈,先入栈的数据可以事先出来,事先入栈的元素也可以最后出来。并且遵循先进后出原则。
题目二 栈的压入、弹出序列
牛客网链接
程序清单6:
import java.util.*;
public class Solution {
public boolean IsPopOrder(int [] pushA,int [] popA) {
Stack<Integer> stack = new Stack<>();
int j = 0;
for(int i=0; i<pushA.length; i++){
stack.push( pushA[i] );
while( !stack.isEmpty() && stack.peek() == popA[j] ){
stack.pop();
j++;
}
}
return stack.isEmpty();
}
}
思路:
① 理解 pushA 数组是压栈数组,popA 数组是出栈数组。
② 通过 for 循环遍历 pushA 数组,不断地往 stack 栈中放入数据,数据通过数组下标 i 记录。
③ 与此同时,通过 while 循环判断栈最顶部的数据是否与 popA 数组的 j 下相等,若相等,则执行出栈操作。
④ 返回的时候,若栈为空,那么就符合出栈的逻辑,反之,不符合数据结构的逻辑。
图解分析:
下图为两种情况,只要考虑到这两种情况,那么就能将此题做出来了。
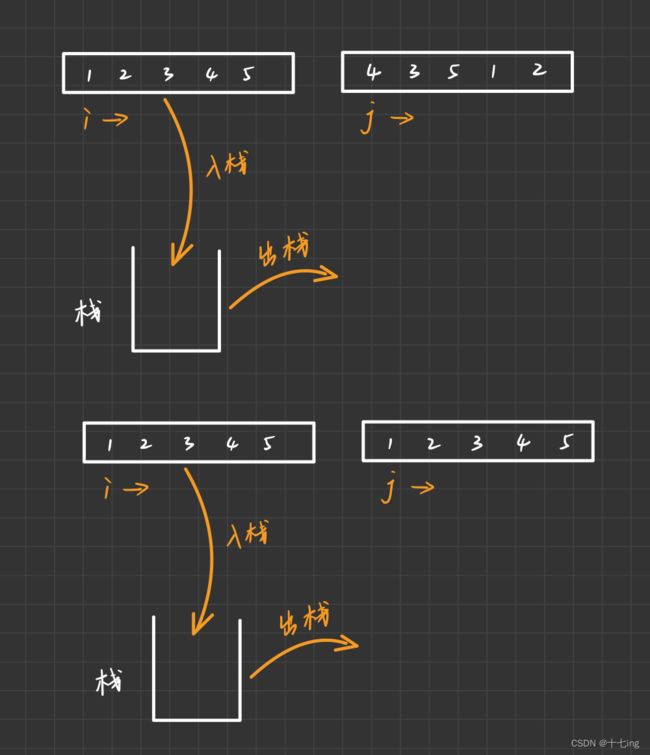
这里,我们需要注意一下程序清单1中,while 循环的条件:
while( !stack.isEmpty() && stack.peek() == popA[j] )
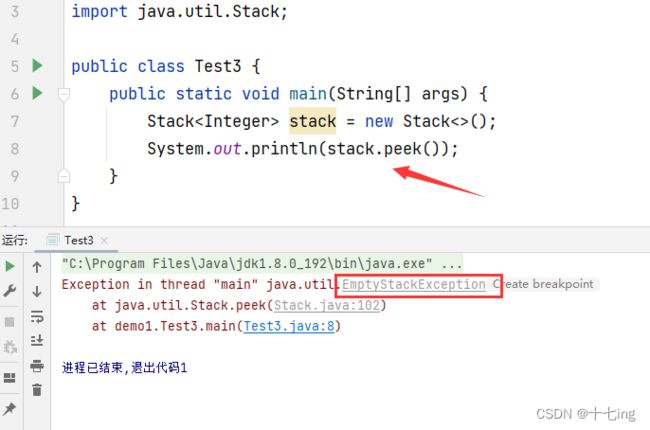
其中一条就是栈中的数据不能为空,否则我们使用 stack.peek( ) 访问栈中数据时会抛出异常,因为我们猜想:栈在源代码中,就是通过数组实现的,如果数组长度为0,我们再去访问元素,这就会造成数组越界!下图是我通过 IDEA 验证出来的结果:
题目三 中缀表达式 与 后缀表达式
先说明一下中缀表达式和后缀表达式之间的转换。
如下图:中缀表达式:(1 + 4) * 3 - 2
1. 中缀表达式 转 后缀表达式
① 在每一层运算加上圆括号(本身已有圆括号就不用重复加了)
② 将每个操作符移至每一层圆括号的后面
③ 把所有圆括号去掉
2. 通过后缀表达式求出中缀表达式的值
(1 + 4) * 3 - 2 //中缀表达式
14 + 3 * 2 - //后缀表达式
利用栈:
① 将后缀表达式放入一个字符串数组中,开始遍历这个数组
② 创建一个栈
③ 遇到数字就入栈
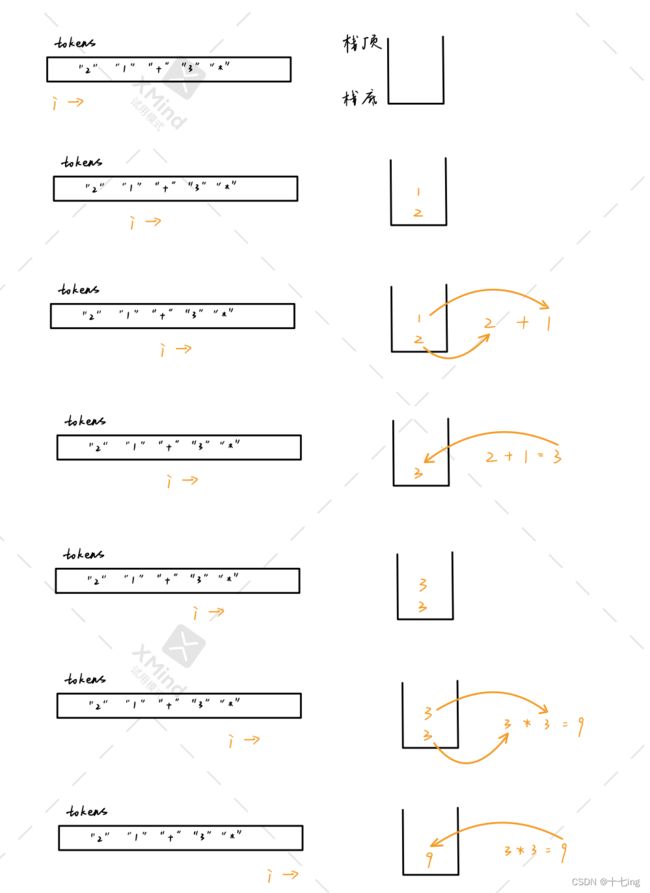
④ 遇到操作符就出栈,出栈就进行运算,先出栈的放在操作符的右边,后出栈放在操作符的左边。将出栈的两个元素计算后,继续入栈,并重复以上操作。
3. OJ 题
其中后缀表达式又称为逆波兰表达式
leetcode 150
程序清单7:
class Solution {
public int evalRPN(String[] tokens) {
Stack<Integer> stack = new Stack<>();
for(int i =0;i<tokens.length; i++){
String val = tokens[i];
if(judge(val) == false){
int n = Integer.parseInt(val);
stack.push(n);
}else{
int num2 = stack.pop();
int num1 = stack.pop();
switch(val){
case "+":
stack.push(num1 + num2);
break;
case "-":
stack.push(num1 - num2);
break;
case "*":
stack.push(num1 * num2);
break;
case "/":
stack.push(num1 / num2);
}
}
}
return stack.pop();
}
public boolean judge(String val){
if(val.equals("+") || val.equals("-") || val.equals("*") || val.equals("/")){
return true;
}else{
return false;
}
}
}
思路:
① 创建一个数组 tokens,里面都是字符串类型,表示我们需要操作的数据。
② 模拟一个栈 stack,准备用来存储整数。
③ 通过 for 循环遍历数组 tokens,并用 judge( ) 方法来判断每次拿到的是整数还是操作数 [ 加减乘除 ]。
④ 如果拿到的是整数,我们通过 stack.push( ) 方法进行入栈操作。
⑤ 如果拿到的是操作数,我们通过 stack.pop( ) 方法出栈操作,并使用栈顶的前两个整数进行数据运算。
⑥ 最终,我们 return 的值,也就是栈中最后一个值。
图解分析:
题目四 有效的括号
leetcode 20
程序清单8:
class Solution {
public boolean isValid(String s) {
Stack<Character> stack = new Stack<>();
for(int i=0; i< s.length(); i++){
char ch = s.charAt(i);
//如果遇到了左边的括号,那么就入栈
if(ch =='(' || ch =='{' || ch =='['){
stack.push(ch);
}
//如果遇到了右边的括号,那么就判断栈顶元素
else{
if(stack.isEmpty()){
//如果还未遍历完字符串,栈中已为空
//也就是右括号多于左括号的情况,直接返回 false
return false;
}
char top = stack.peek();
//判断左右括号是否匹配
if(top == '(' && ch == ')' || top == '{' && ch == '}' || top == '[' && ch == ']'){
stack.pop();
}else{
return false; //如果左右括号不匹配,直接返回 false
}
}
}
//当遍历完字符串时,栈中还有元素,也就是左括号多于右括号的情况,直接返回 false
if(!stack.isEmpty()){
return false;
}
return true;
}
}
思路:
正常情况:
((( )))
([ ])
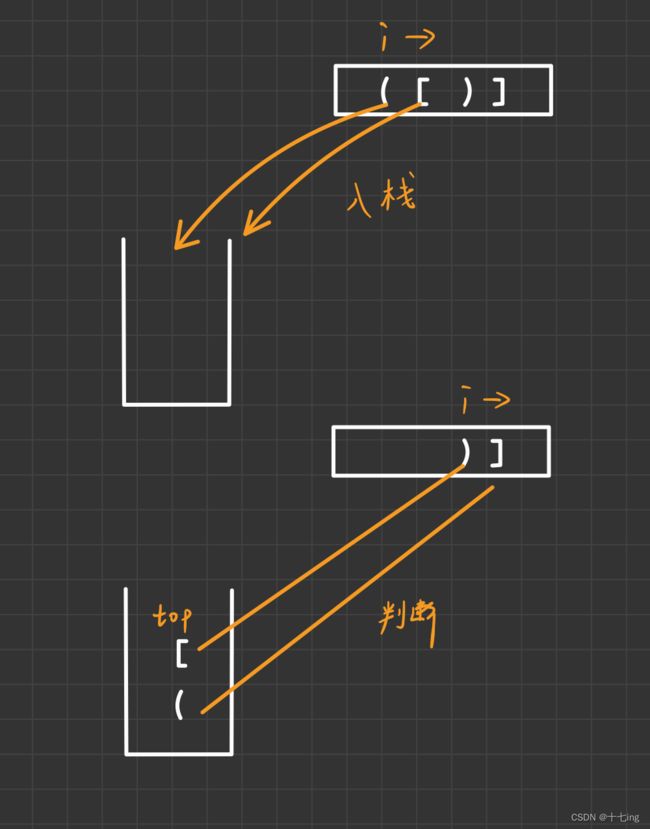
考虑三种特殊情况
① ((( ))
当遍历完字符串时,栈中还有元素,也就是左括号多于右括号的情况,直接返回 false
② (( )))
如果还未遍历完字符串,栈中已为空,也就是右括号多于左括号的情况,直接返回 false
③ ([ )]
如果左右括号不匹配,直接返回 false
分析图解:
题目五 最小栈
方法一:利用最小栈
leetcode 155
程序清单9:
class MinStack {
Stack<Integer> stack = new Stack<>();//普通栈
Stack<Integer> minStack = new Stack<>();//最小栈
public MinStack() {
}
public void push(int val) {
int topVal = stack.push(val);
//若最小栈为空时,往最小栈放元素
//若最小栈不为空,就要判断情况,
//如果普通栈的栈顶元素值 > 最小栈的栈顶元素值,那么就不往最小栈放元素
if(minStack.isEmpty() || topVal <= minStack.peek()){
minStack.push(topVal);
}
}
public void pop() {
int topVal = stack.pop();
//如果两个栈栈顶的元素是相同的,那么就删除最小栈的栈顶元素
if(topVal == minStack.peek()){
minStack.pop();
}
}
public int top() {
return stack.peek();
}
public int getMin() {
return minStack.peek();
}
}
思路:
(1)入栈时
① 创建两个栈,一个是普通栈 stack ,一个是最小栈 minStack。
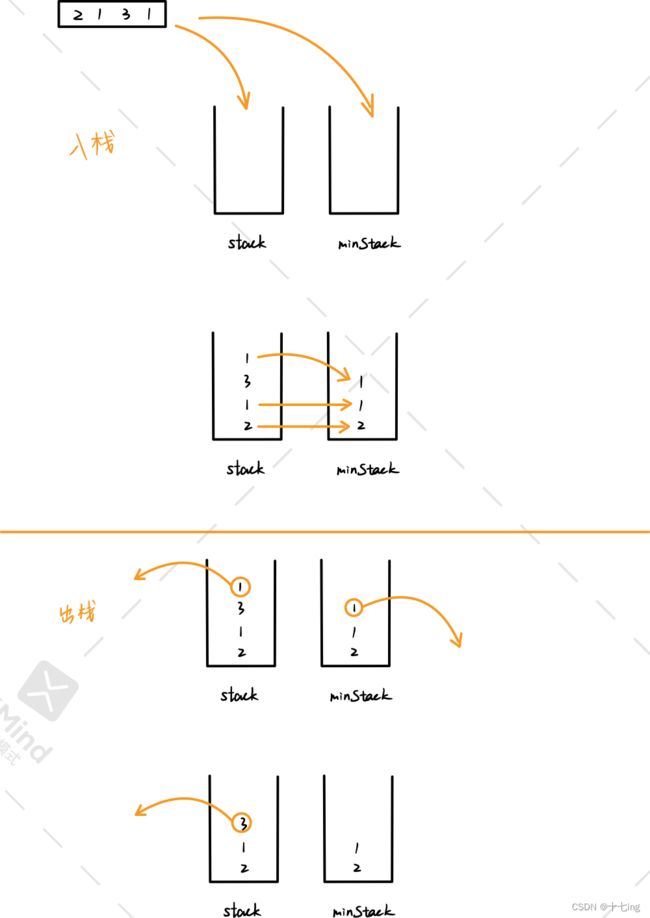
② 遇到的每个元素都要往普通栈中放,与此同时,若最小栈为空时,往最小栈放元素;若最小栈不为空,且普通栈的栈顶元素值 <= 最小栈的栈顶元素值,那么就往最小栈放元素。因为我们要保证栈顶为最小元素,方便我们拿出元素。
(2)出栈时
① 首先肯定要将普通栈的栈顶元素弹出,与此同时,若普通栈栈顶与最小栈栈顶的元素是相同的,那么就删除最小栈的栈顶元素。
试想,假设普通栈移除的是最小的元素1,如果不把最小栈的元素1移除,那么最后 getMin() 方法返回的就很可能是大于1的元素,这样就不符合逻辑了。因此我们可以把最小栈想象成一个虚拟的容器,它的存在只是用来记录普通栈的元素。
不管我们实现入栈操作,还是出栈操作,目的只有一个:最小栈的栈顶永远是最小的元素。因为在 getMin( ) 方法中,我们必须实现【 在常数时间内检索到最小元素的栈 】。
图解分析:
方法二:直接利用顺序表实现栈
import java.util.*;
class MinStack {
ArrayList<Integer> list = new ArrayList<>();
public MinStack() {
}
public void push(int val) {
list.add(val);
}
public void pop() {
list.remove( list.size()-1 );
}
public int top() {
return list.get( list.size()-1 );
}
//遍历顺序表,找到最小值
public int getMin() {
int minVal = list.get(0);
for (Integer x:list) {
if(minVal > x){
minVal = x;
}
}
return minVal;
}
}