动态规划(详细解释)
日升时奋斗,日落时自省
目录
1、Fibonacci
2、字符串分割
3、三角矩阵
4、路径总数
5、最小路径和
6、背包问题
7、回文串分割
8、编辑距离
9、不同子序列
10、总结
DP定义:
动态规划是分治思想的延伸,通俗一点来说就是大事化小,小事化无的艺术
在将大问题化解为小问题的分治过程中,保存对着些小问题已经处理好的结果,并供后面处理更大规模的问题时直接使用这些结果
动态规划具备了以下三个特点
1.把原来的问题分解成了几个相似的子问题
2.所有的子问题都只需解决一次
3.存储子问题的解
动态规划的本质,是对问题状态的定义和状态转移方程的定义(状态以及状态之间的递推关系)
动态规划问题一般从以下四个角度考虑:
1.状态定义
2.状态间的转移方程定义
3.状态的初始化
4.返回结果
状态定义的要求:定义的状态一定要形成递推关系
适用场景:最大值/最小值 ,可不可行, 是不是,方案个数
以下用例题来 详细了解动态规划
1、Fibonacci
题目来源于牛客网:斐波那契数列_牛客题霸_牛客网
斐波那契数列,最常了解的方法是递归方法解决问题
那如果是动规的情况如何处理斐波那契数列,
代码解析(附加注释):
public int Fibonacci(int n){
//初始值
if(n<=0){
return 0;
}
//申请一个数组 ,保存子问题的解,题目要求从第项开始
int[] dp=new int[n+1];
//状态初识化
dp[0]=0;
dp[1]=1;
for(int i=2;i<=n;i++){
//状态转移方程
dp[i]=dp[i-1]+dp[i-2];
}
//处理dp动规就是
return dp[n];
}2、字符串分割
题目来源于牛客网:拆分词句_牛客题霸_牛客网
题目描述 :给定一个字符串和一个词典dict ,确定是否可以根据词典中的词分成一个或多个单词
比如给定字符串 s = "leetcode" 词典: dict=["leet" ,"code"]
给定的字符串可以被分解,并且词典中还是有的能组成s字符串
方法:动态规划
代码解析(附加注释):
public boolean wordBreak(String s, Set dict){
//此处0下标表示的 辅助值 看你需要什么条件才能开始
boolean[] F=new boolean[s.length()+1];
//初识化F(0) = true 只有初识化后才能走
F[0]=true;
for(int i=1;i<=s.length();i++){
for(int j=i-1;j>=0;--j){
//F(i) : substr(j+1,i) 进行判定是否能在词典中找到
//以下也是动态转移方程 :
if(F[j]&&dict.contains(s.substring(j,i))){
F[i]=true;
break;
}
}
}
//因为以上创建对象的时候 动规返回 F[最后一个位置]
return F[s.length()];
} 3、三角矩阵
题目来源于牛客网:三角形_牛客题霸_牛客网
题目描述 : 给定一个三角矩阵 ,找出自顶向下的最短路径和,每一步可以移动到下一行的相邻数字,比如给定下面一个三角矩阵,自顶向下的最短路径和
方法:动态规划
状态:子状态:
从(0,0) 到 (1,0),(1,1),(2,0),,,,(n,n)的最短路径和F(i,j),从(0,0)到(i,j)的最短路径和
状态递推(状态转移方程):
F(i,j)=min(F(i-1,j-1),F(i-1,j)+triangle[i][j])
初始值: F(0,0)也就是数组开始位置 triangle[0][0]
以下是三种情况:并且每种情况都是动态规划的转移方程
代码解释(附加注释):
public int minimumTotal(ArrayList> triangle){
if(triangle.isEmpty()){
return 0;
}
List> min=new ArrayList<>();
//将所有数组的开始添加一个 顺序表
for(int i=0;i());
}
min.get(0).add(triangle.get(0).get(0));//将开始位置 添加到最小路径中
for(int i=1;i 4、路径总数
题目来源于牛客网:不同路径的数目(一)_牛客题霸_牛客网
题目描述:
在一个m*n的网格的左上角有一个机器人,机器人在任何时候只能向下或者向右移动,机器人试图到达网格的右下角,有多少可能的路径
动态规划:
代码解释(附加注释):
public int uniquePaths(int m,int n){
List> pathNum=new ArrayList<>();
//申请 F(i,j)空间 初始化
for(int i=0;i());
//将每列第一个元素都进行 加 1 图解详细 ,仔细观看
pathNum.get(i).add(1);
}
for(int i=1;i 5、最小路径和
题目来源于力扣:力扣
题目描述:给定一个m*n的网格 ,网格用非负数填充,找到一条从左上角到右下角的最短路径
注:每次只能向下或者向右移动 ,相当于是路径总数的基础上找到一个最短的路径
方法:动态规划
状态:
子状态: 从(0,0)到达 (1,0),(1,1),(2,1) ...(m-1,n-1)
minsum(i,j):从(0,0) 到达minsum(i,j)的最短路径
状态转移方程:
minsum[i][j]=Math.min(minsum[i-1,j],minsum[i,j-1])+minsum[i][j]
初始化值:
minsum[0][0]=(0,0)
特殊情况:第0行 和 第0列
minsum(0,i)=minsum(0,i-1)+(0,i)
minsum(i,0)=minsum(i-1,0)+(i,0)
代码解析(附加注释):
public int minPathSum(int[][] minsum){
int row=minsum.length;
int col=minsum.length;
//如果行还是列有一个为空 返回为0
if(row==0||col==0){
return 0;
}
//F(0,0) F(0,i) F(i,0) 初始化
for(int i=1;i6、背包问题
题目来源于炼码:LintCode 炼码
题目描述:
有n个物品和一个大小为m的背包,给定数组A表示每个物品的大小和数组V表示每个物品的价值。
问最多能装下背包的总价值是多大?
状态:
F(i,j):前i个物品放入大小为 j 的背包中所获得的最大价值
状态转移方程过程:
对于第i个商品,有一种例外,装不下,两种选择,放或者不放,如果装不下:此时的价值与前i-1的个的价值是一样的,表示不装
F(i,j)=F(i-1,j)
如果可以装入,需要在两种选择中找到最大的
F(i,j)=max(F(i-1,j),F(i-1,j-A[i])+V[i]) 注:此处看的不是那么清楚,一会看一下图解
F(i-1,j):表示不把第i个物品放入背包中,所以它的价值就是前i-1个物品放入大小为j的背包的最大价值
F(i-1,j-A[i])+V[i] :表示把第i个物品放入背包中,价值增加V[i] ,但是需要腾出 j-A[i]的大小放第i个商品
初始化:第0行 和第0列都为0 表示没有装物品的价值都为0
代码解析(附加注释):
public int backPackII(int m,int[] A,int[] V){
int num=A.length;
if(m==0||num==0){
return 0;
}
//需要辅助值 作为准备 数组中 num+1 表示 物品大小 m+1 表示价值
int[][] maxValue=new int[num+1][m+1];
//初始化所有位置为0 第一行 和 第一列都为0 初识条件
for(int i=0;i<=num;i++){
maxValue[i][0]=0;
}
for(int i=1;i<=m;i++){
maxValue[0][i]=0;
}
for(int i=1;i<=num;i++){
for(int j=1;j<=m;j++){
//第i个商品在A中对应的索引为 i-1 i从1开始
//如果第i个商品大于j 说明放不下 所以(i,j)的最大价值 和 (i-1,j)相同
if(A[i-1]>j){
//当前物品体积 大于 当前容量 就说明装不下,把原来的继承下来就行
maxValue[i][j]=maxValue[i-1][j];
}else{
//如果可以装下,分两情况 装或者不装
//如果不装 ,即为 (i-1,j)
//如果装 , 需要腾出放第i个物品大小的空间:j-A[i-1],能装之后的最大价值即为原有价值加上
// maxValue[i - 1][j - A[i - 1]] + V[i-1]
//最后在装与不装中选出最大的价值
int newValue=maxValue[i-1][j-A[i-1]]+V[i-1];
//新值 与 原来值 进行比对
maxValue[i][j]=Math.max(newValue,maxValue[i-1][j]);
}
}
}
return maxValue[num][m];
}注:newValue=maxValue[i-1][j-A[i-1]]+V[i-1]; 创建数组时就已经了各加一个空间,第0行和第0列已经处理好了,占了一个位置,所以V[i-1]其实也就是V[i],因为二维数组整体加1如果还想要调用V[i] 此处就需要V[i-1]
7、回文串分割
题目来源于牛客网:分割回文串-ii_牛客题霸_牛客网
回文串:正读和反读都一样的字符串,比如level,noon字符串左右对称
题目描述:
给定一个字符串 s, 把 s 分割成一系列的子串,分割的每一个子串都为回文串返回最小的分割次数比如,给定 s="abb" 返回1 ,因为一次 cut 就可以产生回文分割[“a","bb"];
方法:动态规划
状态:
子状态:到 1,2,3,....n个字符需要的最小分割数
F(i):到第i个字符需要的最小分割数
状态递推(状态转移方程):
F(i) =min(F(i),1+F(j)) , F(i) 表示第i个字符需要的最小分割数, 就 j < i && j+1 到 i是回文串上式表示如果从j+1 到i 判断 为回文字符串,且已经知道从第 1 个字符串到第 j 个字符的最小切割数,那么只需要再切一次 ,就可以保证 1到j , j+1 到 i都为回文串
初始化 :
F(i) =i-1 表示最大切割数 : 单个字符需要切0次 ,因为单子符都为回文串(图解)
代码解释(附加注释):
public int mincut(String s){
int len = s.length();
if(len==0){
return 0;
}
//进行 判定该阶段的字符串 是不是 回文串
boolean[][] Mat=getMat(s);
int[] mincut=new int[len+1];
//F(i) 初始化
//F(0)=-1 必要项 如果没有这一项 ,对于 重叠字符串 “aaaa" 会产生错误的结果
for(int i=0;i<=len;i++){
mincut[i]=i-1; //此处针对特殊情况 就是全部字符串都是重复的 ,应对错失
}
for(int i=1;i<=len;i++){
for(int j=0;j=0;i--){
//到这开始 从一个一个来
for(int j=i;j 8、编辑距离
题目来源于牛客网:编辑距离_牛客题霸_牛客网
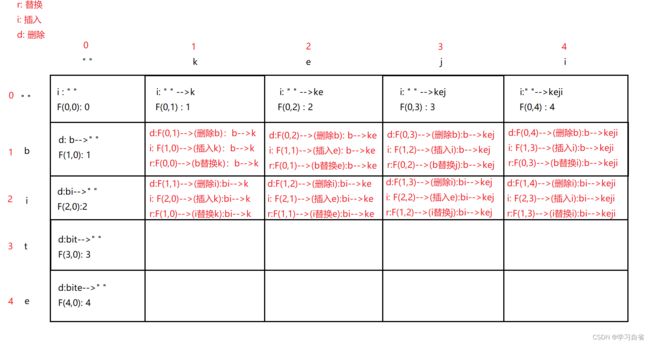
题目描述: 给定两个单词word1 和 word2、 找到最小的修改步数 ,把word1 转换成 word2,每一个操作记为一步 ,允许在一个word上进行如下3种操作:
(1)插入一个字符
(2)删除一个字符
(3)替换一个字符
编辑距离 是指两个字符串之间, 由一个转成另一各所需的最少编辑操作次数
方法: 动态规划
状态:
子状态 :word 1的前1,2,3,....m个字符转换成word2的前1,2,3,....n个字符需要的编辑距离
F(i,j):word1的前i个字符于word2 的前j个字符的编辑距离
状态递推(状态转移方程):
F(i,j) =min(F(i-1,j)+1,F(i,j-1)+1,F(i-1,j-1)+(word1[i]==word2[j]?0:1)) 注: 此处下面再解释
上式表示从删除,增加和替换操作中选择一个最小操作数
F(i-1,j):word1[1...i-1]于word2[1....j]的编辑距离 ,删除word1[i]的字符--->F(i,j)
F(i,j-1):word1[1....i]于word2[1....j-1]的编辑距离,增加一个字符--->F(i,j)
F(i-1,j-1):word1[1....i-1]于word2[1...j-1]的编辑距离 ,如果word1[i]与word2[j]相同,不做任何操作 ,编辑距离不变,如果word1[i]与word2[j]不同,替换word1[i]的字符为word2[j]--->F(i,j)
初始化:
初始化一定要是确定的值,如果这里不加入空串,初始值无法确定
F(i,0)=i :word 与空串的编辑距离 ,删除操作
F(0,i)=i: 空串与word的编辑距离 ,增加操作
放回结果:F(m,n) (图解没有完全 以下给出 可以找到规律)
代码注释(附加注释):
//word 与空串 之间的编辑距离为word 的长度
public int minDistance(String word1,String word2){
if(word1.isEmpty()||word2.isEmpty()){
return Math.max(word1.length(),word2.length());
}
int len1=word1.length();
int len2=word2.length();
//动态规划 需要辅助值 所以当前数组也多创建了一行
int[][] minDis=new int[len1+1][len2+1];
//F(i,j) 初始化 针对不同位置的东西
for(int i=0;i<=len1;i++){
minDis[i][0]=i;
}
for(int i=0;i<=len2;i++){
minDis[0][i]=i;
}
for(int i=1;i<=len1;i++){
for(int j=1;j<=len2;j++){
//F(i,j) =min (F(i-1,j)+1,F(i,j-1)+1,F(i-1,j-1)+(word1[i]=word2[j]?0:1))
minDis[i][j]=Math.min(minDis[i-1][j],minDis[i][j-1])+1;
if(word1.charAt(i-1)==word2.charAt(j-1)){
//字符相等 F(i-1,j-1) 编辑距离不变 与上次
minDis[i][j]=Math.min(minDis[i][j],minDis[i-1][j-1]);
}else{
//字符不相等 F(i-1,j-1) 编辑距离+1
// 因为不同 所以 当前位置的 与 上一位置+1 进行比较
minDis[i][j]=Math.min(minDis[i][j],minDis[i-1][j-1]+1);
}
}
}
return minDis[len1][len2];
}
9、不同子序列
题目来源于牛客网:不同的子序列_牛客题霸_牛客网
题目描述: 给定两个字符串S 和 T ,求S有多少个不同的子串 与T相同。S的子串定义为 S中任意去掉0个或者多个字符形成的串 子串可以不连续 ,但是相对位置不能变。
比如“ACE” 是“ABCDE” 的子串 ,但是“AEC” 不是
问题处理:S有多少个不同的子与T相同的个数
S[1:m] 中的子串与T[1:n]相同的个数 由S的前m个字符组成的子串与T的前n个字符相同的个数
状态:
子状态:由S的前1,2....m个字符组成的子串与T前1,2,.....n个字符相同的个数F(i,j):S[1;i]中的子串与T[1:j]相同的个数
在F(i,j):S[1:i]中的子串与T[1:j]相同的个数
状态递推(状态转移方程):
在F(i,j),处需要考虑S[i]=T[j]和S[i]!=T[j]这两种情况
当S[i]=T[j]:
1> :让S[i]匹配T[j],则F(i,j)=F(i-1,j-1)
2> :让S[i]不匹配 T[j] ,则问题就变为S[1:i-1] 中的子串与T[1:j]相同的个数 ,则F(i,j)=F(i-1,j)
故:S[i]=T[j]时,F(i,j)=F(i-1,j-1)+F(i-1,j)
当S[i]!=T[j]
问题退化为 s[1:i-1] 中的子串 与 T[1:j] 相同的个数
故,S[i]!=T[j] 时 F(i , j) =F(i-1,j)
初始化 :引入空串进行初始化
F(i,0)=1 -->S的子串与空串相同的个数 ,只有空串 与 空串相同
代码解析(附加注释):
public int numDistinct(String s,String T){
int slen=s.length();
int tlen=T.length();
int[][] numDis=new int[slen+1][tlen+1];
numDis[0][0]=1;
//F(i,j) 初始化第一行 剩余列的所有值为0
for(int i=1;i<=tlen;i++){
numDis[0][i]=0;
}
//F(i,0)=1 辅助值
for(int i=1;i<=slen;i++){
numDis[i][0]=1;
}
//每次都从1 开始 因为多创建一个空间 作为辅助值来提供帮助
for(int i=1;i<=slen;i++){
for(int j=1;j<=tlen;j++){
//s 的第i个字符与 T 的第j个字符相同
if(s.charAt(i-1)==T.charAt(j-1)){
numDis[i][j]=numDis[i-1][j]+numDis[i-1][j-1];
}else{
// s 的第i个字符与 T 的第j个字符不相同
//从S 的前 i-1 个字符中找子串 ,使子串 与 T的前j个字符相同
numDis[i][j]=numDis[i-1][j];
}
}
}
return numDis[slen][tlen];
}10、总结
动态规划 其实与贪心思想有点相似,都需要自己去看是否有规律可循。
(1)状态定义:其实就是设计动态规划的问题是啥
(2)状态转移方程:将文字定义来的状态转化为一个代码方程表示
(3)状态初始值 辅助值 是动态规划的起步 (根据动态方程来决定如何启动)