详谈时间复杂度
博客主页: A_SHOWY
系列专栏:力扣刷题总结录 数据结构 云计算
一、什么是时间复杂度
简单来说,时间复杂度描述的一个算法的运行时间,它其实是一个函数。通常会估算算法的操作单元数量f(n)代表程序消耗的时间,默认CPU的每个单元消耗时间相同。算法的操作单元数量和算法的执行时间增长率是相同的,称作算法的渐进时间复杂度,也就是O(f(n))。
二、什么是 ‘O’
其实O就是表示的是最坏情况下算法的运行时间,也就是算法的上界。
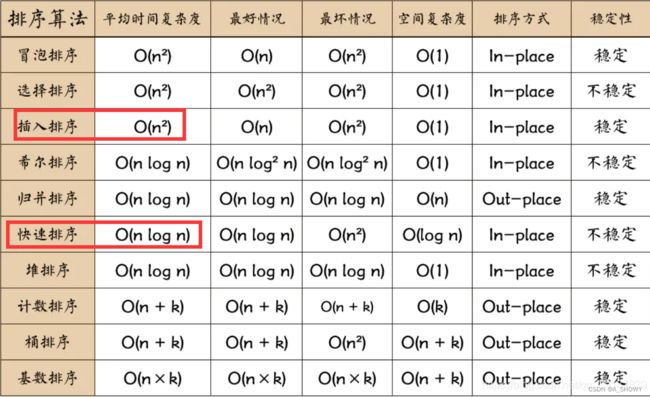
以插入排序和快速排序为例,插入排序很明显最坏的情况就是每次插入都要
最多次数比较所以最坏情况就是n方。
而快速排序最坏情况也是n方,但是业内都普遍说明的是O(nlogn),所以在这里所说的就是一般情况。
三、时间复杂度的一个基本排序
O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) < O(2n) < O(n!)
但是要注意当常数非常大时,常数也不得不进入考虑因素了。在一般情况下,我们都会对复杂的表达式进行化简,首先去掉系数,然后再保留最高项。
例:
O(5 * n^3 + 10 * n + 100)可以化简为
O(n^3)四、判断时间复杂度的例子
题目:找出n个字符串中相同的两个字符串(假设这里只有两个相同的字符串)。
方法1.暴力法
如果用暴力算法的话,除了n^2的遍历次数以外还要考虑字符串的比对,此题不比整型的比较,还要遍历一遍m(字符串的长度),所以时间复杂度为O(m * n * n)。
方法2.先排序
先对这n个字符串进行字典序排序(首字符),排完以后就是有序的n个字符串,然后相同的字符串就挨在一起,再遍历一遍n个字符串就可以了。
快速排序的时间复杂度是O(nlogn),同样需要考虑有m个字符串的长度,所以为O(m * n *logn),加上最后再遍历一遍,遍历的时候还要比较字符串。所以时间复杂度为O(m* n * logn + m *n)。化简以后就是O(m * n * logn),和暴力算法比较的话,还是方法二时间复杂度更低,所以先排序再遍历一遍的方式更快。当然这是分析的过程,如果考研题目的时间复杂度有具体的方法。分为一层循环两层循环多层循环等等,每种题型有特定的方法。
五、不要看到递归就觉得是O(logn)
例:求x的n次方
方法1.比较容易的思路 :
int function1(int x , int n)
{
int result = 1;//任何数的0次方都是1
for(int i =0; i < n; i++)
{
reult - result * x;
}
return result;
}此时不难看出这个方法的时间复杂度是O(n)
如何考虑使用递归
方法2.简单递归
int function2(int x, int n)
{
if(n == 0) {return 1;}
return function2(x,n-1) * x;
}
递归算法的时间复杂度本质上是要看: 递归的次数 * 每次递归中的操作次数。并不是直接无脑O(logn)。每次n-1,递归了n次时间复杂度是O(n),每次进行了一个乘法操作,乘法操作的时间复杂度一个常数项O(1),所以这份代码的时间复杂度是 n × 1 = O(n)。
方法3.变换递归
int function3(int x, int n) {
if (n == 0) return 1;
if (n == 1) return x;
if (n % 2 == 1) {
return function3(x, n / 2) * function3(x, n / 2)*x;
}
return function3(x, n / 2) * function3(x, n / 2);
}
这棵树上每一个节点就代表着一次递归并进行了一次相乘操作,所以进行了多少次递归的话,就是看这棵树上有多少个节点。但是如此分析看来,时间复杂度还是O(n)。
方法4.logn递归
int function4(int x ,int n)
{
if(x = 0) {reutrn 0;}
if(x = 1) {return x;}
int t = function4(x,n/2);//把这个递归的操作提取出来,减少递归次数
if((n % 2) == 1) {return t*t*x}
return t*t;
}可以看到这里每次只用一个递归调动,而且每次都是n/2,所以,这个递归算法的时间复杂度才是真正的 O(logn)。