粒子群算法调参支持向量回归进行预测（PSO-SVR）Python实现

目录

一、算法简介

二、示例

1.导入库包、数据以及数据预处理

2.利用粒子群算法调优参数gamma和C

3.模型训练与预测

4.对模型进行性能评估

5.结果展示

 三、代码总结

SVR.py

PSO_SVR.py

---

一、算法简介

---

SVR（支持向量回归）是一种有效的非线性回归方法，它可以通过寻找一组最优参数来拟合数据。粒子群算法是一种优化算法，可以用于找到最佳的SVR参数。

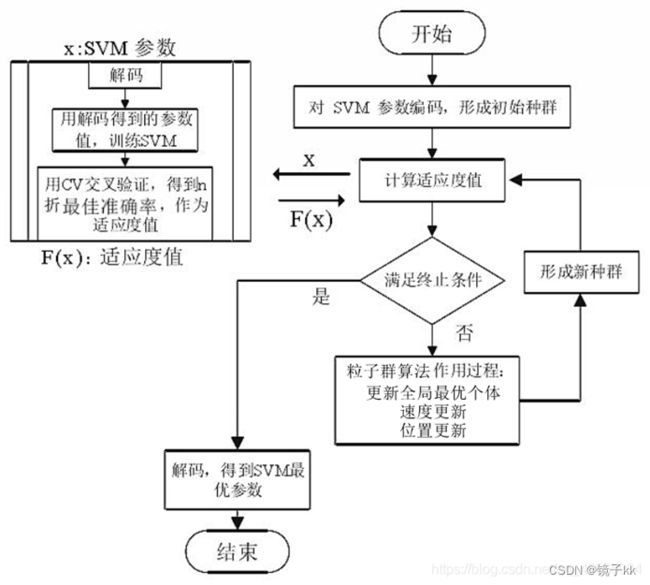
以下是使用粒子群算法进行SVR参数调优的步骤：

1. 确定SVR模型的核函数和参数范围。常用的核函数有线性核、多项式核和高斯径向基核。参数范围包括核函数参数、正则化参数等。

2. 定义粒子群算法的目标函数。在SVR预测中，通常使用均方误差（MSE）或均方根误差（RMSE）作为目标函数。

3. 初始化粒子群的位置和速度。每个粒子表示一组参数，位置表示参数的值，速度表示参数的变化方向和速率。初始化时，可以随机生成一组粒子，并将其位置和速度随机分配在参数范围内。

4. 计算每个粒子的适应度。将每个粒子的位置作为SVR模型的参数，运行模型并计算相应的目标函数值。

5. 更新粒子的位置和速度。根据每个粒子的适应度和全局最优粒子的位置，更新每个粒子的速度和位置。其中，全局最优粒子是历史上适应度最好的粒子。

6. 重复步骤4和5，直到满足收敛条件。收敛条件可以是达到最大迭代次数、目标函数值小于某一阈值等。

7. 将全局最优粒子的位置作为SVR模型的最优参数，重新运行模型并进行预测。

通过这种方法，可以找到最优的SVR参数，从而获得更准确的预测结果。

---

二、示例

本示例共涉及两个py文件，SVR.py和PSO_SVR.py

其中，PSO_SVR.py为粒子群算法调参的过程。

两者的关系为SVR.py调用PSO_SVR.py

---

1.导入库包、数据以及数据预处理

导入库包

import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt

## 设置属性防止中文乱码
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False

导入数据、数据预处理

#读取数据
data = pd.read_excel()
data = np.array(data)

#划分特征值与目标值
X =data[:,1:-1]
y =data[:,-1]

#将数据标准化
from sklearn.preprocessing import StandardScaler

# 创建一个标准化器对象
scaler = StandardScaler()

# 使用标准化器拟合和转换数据集
X = scaler.fit_transform(X)

# 将数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

2.利用粒子群算法调优参数gamma和C

为了代码简单好理解，PSO_SVR.py文件，编写粒子群算法相关函数

用主代码文件调用此py文件，最后返回调参完成的SVR模型

import numpy as np
from sklearn.svm import SVR
from matplotlib import pyplot as plt
import pyswarms as ps

np.random.seed(42)


# 适应度函数
def fitness_function(params, X, y, xt, yt):
    C, gamma = params
    svm_model = SVR(kernel='rbf', gamma=gamma, C=C)
    svm_model.fit(X, y)
    y_pred = svm_model.predict(xt)
    mse = np.mean((yt - y_pred) ** 2)
    return mse


# 优化函数
def optimize_svm(X, y, xt, yt, n_particles=100, n_iterations=100):
    def _fitness_function(params):
        fitness_values = []
        for p in params:
            fitness = fitness_function(p, X, y, xt, yt)
            fitness_values.append(fitness)
        return fitness_values

    # 参数边界
    bounds = (np.array([0.1, 0.01]), np.array([50.0, 10.0]))
    options = {'c1': 0.5, 'c2': 0.3, 'w': 0.9}

    cost_history = np.zeros(n_iterations)
    # 运行优化器进行参数优化
    optimizer = ps.single.GlobalBestPSO(n_particles=n_particles, dimensions=2, bounds=bounds, options=options)

    best_cost, best_params = optimizer.optimize(_fitness_function, iters=n_iterations)

    # 在每次迭代前保存代价值
    for i, cost in enumerate(optimizer.cost_history):
        cost_history[i] = cost


    # 根据优化结果建立最终的SVM模型
    C, gamma = best_params
    svm_model = SVR(kernel='rbf', gamma=gamma, C=C)
    svm_model.fit(X, y)
    print('最优参数：', best_params)
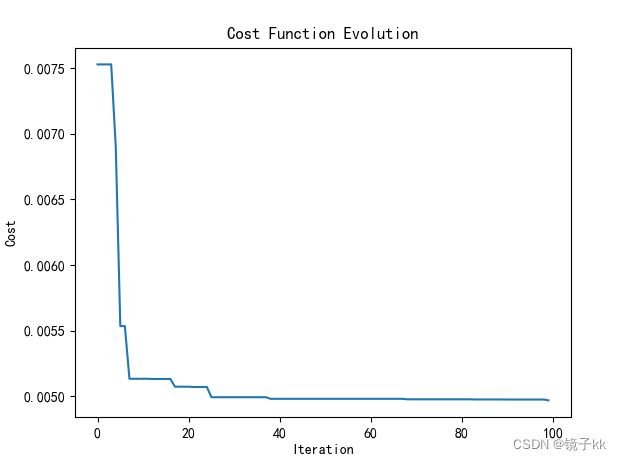
    # 绘制代价值变化曲线
    plt.plot(range(n_iterations), cost_history)
    plt.xlabel('Iteration')
    plt.ylabel('Cost')
    plt.title('Cost Function Evolution')
    plt.show()

    return svm_model

3.模型训练与预测

#调用PSO_SVR.py文件
import PSO_SVR
#获取返回的调参后的模型
svr = PSO_SVR.optimize_svm(X_train,y_train,X_test,y_test)
#训练
svr.fit(X_train, y_train)
#预测
result = svr.predict(X_test)

4.对模型进行性能评估

#计算模型在测试数据上的得分，通常使用R^2（决定系数）作为评估指标。
score = svr.score(X_test, y_test)

#存储测试数据的真实标签和预测结果
y_testRON = []
resultRON = []
for i in range(len(result)):
    y_testRON.append(y_test[i])
    resultRON.append(result[i])

# 计算了模型在训练数据上的得分。
score_train = svr.score(X_train, y_train)
result_train = svr.predict(X_train)

#存储训练数据的真实标签和预测结果
y_trainRON = []
resultRON_train = []
for i in range(len(result_train)):
    y_trainRON.append(y_train[i])
    resultRON_train.append(result_train[i])

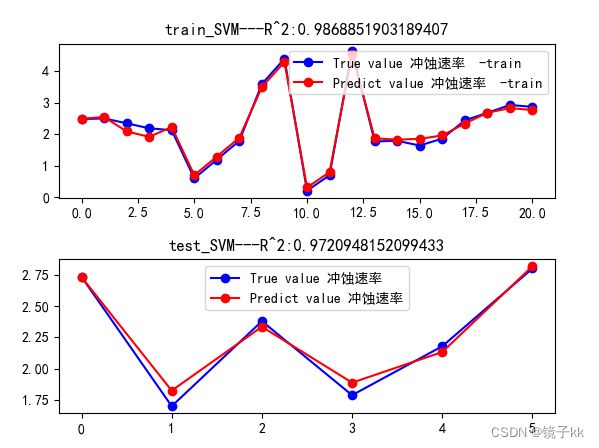
##可视化
fig = plt.figure()
fig.subplots_adjust(hspace=0.4)
plt.subplot(2, 1, 1)
plt.plot(np.arange(len(result_train)), y_trainRON, "bo-", label="True value 冲蚀速率  -train")
plt.plot(np.arange(len(result_train)), resultRON_train, "ro-", label="Predict value 冲蚀速率  -train")
plt.title(f"train_SVM---R^2:{score_train}")
plt.legend(loc="best")
plt.subplot(2, 1, 2)
plt.plot(np.arange(len(result)), y_testRON, "bo-", label="True value 冲蚀速率")
plt.plot(np.arange(len(result)), resultRON, "ro-", label="Predict value 冲蚀速率")
plt.title(f"test_SVM---R^2:{score}")
plt.legend(loc="best")
plt.show()

##可视化标准误差
# test
RON = np.array(resultRON)
# train
RONtrain = np.array(resultRON_train)

RE_RONtest = abs(y_testRON - RON) / y_testRON

RE_RONtrain = abs(y_trainRON - RONtrain) / y_trainRON

plt.figure()
plt.plot(np.arange(len(RE_RONtrain)), RE_RONtrain, "ro-", label="RE value 冲蚀速率  -train")
plt.plot(np.arange(len(RE_RONtrain), len(RE_RONtrain) + len(RE_RONtest)), RE_RONtest, "bo-",
         label="RE value 冲蚀速率  -test")
plt.title('Relative Error')
plt.legend(loc="best")
plt.show()

5.结果展示

 三、代码总结

---

SVR.py

import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt

## 设置属性防止中文乱码
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False

#读取数据
data = pd.read_excel()
data = np.array(data)

#划分特征值与目标值
X =data[:,1:-1]
y =data[:,-1]

#将数据标准化
from sklearn.preprocessing import StandardScaler

# 创建一个标准化器对象
scaler = StandardScaler()

# 使用标准化器拟合和转换数据集
X = scaler.fit_transform(X)

# 将数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)


#调用PSO_SVR.py文件
import PSO_SVR
#获取返回的调参后的模型
svr = PSO_SVR.optimize_svm(X_train,y_train,X_test,y_test)
#训练
svr.fit(X_train, y_train)
#预测
result = svr.predict(X_test)


#计算模型在测试数据上的得分，通常使用R^2（决定系数）作为评估指标。
score = svr.score(X_test, y_test)

#存储测试数据的真实标签和预测结果
y_testRON = []
resultRON = []
for i in range(len(result)):
    y_testRON.append(y_test[i])
    resultRON.append(result[i])

# 计算了模型在训练数据上的得分。
score_train = svr.score(X_train, y_train)
result_train = svr.predict(X_train)

#存储训练数据的真实标签和预测结果
y_trainRON = []
resultRON_train = []
for i in range(len(result_train)):
    y_trainRON.append(y_train[i])
    resultRON_train.append(result_train[i])

##可视化
fig = plt.figure()
fig.subplots_adjust(hspace=0.4)
plt.subplot(2, 1, 1)
plt.plot(np.arange(len(result_train)), y_trainRON, "bo-", label="True value 冲蚀速率  -train")
plt.plot(np.arange(len(result_train)), resultRON_train, "ro-", label="Predict value 冲蚀速率  -train")
plt.title(f"train_SVM---R^2:{score_train}")
plt.legend(loc="best")
plt.subplot(2, 1, 2)
plt.plot(np.arange(len(result)), y_testRON, "bo-", label="True value 冲蚀速率")
plt.plot(np.arange(len(result)), resultRON, "ro-", label="Predict value 冲蚀速率")
plt.title(f"test_SVM---R^2:{score}")
plt.legend(loc="best")
plt.show()

##可视化标准误差
# test
RON = np.array(resultRON)
# train
RONtrain = np.array(resultRON_train)

RE_RONtest = abs(y_testRON - RON) / y_testRON

RE_RONtrain = abs(y_trainRON - RONtrain) / y_trainRON

plt.figure()
plt.plot(np.arange(len(RE_RONtrain)), RE_RONtrain, "ro-", label="RE value 冲蚀速率  -train")
plt.plot(np.arange(len(RE_RONtrain), len(RE_RONtrain) + len(RE_RONtest)), RE_RONtest, "bo-",
         label="RE value 冲蚀速率  -test")
plt.title('Relative Error')
plt.legend(loc="best")
plt.show()

PSO_SVR.py

import numpy as np
from sklearn.svm import SVR
from matplotlib import pyplot as plt
import pyswarms as ps

np.random.seed(42)


# 适应度函数
def fitness_function(params, X, y, xt, yt):
    C, gamma = params
    svm_model = SVR(kernel='rbf', gamma=gamma, C=C)
    svm_model.fit(X, y)
    y_pred = svm_model.predict(xt)
    mse = np.mean((yt - y_pred) ** 2)
    return mse


# 优化函数
def optimize_svm(X, y, xt, yt, n_particles=100, n_iterations=100):
    def _fitness_function(params):
        fitness_values = []
        for p in params:
            fitness = fitness_function(p, X, y, xt, yt)
            fitness_values.append(fitness)
        return fitness_values

    # 参数边界
    bounds = (np.array([0.1, 0.01]), np.array([50.0, 10.0]))
    options = {'c1': 0.5, 'c2': 0.3, 'w': 0.9}

    cost_history = np.zeros(n_iterations)
    # 运行优化器进行参数优化
    optimizer = ps.single.GlobalBestPSO(n_particles=n_particles, dimensions=2, bounds=bounds, options=options)

    best_cost, best_params = optimizer.optimize(_fitness_function, iters=n_iterations)

    # 在每次迭代前保存代价值
    for i, cost in enumerate(optimizer.cost_history):
        cost_history[i] = cost


    # 根据优化结果建立最终的SVM模型
    C, gamma = best_params
    svm_model = SVR(kernel='rbf', gamma=gamma, C=C)
    svm_model.fit(X, y)
    print('最优参数：', best_params)
    # 绘制代价值变化曲线
    plt.plot(range(n_iterations), cost_history)
    plt.xlabel('Iteration')
    plt.ylabel('Cost')
    plt.title('Cost Function Evolution')
    plt.show()

    return svm_model