堆排序详细解读

 

简介

堆排序是一种基于二叉堆数据结构的排序算法，它的特点是不同于传统的比较排序算法，它是通过建立一个堆结构来实现的。堆排序分为两个阶段，首先建立堆，然后逐步将堆顶元素与堆的最后一个元素交换并调整堆，使得最大（或最小）元素逐步沉到堆的末尾，完成排序。

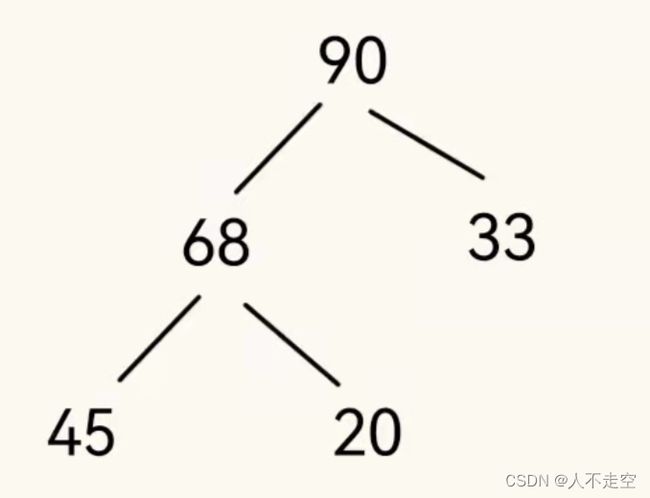
堆的概念

• 堆是一种特殊的树状数据结构，其中每个节点的值大于等于（或小于等于）其子节点的值。是一个平衡二叉树。
• 最大堆：每个节点的值都大于或等于其子节点的值。
• 
• 最小堆：每个节点的值都小于或等于其子节点的值。

堆排序步骤

1. 构建堆： 将待排序的数组构建成一个二叉堆。

   • 最大堆构建： 从数组的中间位置开始，从右至左，从下至上进行堆调整。
   • 最小堆构建： 从数组的中间位置开始，从右至左，从下至上进行堆调整。

2. 堆排序： 通过反复将堆的根节点（最大或最小值）与堆的最后一个元素交换，并重新调整堆，实现排序。

   • 最大堆排序： 将堆顶元素与堆的最后一个元素交换，然后将堆的大小减1，并重新调整堆。
   • 最小堆排序： 类似于最大堆排序，但是每次选择堆中的最小元素。

堆排序的代码示例（最大堆排序）

public class HeapSort {
    public static void main(String[] args) {
        int[] arr = {3, 8, 2, 5, 1, 4, 7, 6};
        heapSort(arr);
        for (int i : arr) {
            System.out.print(i + " ");
        }
    }

    public static void heapSort(int[] arr) {

        for (int i = (arr.length -1)/ 2 ; i >= 0; i--) {
            adjustHeap(arr, i, arr.length);
        }
        int temp;
        for (int j = arr.length - 1; j > 0; j--) {
            temp = arr[j];
            arr[j] = arr[0];
            arr[0] = temp;
            adjustHeap(arr, 0, j);
        }
    }

    public static void adjustHeap(int[] arr, int i, int length) {
        int 父节点 = arr[i];
        for (int k = i * 2 + 1; k < length; k = k * 2 + 1) {
            if (k + 1 < length && arr[k] < arr[k + 1]) {
                k++;
            }
            //k左右孩子较大的一个
            if (arr[k] > 父节点) {
                arr[i] = arr[k];
                i = k;
            } else {
                break;
            }
        }
        arr[i] = 父节点;
    }
    
    
}

 

 详细讲解

这段代码实现了堆排序（Heap Sort）算法。我将为你逐段解释代码的功能。

1. 初始化数组:

int[] arr = {3, 8, 2, 5, 1, 4, 7, 6};

这行代码定义了一个整数数组 arr，并初始化了8个数值。
2. 调用堆排序方法: 

heapSort(arr);

 这行代码调用了 heapSort 方法，并将数组 arr 作为参数传递。
3. 打印排序后的数组:

for (int i : arr) {  
    System.out.print(i + " ");  
}

这段代码遍历数组 arr 并打印每个元素。此时，数组应该已经被排序，所以输出的应该是排序后的数组：1 2 3 4 5 6 7 8 。
4. 堆排序方法:
堆排序方法分为两个主要部分：建立最大堆和交换堆顶元素与最后一个元素，然后调整堆。 

* **建立最大堆**:  
```  
java`for (int i = (arr.length -1)/ 2 ; i >= 0; i--) {  
    adjustHeap(arr, i, arr.length);  
}`  
```  
这段循环遍历数组的索引，从 `(arr.length -1)/ 2` 到 0，并对每个索引调用 `adjustHeap` 方法来调整堆。  
* **交换和调整堆**:  
```  
java`for (int j = arr.length - 1; j > 0; j--) {  
    temp = arr[j];  
    arr[j] = arr[0];  
    arr[0] = temp;  
    adjustHeap(arr, 0, j);  
}`  
```  
这段循环每次从数组的末尾开始，将堆顶元素（最大值）与最后一个元素交换，然后重新调整堆。这样，最大的元素会逐渐移到数组的末尾。

5. 调整堆方法:
这个方法负责调整堆以满足最大堆的特性。如果父节点的值小于其子节点的值，那么就需要交换它们。这个方法会一直递归地检查和调整，直到满足最大堆的条件为止。

6.主类HeapSort：这是整个程序的容器，它包含 main 方法和其他辅助方法。

好的，我继续为您解释这段代码。

7.adjustHeap方法详解:

public static void adjustHeap(int[] arr, int i, int length) {  
    int 父节点 = arr[i]; // 获取当前节点的值，并将其称为父节点  
    for (int k = i * 2 + 1; k < length; k = k * 2 + 1) { // 循环遍历左孩子节点，右孩子节点  
        if (k + 1 < length && arr[k] < arr[k + 1]) { // 如果右孩子的值大于左孩子的值  
            k++; // 则将k移动到右孩子的位置  
        }  
        //k左右孩子较大的一个  
        if (arr[k] > 父节点) { // 如果当前节点大于父节点  
            arr[i] = arr[k]; // 用当前节点的值替换父节点的值  
            i = k; // 将i设置为当前节点的索引  
        } else {  
            break; // 如果当前节点不大于父节点，则跳出循环  
        }  
    }  
    arr[i] = 父节点; // 将父节点的值设置回父节点位置  
}

这段代码的主要目的是确保堆的属性在调用该方法后得到满足。它从给定的索引 i 开始，并确保该索引下的子节点是最大的。如果子节点的值小于父节点，则交换它们。这个过程会继续，直到满足堆的属性为止。

总结：这段代码实现了一个堆排序算法。它首先构建一个最大堆，然后通过交换堆顶元素与最后一个元素来排序数组。每次交换后，它都会重新调整堆以确保其属性得到满足。