C语言实例:创建各类三角形图案(杨辉三角,弗洛伊德三角形....)
目录
1.正/倒直角三角形
2.金字塔
3.杨辉三角
4.弗洛伊德三角形
1.正/倒直角三角形
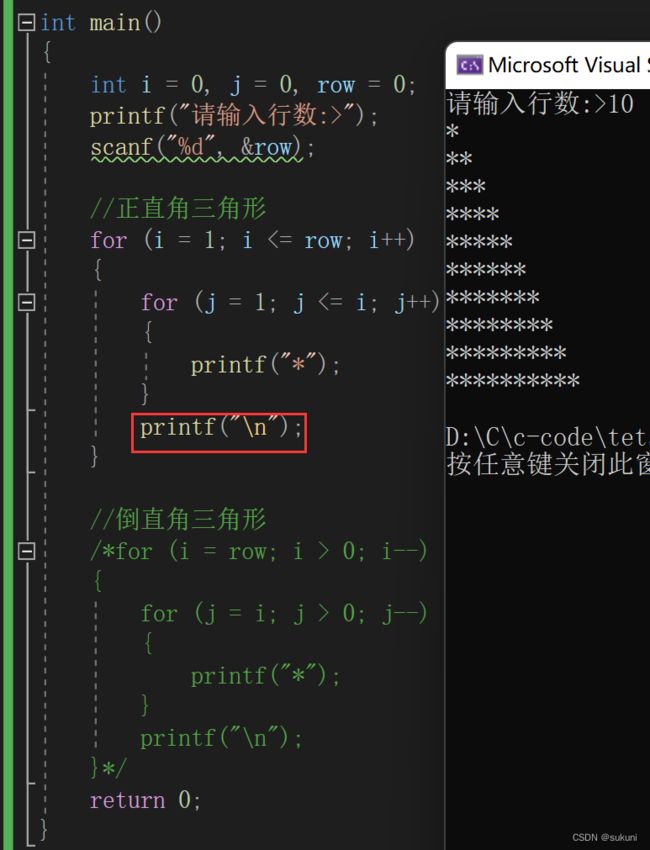
这种三角形的实现很简单,这里就不作过多的赘述了,直接看代码吧
红框里的代码很重要,没有这句话,三角形就打印不出来,打印的只是许多连起来的‘*’。
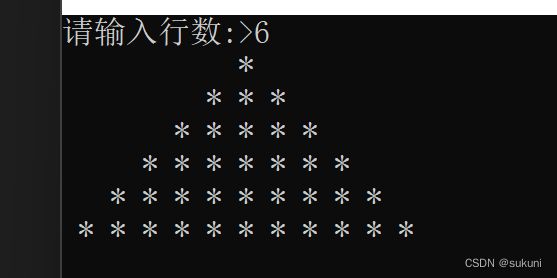
2.金字塔
可以看见金字塔由空格和星号组成。再仔细观察,不难发现空格的和星号的排列方式存在着规律。
第一行有1个星号,5个空格;第二行有3个星号,4个空格;第三行有5个星号,3个空格;
以此类推,那么第五行就有(2*5-1)个星号,0个空格。那么这个规律就可以通过循环实现
下面来看代码:
int main()
{
int i = 0, j = 0, row = 0,space=0;
printf("请输入行数:>");
scanf("%d", &row);
for (i = 0; i < row; i++)
{
//打印空格
for (space = 1; space < row - i; space++)
{
printf(" "); //注意空格的大小应与下方打印*所占的大小一致,否则打印出来的金字塔不好看
}
//打印星号
for (j = 1; j <= (2*(i+1) - 1); j++)
{
printf(" *");
}
printf("\n"); //换行很重要
}
return 0;
}打印出来的效果:
3.杨辉三角
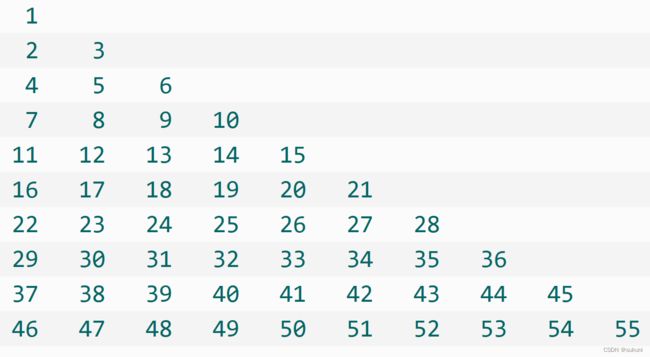
先来看看杨辉三角的特征:
每行的开始和末尾都是1,每个数等于它上方两数之和。每行数字左右对称,由1开始逐渐变大,第n行的数字有n项。有了这些特征,我们就能够写出代码:
int main()
{
int rows, coef = 1, space, i, j;
printf("行数: ");
scanf("%d", &rows);
for (i = 0; i < rows; i++)
{
//打印空格
for (space = 1; space <= rows - i; space++)
printf(" ");
for (j = 0; j <= i; j++)
{
if (j == 0 || i == 0)
coef = 1;
else
coef = coef * (i - j + 1) / j; //计算每行除1以外的数
printf("%4d", coef);
}
printf("\n");
}
return 0;
}看上去计算coef那以行的代码不好理解,没关系我们可以采用另一种方法。我们曾经在高中数学肯定了解过杨辉三角,知道它每一行的数其实是它当前的行数-1的组合数,这样一来就简单许多了,我们只需要写一个计算组合数的函数,然后调用它就行了 。
对组合数不理解的可以参考这篇文章:https://zhidao.baidu.com/question/1179242945073797019.html
下面是计算组合数的函数:
int Gulid(int n, int m)
{
int i = 0, ret1 = 1, ret2 = 1,tmp=0;
for (i = n;tmp我们把代码改成这样:
int main()
{
int i = 0, j = 0, space = 0, row = 0;
printf("请输入行数:>");
scanf("%d", &row);
for (i = 0; i < row; i++)
{
for (space = 1; space <= row - i; space++)
printf(" ");
for (j = 0; j <= i; j++)
{
printf("%4d", Gulid(i, j));
}
printf("\n");
}
return 0;
}这相比上面的就容易理解了许多
4.弗洛伊德三角形
弗洛伊德三角形就是每行有行数个数字,且打印的数字是递增的,如下图:
可以发现结尾的数字是从1到行数的和,1行就以1结尾,2行就是3,3行就是6......10行就是55;
我们可以写个函数来实现这个功能:
int Sum(int n)
{
int i = 0, sum = 0; //这里的sum=0很重要,否则算出来的答案就是错误的
for (i = 1; i <= n; i++)
{
sum = sum + i;
}
return sum;
}主函数:
int main()
{
int i = 0, j = 1,row=0,n=1,tmp=0,count=1;
printf("请输入行数:>");
scanf("%d", &row);
int sum = Sum(row); //计算结尾的数字
for (i = 1; i <= sum; i++)
{
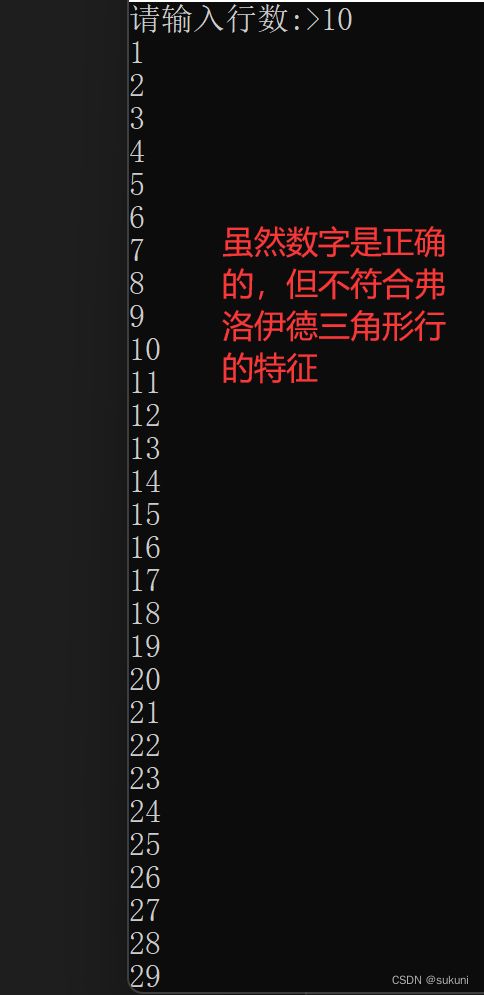
count = 1; //每次循环好一遍后,使count=1,否则会出现下图所示的结果
for (; count<= n; j++)
{
printf("%d ", j);
count++;
}
i = j; //让i=j,否则会得不到想要的结果,反而会得到一个出乎意料的结果
printf("\n");
n++; //记录行的变化
}
return 0;
}出乎意料的结果:
总结:对于我们想要创建或是打印的图形,需要好好观察,得出图形的特征,再用代码实现,而不是一上来就写代码。
好了,本篇文章就到这儿啦,谢谢你的阅读。
如有错误或意见,欢迎指出。