POJ 1397 The Bulk
这还是以前在spoj上A的一道题,不过直接在poj提交时Time Limit Exceeded,本打算有时间把算法重新优化一下,昨天无聊把输入改为scanf试试,没想到竟然过了,意料之外。
简单的讲一下思路:
我们先考虑平面求面积的情况:
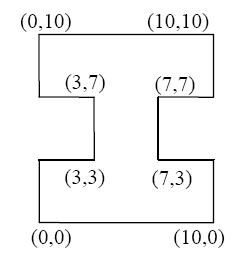
图1
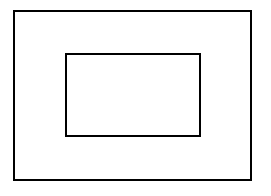
图2
考虑与x轴平行的线段,沿y轴从下往上
1)出现重叠就删除重叠部分
2)出现相接部分就连接起来
例 图1
首先出现线段(0,0)-(10,0),长度l=10,往上遇到(0,3)-(3,3)、(7,3)-(10,3),相对高度h=3,此时面积增加 Δs=l*h=30;
按照原理1)此时线段变为(3,3)-(7,3), l=4
往上遇到(0,7)-(3,7)、(7,7)-(10,7),相对高度h=4,此时面积增加 Δs=l*h=16;
按照原理2)此时线段变为(0,7)-(10,7),l=10
往上遇到(0,10)-(10,10),相对高度h=3,此时面积增加 Δs=l*h=30;
按照原理1)此时线段变为(0,0)-(0,0),结束
所以总面积为30+16+30=76
同理 图2(点坐标与图1相同)
s=10*3+(3+3)*4+10*3=84
按照这样的思路,我们可以扩展到三维情况求体积
代码比较烂,也懒得改了,仅供有需要者测试用
 代码
代码
#include
<
iostream
>
#include
<
fstream
>
#include
<
stdlib.h
>
using
namespace
std;
struct
ParallelXLine
{
int
X1;
int
X2;
int
Y;
int
Z;
}LineArray[
20000
], ZPlaneLine[
10000
], ZPlaneLineTemp[
10000
];
struct
C2DLine{
int
X1;
int
X2;
}curLineArray[
10000
], nextLineArray[
10000
];
struct
point{
int
X;
int
Y;
int
Z;
}PArray[
250
];
int
cmp(
const
void
*
a,
const
void
*
b)
{
struct
ParallelXLine
*
c
=
(ParallelXLine
*
)a;
struct
ParallelXLine
*
d
=
(ParallelXLine
*
)b;
if
(c
->
Z
!=
d
->
Z)
return
c
->
Z
-
d
->
Z;
if
(c
->
Y
!=
d
->
Y)
return
c
->
Y
-
d
->
Y;
if
(c
->
X1
!=
d
->
X1)
return
c
->
X1
-
d
->
X1;
else
return
c
->
X2
-
d
->
X2;
}
int
cmp2(
const
void
*
a,
const
void
*
b)
{
struct
ParallelXLine
*
c
=
(ParallelXLine
*
)a;
struct
ParallelXLine
*
d
=
(ParallelXLine
*
)b;
if
(c
->
Y
!=
d
->
Y)
return
c
->
Y
-
d
->
Y;
if
(c
->
X1
!=
d
->
X1)
return
c
->
X1
-
d
->
X1;
else
return
c
->
X2
-
d
->
X2;
}
int
main()
{
int
T, F, P, L, Index, CurZ, CurY, ZPL, ZPLT, CLA, NLA, CurLength;
int
area, vol;
scanf(
"
%d
"
,
&
T);
while
(T
--
)
{
scanf(
"
%d
"
,
&
F);
//
cin >> F;
L
=
0
;
while
(F
--
)
{
area
=
vol
=
0
;
//
cin >> P;
scanf(
"
%d
"
,
&
P);
bool
isParallelToXY;
int
pIndex;
for
(pIndex
=
0
, isParallelToXY
=
true
; pIndex
<
P; pIndex
++
)
{
scanf(
"
%d%d%d
"
,
&
PArray[pIndex].X,
&
PArray[pIndex].Y,
&
PArray[pIndex].Z);
if
(pIndex
>
0
&&
PArray[pIndex].Z
!=
PArray[pIndex
-
1
].Z)
isParallelToXY
=
false
;
}
if
(isParallelToXY)
{
for
(
int
i
=
0
; i
<
pIndex; i
++
)
{
if
(i
!=
0
&&
PArray[i].Y
==
PArray[i
-
1
].Y)
{
LineArray[L].X1
=
min(PArray[i].X, PArray[i
-
1
].X);
LineArray[L].X2
=
max(PArray[i].X, PArray[i
-
1
].X);
LineArray[L].Y
=
PArray[i].Y;
LineArray[L].Z
=
PArray[i].Z;
L
++
;
}
if
(i
==
P
-
1
&&
PArray[i].Y
==
PArray[
0
].Y)
{
LineArray[L].X1
=
min(PArray[i].X, PArray[
0
].X);
LineArray[L].X2
=
max(PArray[i].X, PArray[
0
].X);
LineArray[L].Y
=
PArray[i].Y;
LineArray[L].Z
=
PArray[i].Z;
L
++
;
}
if
(L
>
1
&&
LineArray[L
-
2
].Y
==
LineArray[L
-
1
].Y
&&
LineArray[L
-
2
].Z
==
LineArray[L
-
1
].Z)
{
if
(LineArray[L
-
2
].X2
==
LineArray [L
-
1
].X1)
{
LineArray[L
-
2
].X2
=
LineArray[L
-
1
].X2;
L
--
;
}
else
if
(LineArray[L
-
2
].X1
==
LineArray[L
-
1
].X2)
{
LineArray[L
-
2
].X1
=
LineArray[L
-
1
].X1;
L
--
;
}
}
}
}
}
qsort(LineArray, L,
sizeof
(LineArray[
0
]), cmp);
Index
=
0
;
ZPL
=
0
;
while
(Index
<
L)
{
if
(T
==
683
)
{
int
aa
=
0
;
}
if
(Index
!=
0
)
vol
+=
area
*
(LineArray[Index].Z
-
LineArray[Index
-
1
].Z);
CurZ
=
LineArray[Index].Z;
area
=
0
;
memcpy(ZPlaneLineTemp, ZPlaneLine, ZPL
*
sizeof
(ZPlaneLine[
0
]));
ZPLT
=
ZPL;
while
(Index
<
L
&&
LineArray[Index].Z
==
CurZ)
{
for
(CurY
=
LineArray[Index].Y; Index
<
L
&&
LineArray[Index].Y
==
CurY
&&
LineArray[Index].Z
==
CurZ; Index
++
)
{
if
(ZPLT
>
0
&&
LineArray[Index].X1
>=
ZPlaneLineTemp[ZPLT
-
1
].X1
&&
LineArray[Index].X1
<=
ZPlaneLineTemp[ZPLT
-
1
].X2
&&
LineArray[Index].Y
==
ZPlaneLineTemp[ZPLT
-
1
].Y
&&
LineArray[Index].Z
==
ZPlaneLineTemp[ZPLT
-
1
].Z)
{
if
(LineArray[Index].X1
>
ZPlaneLineTemp[ZPLT
-
1
].X1
&&
LineArray[Index].X1
<
ZPlaneLineTemp[ZPLT
-
1
].X2)
{
int
minX2
=
min(ZPlaneLineTemp[ZPLT
-
1
].X2, LineArray[Index].X2);
int
maxX2
=
max(ZPlaneLineTemp[ZPLT
-
1
].X2, LineArray[Index].X2);
ZPlaneLineTemp[ZPLT
-
1
].X2
=
LineArray[Index].X1;
if
(minX2
<
maxX2)
{
ZPlaneLineTemp[ZPLT].X1
=
minX2;
ZPlaneLineTemp[ZPLT].X2
=
maxX2;
ZPlaneLineTemp[ZPLT].Y
=
CurY;
ZPlaneLineTemp[ZPLT].Z
=
CurZ;
ZPLT
++
;
}
}
else
if
(LineArray[Index].X1
==
ZPlaneLineTemp[ZPLT
-
1
].X1)
{
int
minX2
=
min(ZPlaneLineTemp[ZPLT
-
1
].X2, LineArray[Index].X2);
int
maxX2
=
max(ZPlaneLineTemp[ZPLT
-
1
].X2, LineArray[Index].X2);
if
(minX2
<
maxX2)
{
ZPlaneLineTemp[ZPLT
-
1
].X1
=
minX2;
ZPlaneLineTemp[ZPLT
-
1
].X2
=
maxX2;
}
else
ZPLT
--
;
}
else
ZPlaneLineTemp[ZPLT
-
1
].X2
=
LineArray[Index].X2;
}
else
{
ZPlaneLineTemp[ZPLT].X1
=
LineArray[Index].X1;
ZPlaneLineTemp[ZPLT].X2
=
LineArray[Index].X2;
ZPlaneLineTemp[ZPLT].Y
=
LineArray[Index].Y;
ZPlaneLineTemp[ZPLT].Z
=
LineArray[Index].Z;
ZPLT
++
;
}
}
}
qsort(ZPlaneLineTemp, ZPLT,
sizeof
(ZPlaneLineTemp[
0
]), cmp2);
ZPL
=
0
;
NLA
=
0
;
for
(
int
i
=
0
; i
<
ZPLT;area
+=
(CurLength
*
(ZPlaneLineTemp[i].Y
-
ZPlaneLineTemp[i
-
1
].Y)))
{
int
split;
for
(CurY
=
ZPlaneLineTemp[i].Y, split
=
ZPL; i
<
ZPLT
&&
ZPlaneLineTemp[i].Y
==
CurY;)
{
if
(i
+
1
<
ZPLT
&&
ZPlaneLineTemp[i
+
1
].Y
==
CurY)
{
if
(ZPlaneLineTemp[i].X1
==
ZPlaneLineTemp[i
+
1
].X1)
{
if
(ZPlaneLineTemp[i].X2
==
ZPlaneLineTemp[i
+
1
].X2)
i
+=
2
;
else
{
ZPlaneLineTemp[i
+
1
].X1
=
ZPlaneLineTemp[i].X2;
i
++
;
}
}
else
if
(ZPlaneLineTemp[i].X2
==
ZPlaneLineTemp[i
+
1
].X1)
{
ZPlaneLineTemp[i
+
1
].X1
=
ZPlaneLineTemp[i].X1;
i
++
;
}
else
if
(ZPlaneLineTemp[i
+
1
].X1
>
ZPlaneLineTemp[i].X1
&&
ZPlaneLineTemp[i
+
1
].X1
<
ZPlaneLineTemp[i].X2)
{
ZPlaneLine[ZPL].X1
=
ZPlaneLineTemp[i].X1;
ZPlaneLine[ZPL].X2
=
ZPlaneLineTemp[i
+
1
].X1;
ZPlaneLine[ZPL].Y
=
CurY;
ZPlaneLine[ZPL].Z
=
ZPlaneLineTemp[i].Z;
ZPL
++
;
if
(ZPlaneLineTemp[i].X2
==
ZPlaneLineTemp[i
+
1
].X2)
i
+=
2
;
else
{
ZPlaneLineTemp[i
+
1
].X1
=
min(ZPlaneLineTemp[i
+
1
].X2, ZPlaneLineTemp[i].X2);
ZPlaneLineTemp[i
+
1
].X2
=
max(ZPlaneLineTemp[i
+
1
].X2, ZPlaneLineTemp[i].X2);
i
++
;
}
}
else
{
ZPlaneLine[ZPL].X1
=
ZPlaneLineTemp[i].X1;
ZPlaneLine[ZPL].X2
=
ZPlaneLineTemp[i].X2;
ZPlaneLine[ZPL].Y
=
CurY;
ZPlaneLine[ZPL].Z
=
ZPlaneLineTemp[i].Z;
i
++
;
ZPL
++
;
}
}
else
{
ZPlaneLine[ZPL].X1
=
ZPlaneLineTemp[i].X1;
ZPlaneLine[ZPL].X2
=
ZPlaneLineTemp[i].X2;
ZPlaneLine[ZPL].Y
=
CurY;
ZPlaneLine[ZPL].Z
=
ZPlaneLineTemp[i].Z;
i
++
;
ZPL
++
;
}
}
int
NLAIndex
=
0
;
CLA
=
0
;
CurLength
=
0
;
while
(split
<
ZPL
&&
NLAIndex
<
NLA)
{
if
(ZPlaneLine[split].X1
==
nextLineArray[NLAIndex].X1)
{
int
minX2
=
min(nextLineArray[NLAIndex].X2, ZPlaneLine[split].X2);
int
maxX2
=
max(nextLineArray[NLAIndex].X2, ZPlaneLine[split].X2);
if
(minX2
==
maxX2)
NLAIndex
++
;
else
{
nextLineArray[NLAIndex].X1
=
minX2;
nextLineArray[NLAIndex].X2
=
maxX2;
}
split
++
;
}
else
if
(ZPlaneLine[split].X2
==
nextLineArray[NLAIndex].X1)
{
nextLineArray[NLAIndex].X1
=
ZPlaneLine[split].X1;
split
++
;
}
else
if
(ZPlaneLine[split].X1
==
nextLineArray[NLAIndex].X2)
{
nextLineArray[NLAIndex].X2
=
ZPlaneLine[split].X2;
split
++
;
if
(NLAIndex
+
1
<
NLA
&&
nextLineArray[NLAIndex].X2
==
nextLineArray[NLAIndex
+
1
].X1)
{
nextLineArray[NLAIndex
+
1
].X1
=
nextLineArray[NLAIndex].X1;
NLAIndex
++
;
}
else
{
curLineArray[CLA].X1
=
nextLineArray[NLAIndex].X1;
curLineArray[CLA].X2
=
nextLineArray[NLAIndex].X2;
CurLength
+=
(curLineArray[CLA].X2
-
curLineArray[CLA].X1);
CLA
++
;
NLAIndex
++
;
}
}
else
if
(ZPlaneLine[split].X1
>
nextLineArray[NLAIndex].X2)
{
curLineArray[CLA].X1
=
nextLineArray[NLAIndex].X1;
curLineArray[CLA].X2
=
nextLineArray[NLAIndex].X2;
CurLength
+=
(curLineArray[CLA].X2
-
curLineArray[CLA].X1);
NLAIndex
++
;
CLA
++
;
}
else
if
(nextLineArray[NLAIndex].X1
>
ZPlaneLine[split].X2)
{
curLineArray[CLA].X1
=
ZPlaneLine[split].X1;
curLineArray[CLA].X2
=
ZPlaneLine[split].X2;
CurLength
+=
(curLineArray[CLA].X2
-
curLineArray[CLA].X1);
CLA
++
;
split
++
;
}
else
{
curLineArray[CLA].X1
=
min(nextLineArray[NLAIndex].X1, ZPlaneLine[split].X1);
curLineArray[CLA].X2
=
max(nextLineArray[NLAIndex].X1, ZPlaneLine[split].X1);
CurLength
+=
(curLineArray[CLA].X2
-
curLineArray[CLA].X1);
CLA
++
;
int
minX2
=
min(nextLineArray[NLAIndex].X2, ZPlaneLine[split].X2);
int
maxX2
=
max(nextLineArray[NLAIndex].X2, ZPlaneLine[split].X2);
if
(minX2
==
maxX2)
NLAIndex
++
;
else
{
nextLineArray[NLAIndex].X1
=
minX2;
nextLineArray[NLAIndex].X2
=
maxX2;
}
split
++
;
}
}
while
(split
<
ZPL)
{
curLineArray[CLA].X1
=
ZPlaneLine[split].X1;
curLineArray[CLA].X2
=
ZPlaneLine[split].X2;
CurLength
+=
(curLineArray[CLA].X2
-
curLineArray[CLA].X1);
CLA
++
;
split
++
;
}
while
(NLAIndex
<
NLA)
{
curLineArray[CLA].X1
=
nextLineArray[NLAIndex].X1;
curLineArray[CLA].X2
=
nextLineArray[NLAIndex].X2;
CurLength
+=
(curLineArray[CLA].X2
-
curLineArray[CLA].X1);
CLA
++
;
NLAIndex
++
;
}
memcpy(nextLineArray, curLineArray, CLA
*
sizeof
(curLineArray[
0
]));
NLA
=
CLA;
}
}
printf(
"
The bulk is composed of %d units.\n
"
, vol);
}
return
0
;
}
