探索数据之美：优雅权重计算方法与Python实践

写在开头

在数据的世界里，我们常常需要通过各种方法为不同的数据点分配合理的权重。这是数据分析中至关重要的一环，它决定了模型的准确性和结果的可信度。本文将引导您探索数据分析中常用的权重计算方法，并通过清晰的Python代码实现，让您轻松驾驭权重的奥秘。

1.常见分类

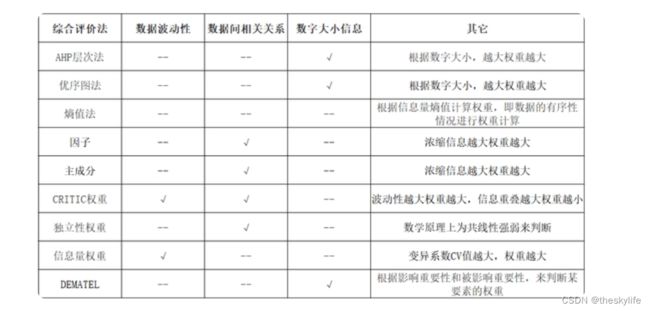
2.区别

权重信息评价：

2.1第一类为AHP层次法和优序图法；

此类方法利用数字的相对大小信息进行权重计算；此类方法为主观赋值法，通常需要由专家打分或通过问卷调研的方式，得到各指标重要性的打分情况，得分越高，指标权重越大。

此类方法适合于多种领域。比如想构建一个员工绩效评价体系，指标包括工作态度、学习能力、工作能力、团队协作。通过专家打分计算权重，得到每个指标的权重，并代入员工数据，即可得到每个员工的综合得分情况。

2.2 第二类为熵值法（熵权法）

此类方法利用数据熵值信息即信息量大小进行权重计算。此类方法适用于数据之间有波动，同时会将数据波动作为一种信息的方法。

比如收集各地区的某年份的经济指标数据，包括产品销售率（X1）、资金利润率（X2）、成本费用利润率（X3）、劳动生产率（X4）、流动资金周转次数（X5），用熵值法计算出各指标权重，再对各地区经济效益进行比较。

2.3 第三类为CRITIC、独立性权重和信息量权重；

此类方法主要是利用数据的波动性或者数据之间的相关关系情况进行权重计算。

比如研究利用某省医院2011年共计5个科室的数据指标（共计6个指标数据）进行CRITIC权重计算，最终可得到出院人数、入出院诊断符合率、治疗有效率、平均床位使用率、病床周转次数、出院者平均住院日这6个指标的权重。如果希望针对各个科室进行计算综合得分，那么可以直接将权重与自身的数据进行相乘累加即可，分值越高代表该科室评价越高。

2.4 第四类为因子分析和主成分法；

此类方法利用了数据的信息浓缩原理，利用方差解释率进行权重计算。

比如对30个地区的经济发展情况的8项指标作主成分分析，主成分分析法可以将8个指标浓缩为几个综合指标（主成分），用这些指标（主成分）反映原来指标的信息，同时利用方差解释率得出各个主成分的权重。

3. 使用时注意事项

4.详细描述及python中实现方法

以python3.10环境为例。

4.1 AHP层次法

4.1.1 计算过程

AHP（层次分析法，Analytic Hierarchy Process）是一种用于解决复杂决策问题、确定多层次结构中各因素的相对权重的方法。该方法通过构建判断矩阵、计算权重向量，层次分解和一致性检验等步骤，最终得到各因素的权重。

AHP计算权重的基本过程：

1). 构建层次结构：

• 将问题分解为若干层次，包括目标层、准则层和子准则层。每个层次上的因素称为因子。

2). 构建判断矩阵：

• 对于每个层次中的两两因子，专家根据其相对重要性给出判断矩阵。判断矩阵通常用 $A$ 表示，其元素 $a_{ij}$ 表示因子 $i$ 相对于因子 $j$ 的相对重要性。

3). 计算权重向量：

• 对于每个判断矩阵，计算其最大特征值 ${\lambda }_{\max }$ 和对应的特征向量 $\mathbf{v}$。
• 归一化特征向量，得到权重向量 $\mathbf{w}$。权重向量的每个元素表示对应因子的权重。
• 对于判断矩阵 $A$，其权重向量为 $\mathbf{w}$，满足 $A\cdot \mathbf{w}={\lambda }_{\max }\cdot \mathbf{w}$。

4). 层次分解：

• 将权重向量按照层次结构逐级进行分解，得到最终的全局权重。

5). 一致性检验：

• 对于每个判断矩阵，计算一致性指标 $CI$。如果 $CI$ 大于某个阈值（通常为0.1），则需要进行一致性调整。一致性指标 $CI$ 的计算公式为：$CI=\frac{{\lambda }_{\max }-n}{n-1}$，其中 $n$ 是判断矩阵的阶数。
• 一致性比 $CR$ 可用于进一步检验一致性，计算公式为 $CR=\frac{CI}{RI}$，其中 $RI$ 是随机一致性指标，根据矩阵的阶数查表获得。

以上是AHP权重计算的基本过程和数学公式。在实际应用中，通常使用计算工具来进行繁琐的计算。

4.1.2 Python代码实现

import numpy as np

def ahp_weight(matrix):
    eigvals, eigvecs = np.linalg.eig(matrix)
    weights = eigvecs[:, np.argmax(eigvals)]
    normalized_weights = weights / sum(weights)
    return normalized_weights

4.1.3 应用场景

假设我们在选择投资标的时，需要考虑收益、风险和流动性三个因素。我们可以通过AHP方法计算权重。

# 构建判断矩阵
matrix = np.array([[1, 2, 3],
                   [1/2, 1, 2],
                   [1/3, 1/2, 1]])

# 计算权重
weights = ahp_weight(matrix)
print("权重分配结果:", weights)

4.2. 优序图法（Ranking Method）

4.2.1 计算过程

优序图法（Analytic Hierarchy Process，AHP）是一种用于计算多指标系统中各指标权重的方法。该方法基于对比矩阵，通过构建判断矩阵，计算一致性指标，进行层次分解和一致性检验等步骤，最终得到各指标的权重。

优序图法计算权重的基本过程：

1). 构建层次结构：

• 将多指标系统分解为若干层次，形成层次结构。通常包括目标层、准则层和方案层。

2). 构建判断矩阵：

• 对每个层次中的两两元素进行比较，形成判断矩阵。对于准则层和方案层，可以采用专家判断、实验数据或其他方法进行比较。
• 判断矩阵通常用 $A$ 表示，其元素 $a_{ij}$ 表示元素 $i$ 相对于元素 $j$ 的重要性。

3). 一致性检验：

• 计算一致性指标 $CI$。如果 $CI$ 大于某个阈值（通常为0.1），则需要进行一致性调整。
• 一致性指标的计算公式为：$CI=\frac{{\lambda }_{\max }-n}{n-1}$
  其中，${\lambda }_{\max }$ 是判断矩阵的最大特征值，$n$ 是判断矩阵的阶数。

4). 一致性调整：

• 通过随机一致性指标 $RI$ 和一致性比 $CR$ 对判断矩阵进行一致性调整。
• 一致性比的计算公式为：$CR=\frac{CI}{RI}$
  如果 $CR$ 大于某个阈值（通常为0.1），则需要重新进行专家判断或者修改判断矩阵。

5). 计算权重：

• 根据一致性通过的判断矩阵，计算权重向量 $W$。
• 权重向量的计算通常涉及最大特征值法或特征向量法。

通过这个计算过程，优序图法能够为每个层次中的元素分配一个权重，该权重反映了各元素在整体层次结构中的相对重要性。

4.2.2 Python代码实现

import networkx as nx

def ranking_weight(graph):
    ranks = nx.pagerank(graph)
    weights = [ranks[node] for node in graph.nodes]
    normalized_weights = weights / sum(weights)
    return normalized_weights

4.2.3 应用场景

考虑在选择供应商时，我们需要综合考虑价格、质量和交货时间三个因素。我们可以通过优序图法计算权重。

# 构建优序图
G = nx.DiGraph()
G.add_weighted_edges_from([("价格", "质量", 0.6), ("价格", "交货时间", 0.8), ("质量", "交货时间", 0.7)])

# 计算权重
weights = ranking_weight(G)
print("权重分配结果:", weights)

4.3. 熵值法（Entropy Method）

4.3.1 计算过程

熵值法是一种用于计算多指标系统中各指标权重的方法，该方法基于信息熵的概念。它通过分析各指标的信息熵来确定它们的权重，从而反映了指标的不确定性和贡献度。

熵值法计算权重的基本过程：

1). 构建指标矩阵：

• 将多指标系统的数据构建成一个矩阵 $X$，其中每一行对应一个样本，每一列对应一个指标。

2). 归一化处理：

• 对指标矩阵 $X$ 进行归一化处理，将各指标的取值范围映射到[0, 1] 区间。这可以通过线性变换等方法进行。

3). 计算熵值：

• 对每个指标进行熵值的计算。熵值 $E_i$ 的计算公式为：$E_i=-\frac{1}{\ln (n)}{\sum }_{j=1}^n{p}_{ij}\ln (p_{ij})$
  其中，$p_{ij}$ 是指标 $X_i$ 在第 $j$ 个样本上的相对权重，$n$ 是样本数。

4). 计算权重：

• 计算每个指标的权重 $W_i$。权重的计算公式为： W i = 1 − E i ∑