高级搜索——伸展树Splay详解

伸展树Splay

对于二叉搜索树的平衡性我们有很多的处理方式，AVL树中引入平衡因子，红黑树中引入颜色，Treap中引入堆的性质，今天要介绍的Splay最为特殊，其利用了局部性原理，实现了每次访问达到均摊O(logn)的时间复杂度。

伸展树Splay的定义

伸展树(splay tree) ，也是平衡二叉搜索树的一种形式，但并非严格的平衡。但是其实现相较于AVL树和红黑树更为简捷。伸展树无需时刻都严格地保持全树的平衡，但却能够在任何足够长的真实操作序列中，保持分摊意义上的高效率。伸展树也不需要对基本的二叉树节点结构，做任何附加的要求或改动，更不需要记录平衡因子或高度之类的额外信息，故适用范围更广。

局部性原理

局部性（locality）可以分为时间局部性（temporal locality）和空间局部性（spatial locality）。

假如你在书桌旁工作，需要查阅某本书籍，便将书架上的书拿过来，查阅后又放回书架，但是你发现你着手的工作需要频繁地查阅这本书，于是你将书放到了书桌上，因为很快你就要再次查阅。这就是时间局部性的体现。

当你找到一本关于EDSAC的早期经典计算机的书籍时，也许紧挨着它的另一本关于早期工业计算机的书籍里同样有你所需的材料，这也是为什么图书馆通常将主题相同的书放在同一个书架.上以提高空间定位效率。这就是空间局部性的体现。

于是我们对局部性原理有如下理解：

1)刚刚被访问过的元素，极有可能在不久之后再次被访问到
2)将被访问的下一元素，极有可能就处于不久之前被访问过的某个元素的附近

充分利用好此类特性，即可进一步地提高数据结构和算法的效率。

那么对于我们的二叉搜索树而言，局部性就体现为：

1)刚刚被访问过的节点，极有可能在不久之后再次被访问到
2)将被访问的下一节点，极有可能就处于不久之前被访问过的某个节点的附近

D.DSleator和R.E.Tarjan于1985年发现只需将刚被访问的节点，及时地“转移”至树根(附近)，即可加速后续的操作，在此基础上对二叉搜索树进行优化，并命名为伸展树（Splay）。

Splay的伸展操作

前面提到了，Splay利用局部性原理，遵循对于访问过的节点将其转移到根节点，保证了均摊效率。那么显然，实现一种操作，能够将某节点移动到根节点，这个关键操作也是我们Splay的名称的由来，伸展（splay）。

逐层伸展

我们AVL树、红黑树、Treap调整平衡性的共同操作都是旋转(Treap也有无旋式实现方式)，我们实现伸展的第一个选择就是利用旋转将其逐层旋转到根节点。

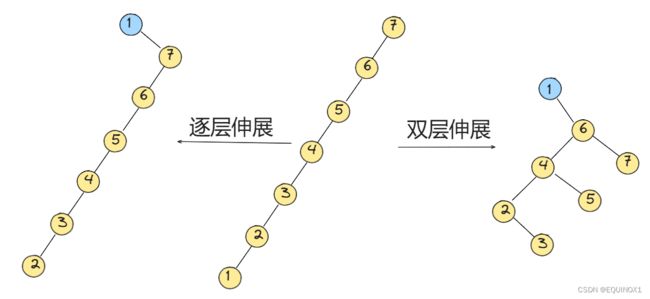
我们以下图为例，通过两次右单旋和一次左单旋将E节点旋转到了根节点的位置。

随着节点E的逐层上升，两侧子树的结构也不断地调整，故这一过程也形象地称作伸展(splay)，而采用这一调整策略的二叉搜索树也因此得名。不过，为实现真正意义上的伸展树，还须对以上策略做点微妙而本质的改进。之所以必须改进，是因为目前的策略仍存在致命
的缺陷一-对于很多访问序列，单次访问的分摊时间复杂度在极端情况下可能高达O(n)。

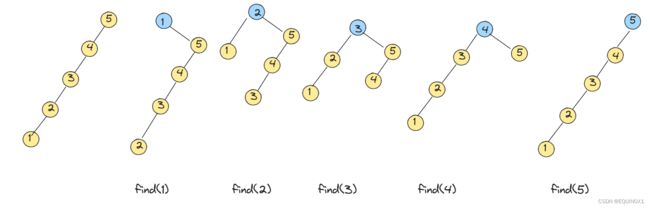
即然上面的示例过于理想，我们不妨来试试最坏情况下的伸展，如左下图中左倾斜的序列{1，2，3，4，5}，我们假设已经实现了查找操作find，每次find都会把查找的节点放到根节点，我们不妨依次查找1，2，3，4，5

可见，在各次访问之后，为将对应节点伸展调整至树根，分别需做4、4、3、2和1次旋转。

如果在一般情况下，节点总数为n，旋转的总次数就是(n - 1) + (n-1) + (n-2) + … + 1 = (n^2 + n - 2) / 2 = O(n^2)

如此以来，n次查找的均摊时间复杂度就是O(n)，这相比于最坏情况下的二叉搜索树毫无优势。更糟糕的是，上图中5次查找后，树的结构又复原了！也就是说我们上述情况还会重复。

实际上，上述特例可以推广到规模任意的简易伸展树，如果按照关键字的大小顺序查找，我们每次访问的均摊时间复杂度都是O(n)！

那么这类最坏情况是否可以回避？如何回避？

双层伸展

当我们将单层伸展改为双层伸展后，上述问题就迎刃而解。

即然我们要经过若干次旋转将节点旋转到根的位置，那么我们就使其每次旋转两次（追溯两层），如果其父节点为根，则旋转一次（追溯一层）。

前导英语储备zig(右旋)zag(左旋)

我们的旋转分为三种类型

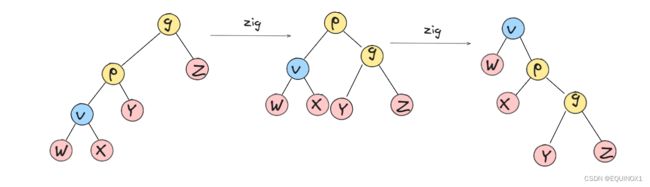
zig-zig/zag-zag

可见zig-zig/zag-zag就是两次右/左单旋

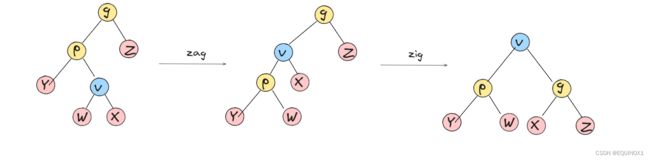
zig-zag/zag-zig

可见zig-zag/zag-zig就是右左/左右双旋

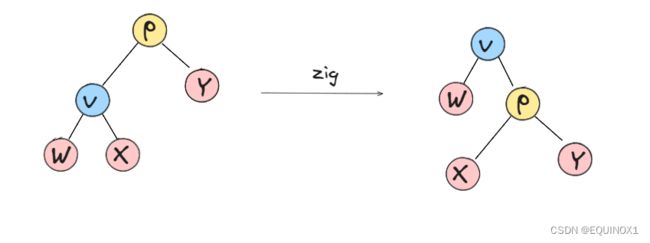
zig/zag

可见zig/zag就是单次次右/左单旋

双层伸展的效果与效率

由上面的各种情况， 不难发现每经过一次伸展操作 节点v都会上升两层，如果v的初始深度为偶数，那么最终v将上升至树根，如果depth为奇数，那么当v上升至树根时的孩子时，只需执行单次旋转即可。

那么在双层伸展下，我们上面的最坏情况又会是怎样的结果呢？

我们仍以单倾斜的二叉搜索树为例，我们发现执行单次的search(1)操作，二者的结果产生了很大差别

可见，最深节点(1)被访问之后再经过双层调整，不仅同样可将该节点伸展至树根，而且同时可使树的高度接近于减半。就树的形态而言，双层伸展策略可“智能”地“折叠”被访问的子树分支，从而有效地避免对长分支的连续访问。这就意味着，即便节点v的深度为O(n)，双层伸展策略既可将v推至树根，亦可令对应分支的长度以几何级数(大致折半)的速度收缩。

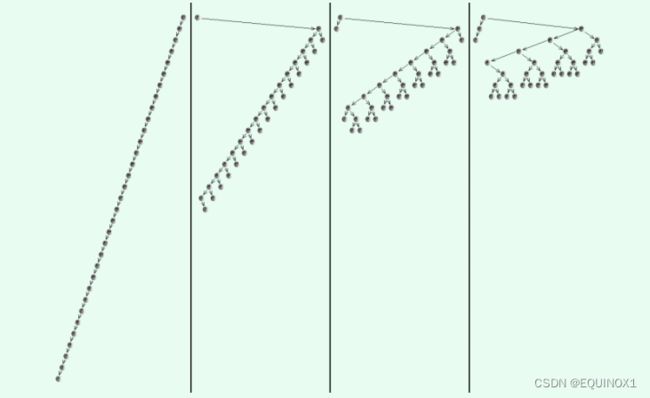
下图则展现出了节点更多，更具一般性的样例，展现出了双层伸展的效果。

尽管伸展树不像AVL树和红黑树那么严格，随时都有可能出现很深的节点，但是一旦该节点被访问，那么就会像含羞草似的，经过双层伸展，其分支都会收缩至长度大致减半。于是，即便每次都“恶意地”试图访问最底层节点，最坏情况也不会持续发生。可见，伸展树虽不能杜绝最坏情况的发生，却能有效地控制最坏情况发生的频度，从而在分摊意义下保证整体的高效率。

伸展树的实现

伸展树的实现逻辑非常简单，就是在基础二叉搜索树的操作上，对于操作中访问的节点将其Splay到根节点的位置，不过具体实现上还是由些微差别的。

实现方式无非就是动态和静态两种方式，静态版本由于逻辑简单和代码简洁性而在OJ题目中广泛应用。

动态版本实现

递增分配器

关于递增分配器的作用，在[高级搜索-线段树C/C++]-CSDN博客已经有所介绍，其实就是一个用来充当缓存的链表，我们如果每次开节点都要new一个出来的话效率太低，所以我们可以提前开一部分出来，然后用的时候拿出来即可，这里不再过多赘述。

// 递增分配器
template 
class CacheObj
{
public:
    void *operator new(size_t)
    {
        if (!_head)
        {
            T *a = new T[SIZE];
            for (size_t i = 0; i < SIZE; i++)
                add(a + i);
        }
        T *ret = _head;
        _head = _head->CacheObj::_next;
        return ret;
    }
    void operator delete(void *p, size_t)
    {
        if (p)
            add(static_cast(p));
    }
    virtual ~CacheObj() {}

protected:
    T *_next;

private:
    static T *_head;
    static const size_t SIZE;
    static void add(T *p)
    {
        p->CacheObj::_next = _head;
        _head = p;
    }
};
template 
T *CacheObj::_head = nullptr;
template 
const size_t CacheObj::SIZE = 10000;

节点定义

动态版本的我们先不对权值进行扩展，只是先实现一棵基本的Splay，所以节点定义和普通的二叉搜索树相同。

class Node : public CacheObj
{
public:
    Node(int v = 0) : _v(v), _left(nullptr), _right(nullptr), _parent(nullptr)
    {
    }
    int _v;
    Node *_left;
    Node *_right;
    Node *_parent;
};

Splay类及其接口定义

    class Splay
    {
    public:
        Splay() : _root(nullptr) {}
        Node *splay(Node *p, Node *parent = nullptr)//伸展
        {}；
        Node *search(int x)//查找
        {}；
        Node *insert(int x)//插入
        {}；
        bool erase(int x)//删除
        {}；
    public:
        Node *_root;
    };

伸展操作

伸展操作就是判断三种情况然后调用对应的旋转，旋转的实现是二叉搜索树中最基础的，如需详解，可见[AVL树详解C++]-CSDN博客

左单旋

    void RotateL(Node *parent)
    {
        Node *SubR = parent->_right;
        Node *SubRL = SubR->_left;
        Node *ppNode = parent->_parent;

        parent->_right = SubRL;
        if (SubRL)
            SubRL->_parent = parent;
        SubR->_left = parent;
        parent->_parent = SubR;

        if (_root == parent)
        {
            _root = SubR;
        }
        else
        {
            if (ppNode->_left == parent)
                ppNode->_left = SubR;
            else
                ppNode->_right = SubR;
        }
        SubR->_parent = ppNode;
    }

右单旋

    void RotateR(Node *parent)
    {
        Node *SubL = parent->_left;
        Node *SubLR = SubL->_right;
        Node *ppNode = parent->_parent;

        parent->_left = SubLR;
        if (SubLR)
            SubLR->_parent = parent;
        SubL->_right = parent;
        parent->_parent = SubL;

        if (_root == parent)
        {
            _root = SubL;
        }
        else
        {
            if (ppNode->_left == parent)
                ppNode->_left = SubL;
            else
                ppNode->_right = SubL;
        }
        SubL->_parent = ppNode;
    }

右左/左右双旋

    void RotateRL(Node *root)
    {
        RotateR(root->_right);
        RotateL(root);
    }
    void RotateLR(Node *root)
    {
        RotateL(root->_left);
        RotateR(root);
    }

伸展

对于伸展接口定义如下splay(Node *p, Node *parent = nullptr)，意为将节点p伸展到parent下面，当parent为空自然是伸展至根节点

操作流程：

• 获取节点p的父节点pNode和祖父节点ppNode
• 根据三种情况执行对应的旋转
• 当p的父节点为parent时，伸展结束
• 返回p节点

    Node *splay(Node *p, Node *parent = nullptr)
    {
        if (!p)
            return p;
        while (p->_parent != parent)
        {
            Node *pNode = p->_parent;
            Node *ppNode = pNode->_parent;
            if (ppNode != parent)
            {
                if (ppNode->_left == pNode)
                {
                    if (pNode->_left == p)
                        RotateR(ppNode);
                    else
                    {
                        RotateLR(ppNode);
                        continue;
                    }
                }
                else if (ppNode->_right == pNode && pNode->_right == p)
                {
                    if (pNode->_right == p)
                        RotateL(ppNode);
                    else
                    {
                        RotateRL(ppNode);
                        continue;
                    }
                }
            }
            if (pNode->_left == p)
                RotateR(pNode);
            else
                RotateL(pNode);
        }
        return p;
    }

查找操作

按照二叉搜索树的查找规则去找对应键值的节点，找到就返回，否则返回前驱节点，对于返回节点要执行伸展操作来保证均摊时间复杂度。

操作流程：

• 待查找结点键值x
• 节点cur用于遍历，pre用于保存前驱节点（注意，pre键值可能小于x也可能大于x）
• cur键值等于x，说明找到，break
• cur键值小于x就往右走，大于x就往左走
• 对最终的返回节点进行伸展操作（保证均摊时间复杂度的关键）

    Node *find(int x)
    {
        Node *cur = _root, *pre = nullptr;
        while (cur)
        {
            pre = cur;
            if (cur->_v == x)
                break;
            else if (cur->_v > x)
                cur = cur->_left;
            else
                cur = cur->_right;
        }
        return splay(cur ? cur : pre);
    }

删除操作

像AVL树和红黑树的删除操作可以说是十分繁琐，而对于我们的Splay来讲，却没有这般烦恼。

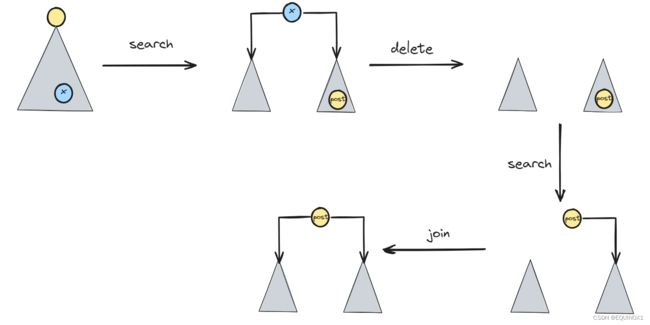
对于二叉搜索树的删除操作的策略都是替换删除法，Splay也不例外，我们可以按照二叉搜索树删除模式，删除后对其后继节点进行伸展，但是我们的Splay操作可以直接将待删除结点提升到根节点的位置，所以我们可以采用另一种策略来进行删除。

对于待删除关键字x，我们用search查询x，不妨假设找到了且其左右孩子不为空，那么我们将左子树断开，删除关键字结点，并将其右孩子作为根，再次查找x，这次会查找失败但是会将x结点的后继结点提升到根，这时再将左子树重新连接，我们就又得到了一棵Splay。

操作流程：

• 待删除关键字x，查找x
• 查找失败返回false，成功则保存结点为del
• 左为空，将右孩子作为根，右为空，左孩子作为根
• 左右都不为空，断开左子树，右孩子作为根，再次查找x，再将左子树连接
• 删除待删除结点del，返回true

        bool erase(int x)
        {
            if (!_root || search(x)->_v != x)
                return false;
            Node *del = _root;
            if (!_root->_left)
            {
                _root = _root->_right;
                if (_root)
                    _root->_parent = nullptr;
            }
            else if (!_root->_right)
            {
                _root = _root->_left;
                if (_root)
                    _root->_parent = nullptr;
            }
            else
            {
                Node *SubL = _root->_left;
                SubL->_parent = _root->_left = nullptr;
                _root = _root->_right;
                _root->_parent = nullptr;
                search(del->_v);
                _root->_left = SubL;
                SubL->_parent = _root;
            }
            delete del;
            return true;
        }

插入操作

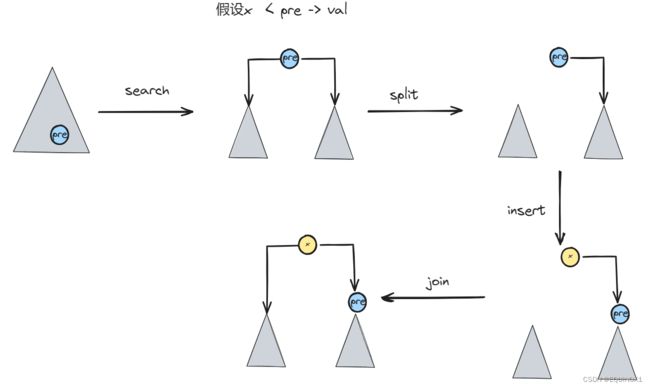
插入操作同样利用了splay()伸展功能，对于待插入关键字x，查找返回后，树根节点要么等于查找目标(查找成功)，要么就是拟插入节点的直接前驱或直接后继(查找失败)。因此，不妨改用如下方法实现插入功能。

为将关键字x插至伸展树T中，首先调用查找接口search(x)，于是，其中最后被访问的节点pre，将通过伸展被提升为树根。
根据k与pre存储关键字的大小关系(不妨排除二者相等的情况)，以pre为界将整棵树分裂为两棵子树。按照大小关系将pre插入到x的左节点或者右节点即可然后更新根节点为x（局部性原理）。

操作流程：

• 待插入关键字x，查找x
• 查找成功返回_root，成功则保存结点为pre
• 根更新为关键字为x的新结点
• pre->_v > x，则pre为_root右孩子，pre的左给root，同时维护pre的左孩子父节点为root（如果pre的左孩子非空）
• pre->_v < x，则pre为_root左孩子，pre的右给root，同时维护pre的右孩子父节点为root（如果pre的右孩子非空）
• 返回_root

        Node *insert(int x)
        {
            if (!_root)
            {
                return _root = new Node(x);
            }

            Node *pre = search(x);
            if (pre->_v == x)
                return _root;

            if (pre->_v > x)
            {
                pre->_parent = _root = new Node(x, pre->_left, pre);
                if (pre->_left)
                    pre->_left->_parent = _root;
                pre->_left = nullptr;
            }
            else if (pre->_v < x)
            {
                pre->_parent = _root = new Node(x, pre, pre->_right);
                if (pre->_right)
                    pre->_right->_parent = _root;
                pre->_right = nullptr;
            }
            return _root;
        }

完整代码

namespace D_Splay
{
    // 递增分配器
    template 
    class CacheObj
    {
    public:
        void *operator new(size_t)
        {
            if (!_head)
            {
                T *a = new T[SIZE];
                for (size_t i = 0; i < SIZE; i++)
                    add(a + i);
            }
            T *ret = _head;
            _head = _head->CacheObj::_next;
            return ret;
        }
        void operator delete(void *p, size_t)
        {
            if (p)
                add(static_cast(p));
        }
        virtual ~CacheObj() {}

    protected:
        T *_next;

    private:
        static T *_head;
        static const size_t SIZE;
        static void add(T *p)
        {
            p->CacheObj::_next = _head;
            _head = p;
        }
    };
    template 
    T *CacheObj::_head = nullptr;
    template 
    const size_t CacheObj::SIZE = 10000;
    class Node : public CacheObj
    {
    public:
        Node(int v = 0, Node *left = nullptr, Node *right = nullptr) : _v(v), _left(left), _right(right), _parent(nullptr)
        {
        }
        int _v;
        Node *_left;
        Node *_right;
        Node *_parent;
    };
    class Splay
    {
    public:
        Splay() : _root(nullptr) {}
        Node *splay(Node *p, Node *parent = nullptr)
        {
            if (!p)
                return p;
            while (p->_parent != parent)
            {
                Node *pNode = p->_parent;
                Node *ppNode = pNode->_parent;
                if (ppNode != parent)
                {
                    if (ppNode->_left == pNode)
                    {
                        if (pNode->_left == p)
                            RotateR(ppNode);
                        else
                        {
                            RotateLR(ppNode);
                            continue;
                        }
                    }
                    else if (ppNode->_right == pNode && pNode->_right == p)
                    {
                        if (pNode->_right == p)
                            RotateL(ppNode);
                        else
                        {
                            RotateRL(ppNode);
                            continue;
                        }
                    }
                }
                if (pNode->_left == p)
                    RotateR(pNode);
                else
                    RotateL(pNode);
            }
            return p;
        }
        Node *search(int x)
        {
            Node *cur = _root, *pre = nullptr;
            while (cur)
            {
                pre = cur;
                if (cur->_v == x)
                    break;
                else if (cur->_v > x)
                    cur = cur->_left;
                else
                    cur = cur->_right;
            }
            return splay(cur ? cur : pre);
        }
        Node *insert(int x)
        {
            if (!_root)
            {
                return _root = new Node(x);
            }

            Node *pre = search(x);
            if (pre->_v == x)
                return _root;

            if (pre->_v > x)
            {
                pre->_parent = _root = new Node(x, pre->_left, pre);
                if (pre->_left)
                    pre->_left->_parent = _root;
                pre->_left = nullptr;
            }
            else if (pre->_v < x)
            {
                pre->_parent = _root = new Node(x, pre, pre->_right);
                if (pre->_right)
                    pre->_right->_parent = _root;
                pre->_right = nullptr;
            }
            return _root;
        }
        bool erase(int x)
        {
            if (!_root || search(x)->_v != x)
                return false;
            Node *del = _root;
            if (!_root->_left)
            {
                _root = _root->_right;
                if (_root)
                    _root->_parent = nullptr;
            }
            else if (!_root->_right)
            {
                _root = _root->_left;
                if (_root)
                    _root->_parent = nullptr;
            }
            else
            {
                Node *SubL = _root->_left;
                SubL->_parent = _root->_left = nullptr;
                _root = _root->_right;
                _root->_parent = nullptr;
                search(del->_v);
                _root->_left = SubL;
                SubL->_parent = _root;
            }
            delete del;
            return true;
        }
        void Inorder()
        {
            _InOrder(_root);
        }

    private:
        void _InOrder(Node *root)
        {
            if (!root)
                return;
            _InOrder(root->_left);
            cout << root->_v << " ";
            _InOrder(root->_right);
        }
        void RotateL(Node *parent)
        {
            Node *SubR = parent->_right;
            Node *SubRL = SubR->_left;
            Node *ppNode = parent->_parent;

            parent->_right = SubRL;
            if (SubRL)
                SubRL->_parent = parent;
            SubR->_left = parent;
            parent->_parent = SubR;

            if (_root == parent)
            {
                _root = SubR;
            }
            else
            {
                if (ppNode->_left == parent)
                    ppNode->_left = SubR;
                else
                    ppNode->_right = SubR;
            }
            SubR->_parent = ppNode;
        }
        void RotateR(Node *parent)
        {
            Node *SubL = parent->_left;
            Node *SubLR = SubL->_right;
            Node *ppNode = parent->_parent;

            parent->_left = SubLR;
            if (SubLR)
                SubLR->_parent = parent;
            SubL->_right = parent;
            parent->_parent = SubL;

            if (_root == parent)
            {
                _root = SubL;
            }
            else
            {
                if (ppNode->_left == parent)
                    ppNode->_left = SubL;
                else
                    ppNode->_right = SubL;
            }
            SubL->_parent = ppNode;
        }
        void RotateRL(Node *root)
        {
            RotateR(root->_right);
            RotateL(root);
        }
        void RotateLR(Node *root)
        {
            RotateL(root->_left);
            RotateR(root);
        }

    public:
        Node *_root;
    };
}

静态版本实现

动态版本虽然实现逻辑简单，但是还是有一定的代码量的，我们这里来介绍以下代码更为简洁的静态版本。、

静态版本下我们实现很多操作会更为方便，于是像treap一样，我们对结点引入权值w代表当前结点的数目，size代表以当前结点为根的子树结点数目

结点定义

const int N = 1e5 + 10;
struct Node
{
    Node() = default;
    int _c[2]; // 孩子节点
    int _p;    // 父节点
    int _v;    // 值域
    int _w;    // 权值
    int _size; // 子树节点数目
    void init(int p, int v)
    {
        _p = p, _v = v;
        _w = _size = 1;
    }
} tr[N];
int root = 0, idx = 0;

接口定义

接口看起来很多，但实现起来其实十分简洁，特别是旋转操作我们由三个旋转简化为了一个旋转

void pushup(int x);//更新size
void rotate(int x);//旋转
void splay(int x, int p);
void find(int v);//查找
int get_pre(int v);//获得前驱
int get_suc(int v);//获得后继
void erase(int v);//删除
int get_rnk(int v);//获取排名
int get_val(int k);//获取第k小元素
void insert(int v);//插入
void Init();//初始化

rotate操作

静态版本的rotate是根据待旋转结点与父节点以及当前结点的位置关系来判断进行左旋还是右旋 ，由于静态版本结点都是通过下标索引，所以我们可以大大简化代码量，具体流程看代码注释。

void pushup(int x)
{
    tr[x]._size = tr[tr[x]._c[0]]._size + tr[tr[x]._c[1]]._size + tr[x]._w;
}
void rotate(int x)
{
    int y = tr[x]._p, z = tr[y]._p;//y为父结点下标，z为祖先结点下标
    int k = tr[y]._c[1] == x;//k为判断右孩子是否为x，是为1，否则为0
    tr[y]._c[k] = tr[x]._c[k ^ 1];//k为1就把x的左孩子给y的右孩子，否则把x的右孩子给y的左孩子
    tr[tr[x]._c[k ^ 1]]._p = y;//把y的新孩子的父节点置为y
    tr[x]._c[k ^ 1] = y;//y置为x的孩子
    tr[y]._p = x;//y的父节点置为x
    tr[z]._c[tr[z]._c[1] == y] = x;//根据z和y的关系来更新z的新孩子
    tr[x]._p = z;//更新x的父节点
    pushup(y), pushup(x);//更新x和y的size
}

splay操作

我们的双层伸展也变得十分简单

操作流程：

• 待伸展结点x伸展到p下面
• y为x父节点，z为祖先结点
• z不为p，则说明要进行双层伸展，根据直线型或者是折线型决定第一次旋转x还是y
• 旋转x
• x的父结点为p就退出循环

void splay(int x, int p)
{
    while (tr[x]._p != p)
    {
        int y = tr[x]._p, z = tr[y]._p;
        if (p != z)
        {
            (tr[y]._c[0] == x) ^ (tr[z]._c[0] == y) ? rotate(x) : rotate(y);
        }
        rotate(x);
    }
    if (!p)
        root = x;
}

find操作

同样是BST的查找结点流程，只不过静态版本的更为简洁，同样的，没找到v我们就返回最后一个不为空的结点

注意：这里while循环条件严格意义上其实是不对的，但是由于我们插入了-1e9和1e9两个哨兵结点保证了树不为空所以是对的，后面的init有讲

void find(int v)
{
    int x = root;
    while (tr[x]._c[tr[x]._v < v] && v != tr[x]._v)
        x = tr[x]._c[tr[x]._v < v];
    // 没找到时返回v的前驱或后继
    splay(x, 0);
}

get_pre操作

同样由于我们插入了-1e9和1e9两个哨兵结点保证了树不为空所以是对的

操作流程：

• 查找v，如果此时查找返回结点被提升到根
• 根的关键字小于v就返回根
• 否则返回根左子树的最右结点，返回前进行伸展操作

int get_pre(int v)
{
    find(v); // v在根或者其前驱或后继在根
    int x = root;
    if (tr[x]._v < v)
        return x;
    x = tr[x]._c[0];
    while (tr[x]._c[1])
        x = tr[x]._c[1];
    splay(x, 0);
    return x;
}

get_suc操作

和获得前驱类似的流程，同样由于我们插入了-1e9和1e9两个哨兵结点保证了树不为空所以是对的

操作流程：

• 查找v，如果此时查找返回结点被提升到根
• 根的关键字大于v就返回根
• 否则返回根右子树的最左结点，返回前进行伸展操作

int get_suc(int v)
{
    find(v);
    int x = root;
    if (tr[x]._v > v)
        return x;
    x = tr[x]._c[1];
    while (tr[x]._c[0])
        x = tr[x]._c[0];
    splay(x, 0);
    return x;
}

erase操作

erase的操作正确性的关键也基于我们插入了-1e9和1e9两个哨兵结点保证了树不为空，但是erase没有对待删除结点不在树里面进行特判！

• 操作流程
• 我们先获取前驱pre，再获取后继suc
• 将pre伸展到根，将suc伸展到pre下面
• 由于pre，v，suc三个结点为中序序列中连续的三个节点，所以此时位置关系为pre在根，suc在pre的右孩子，那么待删除v只能在pre的左孩子，所以我们删除pre的左孩子del
• 如果del权值大于1，那么权值-1同时splaydel
• 否则suc左孩子置空，伸展suc到根

void erase(int v)
{
    int pre = get_pre(v), suc = get_suc(v);
    splay(pre, 0), splay(suc, pre);
    int del = tr[suc]._c[0];
    if (tr[del]._w > 1)
        tr[del]._w--, splay(del, 0);
    else
        tr[suc]._c[0] = 0, splay(suc, 0);
}

get_rnk操作

注意我们树中-1e9和1e9两个哨兵的存在

查找v，此时v或者v的前驱或后继在根的位置，由于哨兵结点-1e9的存在，根结点左子树的size为根节点的排名

如果根小于v，左子树size为我们返回左子树size+1

否则根节点大于等于v，左子树size就是排名

int get_rnk(int v)
{
    find(v);
    return tr[root]._v < v ? tr[tr[root]._c[0]]._size + 1 : tr[tr[root]._c[0]]._size;
}

get_val操作

查找第k名元素，由于哨兵-1e9的存在，我们实际上要返回排名k + 1的结点

查找流程

• 查找排名k，遍历结点x，x的左孩子y
• 如果k + 2大于整棵树的结点数目我们就返回-1，否则k = k + 1
• 否则，如果x的权值和y的size和小于k，我们就往右子树查找k - tr[y]._size + tr[x]._w的元素
• 如果说左孩子y的size大于等于k，那么到左子树去找
• 否则x就是目标结点
• 将x伸展到根

int get_val(int k) // 获取第k名元素
{
    if (k + 2 > tr[root]._size)
        return -1;
    int x = root;
    ++k;
    while (1)
    {
        int y = tr[x]._c[0];
        if (tr[y]._size + tr[x]._w < k)
        {
            k -= tr[y]._size + tr[x]._w;
            x = tr[x]._c[1];
        }
        else
        {
            if (tr[y]._size >= k)
                x = y;
            else
                break;
        }
    }
    splay(x, 0);
    return tr[x]._v;
}

insert操作

我们按照BST的插入方式进行插入即可，结束时把新结点伸展到根

void insert(int v)
{
    int x = root, p = 0;
    while (x && tr[x]._v != v)
        p = x, x = tr[x]._c[tr[x]._v < v];
    if (x)
        tr[x]._w++;
    else
    {
        x = ++idx;
        tr[p]._c[tr[p]._v < v] = x;
        tr[x].init(p, v);
    }
    splay(x, 0);
}

init操作与哨兵结点的设置

初始化就是把idx和root置为0，tr数组置为0

为了减少各种操作对于空树的特判，我们选择插入两个哨兵结点，保证获取前驱后继都能找到，查找排名都能查到

void Init()
{
    idx = root = 0;
    memset(tr, 0, sizeof(tr));
    insert(-1e9), insert(1e9);
}

完整代码

#define int long long
const int N = 1e5 + 10;
struct Node
{
    Node() = default;
    int _c[2]; // 孩子节点
    int _p;    // 父节点
    int _v;    // 值域
    int _w;    // 权值
    int _size; // 子树节点数目
    void init(int p, int v)
    {
        _p = p, _v = v;
        _w = _size = 1;
    }
} tr[N];
int root = 0, idx = 0;
void pushup(int x)
{
    tr[x]._size = tr[tr[x]._c[0]]._size + tr[tr[x]._c[1]]._size + tr[x]._w;
}
void rotate(int x)
{
    int y = tr[x]._p, z = tr[y]._p;
    int k = tr[y]._c[1] == x;
    tr[y]._c[k] = tr[x]._c[k ^ 1];
    tr[tr[x]._c[k ^ 1]]._p = y;
    tr[x]._c[k ^ 1] = y;
    tr[y]._p = x;
    tr[z]._c[tr[z]._c[1] == y] = x;
    tr[x]._p = z;
    pushup(y), pushup(x);
}
void splay(int x, int p)
{
    while (tr[x]._p != p)
    {
        int y = tr[x]._p, z = tr[y]._p;
        if (p != z)
        {
            (tr[y]._c[0] == x) ^ (tr[z]._c[0] == y) ? rotate(x) : rotate(y);
        }
        rotate(x);
    }
    if (!p)
        root = x;
}
void find(int v)
{
    int x = root;
    while (tr[x]._c[tr[x]._v < v] && v != tr[x]._v)
        x = tr[x]._c[tr[x]._v < v];
    // 没找到时返回v的前驱或后继
    splay(x, 0);
}
int get_pre(int v)
{
    find(v); // v在根或者其前驱或后继在根
    int x = root;
    if (tr[x]._v < v)
        return x;
    x = tr[x]._c[0];
    while (tr[x]._c[1])
        x = tr[x]._c[1];
    splay(x, 0);
    return x;
}
int get_suc(int v)
{
    find(v);
    int x = root;
    if (tr[x]._v > v)
        return x;
    x = tr[x]._c[1];
    while (tr[x]._c[0])
        x = tr[x]._c[0];
    splay(x, 0);
    return x;
}
void erase(int v)
{
    int pre = get_pre(v), suc = get_suc(v);
    splay(pre, 0), splay(suc, pre);
    int del = tr[suc]._c[0];
    if (tr[del]._w > 1)
        tr[del]._w--, splay(del, 0);
    else
        tr[suc]._c[0] = 0, splay(suc, 0);
}
int get_rnk(int v)
{
    find(v);
    return tr[root]._v < v ? tr[tr[root]._c[0]]._size + 1 : tr[tr[root]._c[0]]._size;
}
int get_val(int k) // 获取第k名元素
{
    if (k + 2 > tr[root]._size)
        return -1;
    int x = root;
    ++k;
    while (1)
    {
        int y = tr[x]._c[0];
        if (tr[y]._size + tr[x]._w < k)
        {
            k -= tr[y]._size + tr[x]._w;
            x = tr[x]._c[1];
        }
        else
        {
            if (tr[y]._size >= k)
                x = y;
            else
                break;
        }
    }
    splay(x, 0);
    return tr[x]._v;
}
void insert(int v)
{
    int x = root, p = 0;
    while (x && tr[x]._v != v)
        p = x, x = tr[x]._c[tr[x]._v < v];
    if (x)
        tr[x]._w++;
    else
    {
        x = ++idx;
        tr[p]._c[tr[p]._v < v] = x;
        tr[x].init(p, v);
    }
    splay(x, 0);
}
void inorder(int x)
{
    if (!x)
        return;
    inorder(tr[x]._c[0]);
    cout << tr[x]._v << " ";
    inorder(tr[x]._c[1]);
}
void Init()
{
    idx = root = 0;
    memset(tr, 0, sizeof(tr));
    insert(-1e9), insert(1e9);
}

#include 
#include 
#include 
#include 
using namespace std;
#define int long long
const int N = 1e5 + 10;
struct Node
{
    Node() = default;
    int _c[2]; // 孩子节点
    int _p;    // 父节点
    int _v;    // 值域
    int _w;    // 权值
    int _size; // 子树节点数目
    void init(int p, int v)
    {
        _p = p, _v = v;
        _w = _size = 1;
    }
} tr[N];
int root = 0, idx = 0;
void pushup(int x)
{
    tr[x]._size = tr[tr[x]._c[0]]._size + tr[tr[x]._c[1]]._size + tr[x]._w;
}
void rotate(int x)
{
    int y = tr[x]._p, z = tr[y]._p;
    int k = tr[y]._c[1] == x;
    tr[y]._c[k] = tr[x]._c[k ^ 1];
    tr[tr[x]._c[k ^ 1]]._p = y;
    tr[x]._c[k ^ 1] = y;
    tr[y]._p = x;
    tr[z]._c[tr[z]._c[1] == y] = x;
    tr[x]._p = z;
    pushup(y), pushup(x);
}
void splay(int x, int p)
{
    while (tr[x]._p != p)
    {
        int y = tr[x]._p, z = tr[y]._p;
        if (p != z)
        {
            (tr[y]._c[0] == x) ^ (tr[z]._c[0] == y) ? rotate(x) : rotate(y);
        }
        rotate(x);
    }
    if (!p)
        root = x;
}
void find(int v)
{
    int x = root;
    while (tr[x]._c[tr[x]._v < v] && v != tr[x]._v)
        x = tr[x]._c[tr[x]._v < v];
    // 没找到时返回v的前驱或后继
    splay(x, 0);
}
int get_pre(int v)
{
    find(v); // v在根或者其前驱或后继在根
    int x = root;
    if (tr[x]._v < v)
        return x;
    x = tr[x]._c[0];
    while (tr[x]._c[1])
        x = tr[x]._c[1];
    splay(x, 0);
    return x;
}
int get_suc(int v)
{
    find(v);
    int x = root;
    if (tr[x]._v > v)
        return x;
    x = tr[x]._c[1];
    while (tr[x]._c[0])
        x = tr[x]._c[0];
    splay(x, 0);
    return x;
}
void erase(int v)
{
    int pre = get_pre(v), suc = get_suc(v);
    splay(pre, 0), splay(suc, pre);
    int del = tr[suc]._c[0];
    if (tr[del]._w > 1)
        tr[del]._w--, splay(del, 0);
    else
        tr[suc]._c[0] = 0, splay(suc, 0);
}
int get_rnk(int v)
{
    find(v);
    return tr[root]._v < v ? tr[tr[root]._c[0]]._size + 1 : tr[tr[root]._c[0]]._size;
}
int get_val(int k) // 获取第k名元素
{
    if (k + 2 > tr[root]._size)
        return -1;
    int x = root;
    ++k;
    while (1)
    {
        int y = tr[x]._c[0];
        if (tr[y]._size + tr[x]._w < k)
        {
            k -= tr[y]._size + tr[x]._w;
            x = tr[x]._c[1];
        }
        else
        {
            if (tr[y]._size >= k)
                x = y;
            else
                break;
        }
    }
    splay(x, 0);
    return tr[x]._v;
}
void insert(int v)
{
    int x = root, p = 0;
    while (x && tr[x]._v != v)
        p = x, x = tr[x]._c[tr[x]._v < v];
    if (x)
        tr[x]._w++;
    else
    {
        x = ++idx;
        tr[p]._c[tr[p]._v < v] = x;
        tr[x].init(p, v);
    }
    splay(x, 0);
}
void inorder(int x)
{
    if (!x)
        return;
    inorder(tr[x]._c[0]);
    cout << tr[x]._v << " ";
    inorder(tr[x]._c[1]);
}
void Init()
{
    idx = root = 0;
    memset(tr, 0, sizeof(tr));
    insert(-1e9), insert(1e9);
}
signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    Init();
    int n, opt, x;
    cin >> n;
    while (n--)
    {
        cin >> opt >> x;
        switch (opt)
        {
        case 1:
            insert(x);
            break;
        case 2:
            erase(x);
            break;
        case 3:
            cout << get_rnk(x) << '\n';
            break;
        case 4:
            cout << get_val(x) << '\n';
            break;
        case 5:
            cout << tr[get_pre(x)]._v << '\n';
            break;
        case 6:
            cout << tr[get_suc(x)]._v << '\n';
            break;
        default:
            break;
        }
    }
    return 0;
}

*伸展树的性能分析与证明

伸展树的单次操作的时间不同情况下差异很大，并不能始终保证在log(n)内，故需从平摊的角度来计算其时间复杂度，我们采用平摊分析法来分析，但是伸展树的性能分析更为复杂，故而采用算法平摊分析中的势能分析法（Potential Method）。

仿照物理学的思想和概念，这里可假想式地认为，每棵伸展树S都具有一定量(非负)的势能(potential) ，记作中Φ(S)。于是，若经过某- -操作并相应地通过旋转完成伸展之后S演化为另一伸展树S’，则对应的势能变化为:
$$\Delta \Phi =\Phi (S^{\prime })-\Phi (S)$$
那么对于一棵伸展树S0而言，连续进行m(m >> n)次操作的过程中，记第i次操作后的伸展树为Si，则有

$$\Delta \Phi =\Phi (Si)-\Phi (Si-1)，1<=i<=m$$
如果从整体来看就有
$$\Delta \Phi ={\sum }_{i=1}^m[\Phi (Si)-\Phi (Si-1)]=\Phi (Sm)-\Phi (S0)$$
也就是说，整体的势能变化量仅取决于最初和最终状态一这与物理学中势能场的规律吻合。势能函数与物理学中势能的另一相似之处在于，它也可以被看作是能量(计算成本)的一种存在形式。比如，当某一步计算实际所需的时间小于分摊复杂度时，则可理解为通过势能的增加将提前支出的计算成本存储起来;反之，在前者大于后者时，则可从此前积累的势能中支取相应量用于支付超出的计算成本。

我们记第i次操作的分摊复杂度为实际复杂度和势能变化量之和：
$$A=Ti+\Delta \Phi i$$
则
$${\sum }_{i=1}^{m}Ai={\sum }_{i=1}^{m}Ti+[\Phi (Sm)-\Phi (S0)]$$

$$这样一来，我们实际运行时间{\sum }_{i=1}^{m}Ti不会超过总体的分摊运行时间{\sum }_{i=1}^{m}Ai，所以后者是前者的上界$$
我们的算法界大牛R.E.Tarjan采用如下势能函数
$$\Phi (S)={\sum }_{v\in S}^{}log\left|v\right|，其中\left|v\right|=结点v的后代数目$$

证明了伸展树单次操作的分摊时间复杂度为O(logn)。为此，以下将分三种情况(其余情况不过是它们的对称形式)证明:

在对节点v的伸展过程中，每一步调整所需时间均不超过v的势能变化的3倍，即:3[Φ`(v) - Φ(v)]*

情况一：zig

该情况在双层伸展中最多出现一次，即最后一步伸展，所以这一步的实际复杂度T为O(1)，但是我们势能定义为后代数目，所以势能其实是变化了的，那么我们的分摊复杂度为：
$$A=T+\Delta \Phi =1+\Delta \Phi (p)+\Delta \Phi (v)=1+[{\Phi }^{\prime }(v)-\Phi (v)]$$
情况二：zig-zag

对于双旋而言，实际调整时间为 T= O(2)，而我们的pushdown操作也揭示了势能变化量，则有
$$\begin{array}{rl}A& =T+\Delta \Phi \\ & =2+\Delta \Phi (v)+\Delta \Phi (p)+\Delta \Phi (g)\\ & =2+{\Phi }^{\prime }(v)-\Phi (v)+{\Phi }^{\prime }(p)-\Phi (p)+{\Phi }^{\prime }(g)-\Phi (g)\\ & =2+{\Phi }^{\prime }(p)+{\Phi }^{\prime }(g)-\Phi (v)-\Phi (p)，({\Phi }^{\prime }(v)=\Phi (g)v伸展后的size和g初始size相同)\\ & <=2+{\Phi }^{\prime }(p)+{\Phi }^{\prime }(g)-2\ast \Phi (v)，(\Phi (v)<\Phi (p))\\ & <=2+2\ast {\Phi }^{\prime }(v)-2-2\ast \Phi (v)，({\Phi }^{\prime }(p)+{\Phi }^{\prime }(g)<=2\ast {\Phi }^{\prime }(v)-2)\\ & =2\ast [{\Phi }^{\prime }(v)-\Phi (v)]\end{array}$$
倒数第二行那里用了基本不等式，因为log为上凸函数，所以函数中值大于两点中值，(log2 a + log2 b) / 2<= log2 ((a + b) / 2)

log2 a + log2 b <= 2 * (log2 (a + b) / 2) = 2 * log2 (a + b) - 2 < 2 * log2 c - 2(c > a + b，也就对应v的size大于g，p的size之和)

情况三：zig-zig

和情况二证明类似，最后一步放缩即可
$$\begin{array}{rl}A& =T+\Delta \Phi \\ & =2+\Delta \Phi (v)+\Delta \Phi (p)+\Delta \Phi (g)\\ & =2+{\Phi }^{\prime }(v)-\Phi (v)+{\Phi }^{\prime }(p)-\Phi (p)+{\Phi }^{\prime }(g)-\Phi (g)\\ & =2+{\Phi }^{\prime }(p)+{\Phi }^{\prime }(g)-\Phi (v)-\Phi (p)，({\Phi }^{\prime }(v)=\Phi (g)v伸展后的size和g初始size相同)\\ & <=2+{\Phi }^{\prime }(p)+{\Phi }^{\prime }(g)-2\ast \Phi (v)，(\Phi (v)<\Phi (p))\\ & <=2+{\Phi }^{\prime }(g)+{\Phi }^{\prime }(v)-2\ast \Phi (v)，({\Phi }^{\prime }(p)<{\Phi }^{\prime }(v))\\ & <=3\ast [{\Phi }^{\prime }(v)-\Phi (v)],(最后一步放缩是用{\Phi }^{\prime }(g)+\Phi (v)<=2{\Phi }^{\prime }(v)-2)\end{array}$$
综上，我们伸展操作的每一步至多需要3*[Φ’[v] - Φ[v]]的时间，那么我们某次操作中，把一个结点v伸展到根r的分摊时间复杂度

A <= 1+ 3 * [Φ® - Φ(v)] <= 1 + 3 * Φ® = O(1 + logn) = O(logn)