单词的压缩编码（后缀树的使用）

说在前面

后缀树（suffix tree）是一种数据结构，通常用于字符串处理。后缀树可以快速找到一个字符串所有的子串，因此在文本搜索、字符串匹配等领域有广泛应用。

后缀树的构建过程是将一个字符串的所有后缀插入到一棵树中。这个树满足以下性质：

根节点代表空字符串。
每个非根节点都表示一个非空字符串的后缀。
从根节点到叶子节点的路径表示一个原始字符串的后缀。
由于每个节点都代表了一个字符串的后缀，因此可以在后缀树上很容易地查找一个字符串的所有子串，只需要找到以该字符串为前缀的所有路径即可。

构建后缀树的时间复杂度为O(n)，其中n是字符串的长度，因此后缀树是一种高效的字符串处理数据结构。

题目描述

单词数组 words 的 有效编码 由任意助记字符串 s 和下标数组 indices 组成，且满足：

words.length == indices.length
助记字符串 s 以 ‘#’ 字符结尾
对于每个下标 indices[i] ，s 的一个从 indices[i] 开始、到下一个 ‘#’ 字符结束（但不包括 ‘#’）的 子字符串 恰好与 words[i] 相等
给你一个单词数组 words ，返回成功对 words 进行编码的最小助记字符串 s 的长度 。

示例 1：

输入：words = ["time", "me", "bell"]
输出：10
解释：一组有效编码为 s = "time#bell#" 和 indices = [0, 2, 5] 。
words[0] = "time" ，s 开始于 indices[0] = 0 到下一个 '#' 结束的子字符串，如加粗部分所示 "time#bell#"
words[1] = "me" ，s 开始于 indices[1] = 2 到下一个 '#' 结束的子字符串，如加粗部分所示 "time#bell#"
words[2] = "bell" ，s 开始于 indices[2] = 5 到下一个 '#' 结束的子字符串，如加粗部分所示 "time#bell#"

示例 2：

输入：words = ["t"]
输出：2
解释：一组有效编码为 s = "t#" 和 indices = [0] 。

提示：

1 <= words.length <= 2000
1 <= words[i].length <= 7
words[i] 仅由小写字母组成

思路分析

通过题目描述我们可以知道这道题是需要我们将多个单词通过#号来辅助标识然后进行压缩。如s = "time#bell#" 和 indices = [0, 2, 5] 可以表示["time", "me", "bell"]这三个单词。
简单分析一下这个例子，我们可以发现’time’和’me’有相同的后缀’me’，所以可以将’time’和’me’结合起来，即’time’可以同时表示’time’和’me’这两个单词。所以这道题我们可以使用后缀树的思想来解题，后缀树的本质其实和前缀树是一样的，我们将单词翻转过来进行记录的前缀树就变成后缀树了，那么前缀树又是什么呢？

前缀树

前缀树又称单词查找树，Trie树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计，排序和保存大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希树高。
它有3个基本性质：根节点不包含字符，除根节点外每一个节点都只包含一个字符； 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串； 每个节点的所有子节点包含的字符都不相同。
前缀树本质就是一种树结构，每一个节点存放一个字母，并连接下一个字母，这样多个字母连接起来就是一个完整的单词了，如下图所示：

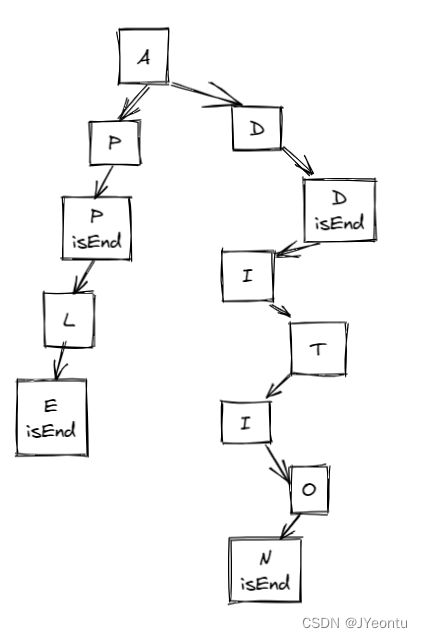
上图即为一个简单的字典树结构，图中总共包含4个单词，分别为app、apple、add、addition。将上图结构转为json格式数据如下。

{
  a:{
    p:{
      p:{
        isEnd: true
        l:{
          e:{
            isEnd:true
          }
        }
      }
    },
    d:{
      d:{
        isEnd:true,
        i:{
          t:{
            i:{
              o:{
                n:{
                  isEnd:true
                }
              }
            }
          }
        }
      }
    }
  }
}

javascript实现前缀树结构

/**
 * Initialize your data structure here.
 */
//声明结构体
var Trie = function() {
    this.tree = {};
};

/**
 * Inserts a word into the trie. 
 * @param {string} word
 * @return {void}
 */
//实现数据插入方法
Trie.prototype.insert = function(word) {
    let tree = this.tree;
    for(const w of word){
        if(tree[w] == undefined){
            tree[w] = {};
        }
        tree = tree[w];
    }
    tree.isEnd = true;
};

/**
 * Returns if the word is in the trie. 
 * @param {string} word
 * @return {boolean}
 */
//数据检索方法
Trie.prototype.search = function(word) {
    let tree = this.tree;
    for(const w of word){
        if(tree[w] == undefined){
            return false;
        }
        tree = tree[w];
    }
    return tree.isEnd == true;
};

/**
 * Returns if there is any word in the trie that starts with the given prefix. 
 * @param {string} prefix
 * @return {boolean}
 */
//检索是否存在该前缀组成的单词
Trie.prototype.startsWith = function(prefix) {
    let tree = this.tree;
    for(const w of prefix){
        if(tree[w] == undefined){
            return false;
        }
        tree = tree[w];
    }
    return true;
};

/**
 * Your Trie object will be instantiated and called as such:
 * var obj = new Trie()
 * obj.insert(word)
 * var param_2 = obj.search(word)
 * var param_3 = obj.startsWith(prefix)
 */

AC代码

回归到本题目中来，我们可以这样做：

• 定义后缀树类
  insert 方法中在每个单词的结尾加上一个属性wordLen来记录该单词的完整长度。
  getNum 方法是为题目编写的一个方法，计算最少需要的字符数。

class trimTree{
    constructor(){
        this.tree = {};
    };
    insert(word){
        let tree = this.tree;
        let wordLen = 0;
        for(let i = word.length - 1; i >= 0; i--){
            const w = word[i];
            !tree[w] ? tree[w] = {} : '';
            tree = tree[w];
            wordLen++;
        }
        tree.isStart = true;
        tree.wordLen = wordLen;
    };
    getNum(t = this.tree,num = 0){
        if(!t) return;
        for(let k in t){
            if(k === 'wordLen' && Object.keys(t).length == 2){
                num += t[k] + 1;
            }else if(k !== 'isStart') num += this.getNum(t[k]);
        }
        return num;
    }
}

• 构建后缀树

const tree = new trimTree();
for(const word of words){
    tree.insert(word);
}

完整代码如下

/**
 * @param {string[]} words
 * @return {number}
 */
var minimumLengthEncoding = function(words) {
    const tree = new trimTree();
    for(const word of words){
        tree.insert(word);
    }
    return tree.getNum();
};
class trimTree{
    constructor(){
        this.tree = {};
    };
    insert(word){
        let tree = this.tree;
        let wordLen = 0;
        for(let i = word.length - 1; i >= 0; i--){
            const w = word[i];
            !tree[w] ? tree[w] = {} : '';
            tree = tree[w];
            wordLen++;
        }
        tree.isStart = true;
        tree.wordLen = wordLen;
    };
    getNum(t = this.tree,num = 0){
        if(!t) return;
        for(let k in t){
            if(k === 'wordLen' && Object.keys(t).length == 2){
                num += t[k] + 1;
            }else if(k !== 'isStart') num += this.getNum(t[k]);
        }
        return num;
    }
}

公众号

关注公众号『前端也能这么有趣』，获取更多新鲜内容。

说在后面

这里是 JYeontu，现在是一名前端工程师，有空会刷刷算法题，平时喜欢打羽毛球 ，平时也喜欢写些东西，既为自己记录 ，也希望可以对大家有那么一丢丢的帮助，写的不好望多多谅解 ，写错的地方望指出，定会认真改进 ，偶尔也会在自己的公众号『前端也能这么有趣』发一些比较有趣的文章，有兴趣的也可以关注下。在此谢谢大家的支持，我们下文再见 。