数据结构之选择排序
目录
直接选择排序
选择排序的时间复杂度
堆排序
向上调整算法
向下调整算法
向上调整算法建立堆
向下调整算法建立堆
堆排序整体代码
堆排序的时间复杂度
直接选择排序
在之前讲插入排序时,我们讲了这样的一个应用场景,我们在斗地主摸牌时,会一张一张的摸,然后采用插入排序的方法将手中的牌变得有序,但是还有一种摸牌的方式,就是将所有的牌先发到手里,然后在所有牌中找出最大的和最小的放到牌的两端,重复上述步骤,依次挑选最大的和最小的放到两端,直到将手中的牌排好序,这其实就是生活中直接选择排序的应用。在数据结构中,直接选择排序又是怎样实现的呢?
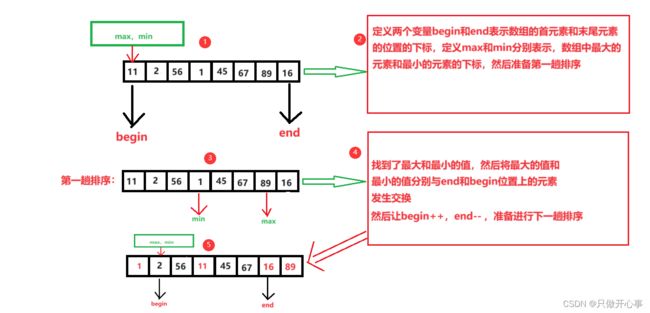
直接插入排序的思想:先进行单趟的排序,找出最小和最大的两个数,并且将最小的数和最大的数依次交换到数组的头部和尾部,然后重复单趟排序的操作,直到将数组整个排有序。
直接选择排序图示如下:
直接选择排序代码如下:
void Swap(int* p1, int* p2)
{
int temp = *p1;
*p1 = *p2;
*p2 = temp;
}
void SelectSort(int* a, int size)
{
int begin = 0, end = size - 1;
while (begin < end)
{
int max = begin, min = begin;
//先进行单趟排序,遍历每个元素,找出最大最小的两个数的位置
for (int i = begin+1; i <= end; i++)//这里让begin+1的原因是,自己没有必要和自己比较
{
if (a[i] < a[min])
{
min = i;
}
if (a[i] > a[max])
{
max = i;
}
}
//单趟排序找到最大和最小的元素之后,将最小的值与begin位置上的元素交换,将最大的值与end位置上的元素交换
Swap(&a[begin], &a[min]);
//当begin位置上的元素就是最大的元素时,将最小的元素和begin位置上的元素交换之后,最大的元素的位置就会发生改变
//max位置上的元素并不是最大的元素,min位置上的元素就是最大的元素,所以我们得把此时的min赋值给max,然后再做交换
if (max == begin)
max = min;
Swap(&a[end], &a[max]);
//让begin++,end--,再进行下一趟排序,找出最大的和最小的放置在两端
begin++;
end--;
}
}
int main()
{
int arr[] = {100,99,27,92,99,220,28,78,18,8 };
SelectSort(arr, sizeof(arr) / sizeof(int));
for (int i = 0; i < sizeof(arr) / sizeof(int); i++)
{
printf("%d ", arr[i]);
}
return 0;
}大家有没有注意到这样一段代码:
我们进行了一趟排序,找出了最大的元素和最小的元素,直接将最大的元素和最小的元素分别与end位置和begin位置上的元素交换即可,为什么还要把进行一次判断呢?
因为我们要排除一种极端的情况:
看下图:
其实对于上述情况,我们还有一种解决办法,如果begin位置的元素就是最大的元素,我们可以先让大的元素和end位置上的元素进行交换,然后再让最小的元素和begin位置上的元素进行交换,但是,上述情况只是在先交换最小元素的基础上修正的代码,大家可以根据自己情况进行选择。
选择排序的时间复杂度
时间复杂度:最好最坏都是O(N^2)
因为即使数组已经有序了编译器是无法分辨的,还是得每次找出最大的数和最小的数,第一趟比较每个元素比较2次所以总共比较2*(size-1)次,第二趟比较比较2*(size-3)次,所以其复杂度为等差数列的前n项求和,不管最好最坏,选择排序都是这个执行流程,所以直接选择排序的时间复杂度为O(N^2)。
稳定性:不稳定
堆排序
堆排序其实最重要的就是两个算法,向上调整和向下调整算法,先通过向上调整和向下调整算法建立堆,然后建好堆之后,再次采用向下调整算法调整元素的位置,最终实现排序。
以下给出具体的代码,对代码不理解的小伙伴可以去看堆那几期的内容。点击这里 and 这里
向上调整算法
void AdjustUp(int* a, int child)
{
assert(a);
int parent = (child - 1) / 2;
while (child > 0)
{
//因为是大堆,所以父亲节点的值大于孩子节点的值,如果父亲节点的值小于孩子节点的值,就需要交换
if (a[parent] < a[child])
{
int tmp = a[parent];
a[parent] = a[child];
a[child] = tmp;
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}向下调整算法
void AdjustDown(int* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child < n)
{
//因为是大堆,向下调整时,为了避免从堆顶继续调整,所以必须选最大的孩子作为child
if (child + 1 < n && a[child + 1] > a[child])
{
++child;
}
//因为是大堆,所以,如果父亲小于孩子,需要进行交换
if (a[parent] < a[child])
{
int tmp = a[parent];
a[parent] = a[child];
a[child] = tmp;
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}向上调整算法建立堆
for (int i = 1; i < n; i++)
{
AdjustUp(a, i);
}向上调整算法建堆,这里的i表示的就是向上调整算法里的child,对某个元素采用向上调整算法的前提是这个元素的前面的所有元素必须构成大堆或者小堆,对于一个数组而言,如果数组只有一个元素,我们就可以将这个数组看成大堆或者小堆,所以我们可以单独将第一个元素看成是一个大堆或者小堆,所以就可以从第二个元素要开始进行向上调整算法,然后后面的依此逻辑,直到将整个数组建成堆,与其说是建堆,不如说是调堆。
向下调整算法建立堆
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}向下调整算法建堆,这里的i可以看做向下调整算法里的parent,一个元素要采用向下调整算法,必须保证当前元素所在节点的左右子树都必须为大堆或者小堆。叶子节点没有左右子树,所以不能对叶子节点采用向下调整算法, 但是可以对最后一个叶子节点的父亲节点进行向下调整算法,因为最后一个叶子节点的父亲节点的左右子树都是叶子节点,叶子节点可以看成是一个大堆或者小堆,所以我们要从最后一个叶子节点的父亲节点开始进行向下调整算法。
堆排序整体代码
void HeapSort(int* a,int n)
{
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
for (int end = n - 1; end >= 0; end--)
{
HPDataType tmp = a[0];
a[0] = a[end];
a[end] = tmp;
AdjustDown(a, end, 0);
}
}
int main()
{
int arr[] = { 1000,999,27,9,99,20,28,78,18,88 };
HeapSort(arr, sizeof(arr) / sizeof(int));
for (int i = 0; i < sizeof(arr) / sizeof(int); i++)
{
printf("%d ", arr[i]);
}
return 0;
}运行截图:
堆排序的时间复杂度
时间复杂度:O(N*logN)
稳定性:不稳定
注意:虽然向上调整算法和向下调整算法都可以建立堆,但是我们建议使用向下调整算法建立堆,因为向上调整算法的时间复杂度为O(N*logN),而向下调整算法建立堆的时间复杂度为O(N)。
以上便是选择排序的所有内容。
本期的内容到此结束。^_^