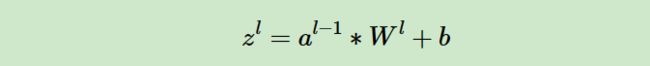【23-24 秋学期】NNDL 作业8 卷积 导数 反向传播

习题5-2  证明宽卷积具有交换性， 即公式(5.13)．

图像X和卷积核W的宽卷积定义如下：

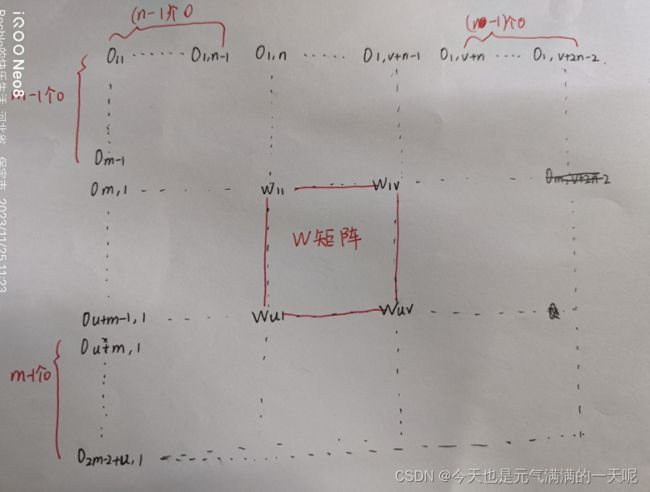
要证明：当图像X和卷积核W有固定长度时,他们的宽卷积具有满足交换性，如下：

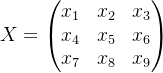
设二维图像为：，也就是：

对应卷积核为：，也就是：

可知，rot(X)为：

rot(W)为：

对X进行零填充，填充后的全填充图像为

对W进行零填充，填充后的全填充图像为

由于这俩图太难画，所以比照着3*3的X矩阵和2*2的W矩阵画在纸上：

如下图所示【W矩阵填充后】：

计算,如下图所示：

可以比较rot(X)和图像，可以看到，第一个相乘的元素是x11和w11，为了方便，我计算了四个角的值，可以推算出为：

：

如下：

【上图最上边红线范围错了，是】 

同理，得到：

故此证明交换性。

以上参考【【NNDL作业】 宽卷积具有交换性_卷积交换律公式证明_HBU_David的博客-CSDN博客】

习题5-4

(1)对于一个输入为100 × 100 × 256的特征映射组， 使用3 × 3的卷积核， 输出为100 × 100 × 256的特征映射组的卷积层， 求其时间和空间复杂度．

参考【一维卷积与一维平均池化的时间复杂度_池化层的时间复杂度-CSDN博客】

得到单个卷积层的时间复杂度：Time~O(M^2 * K^2 * Cin * Cout)

M:输出特征图（Feature Map）的尺寸。
K:卷积核（Kernel）的尺寸。
Cin:输入通道数。
Cout:输出通道数。

参考【NNDL 作业7：第五章课后题（1×1 卷积核 | CNN BP）_卷积核运算例题-CSDN博客】

得到单个卷积的空间复杂度：Space~O(K^2 * Cin * Cout+M^2*Cout)

---

 可知，M=100,K=3,Cin=256,Cout=256

---

可以求解：

时间复杂度=100*100*3*3*256*256=5898,240,000

空间复杂度=3*3*256*256+100*100*256=3,149,824

(2）如果引入一个1 × 1卷积核， 先得到100 × 100 × 64的特征映射， 再进行3 × 3的卷积， 得到100 × 100 × 256的特征映射组， 求其时间和空间复杂度．

---

可知，M1=100，K1=1，Cin1=256,Cout1=64;M2=100,K2=3,Cin2=64,Cout2=256

---

 可以求解：

时间复杂度=100*100*1*1*256*64+100*100*3*3*64*256=1638,400,000

空间复杂度=3*3*64*256+100*100*256=2,707,456

关于我自己的理解是空间复杂度至于最后一次卷积所占空间有关，后来参考【卷积神经网络的复杂度分析 - 超杰 (spytensor.com)】发现不对，他的解释如下：

其中提到层数，我理解这里的卷积层数指的是卷了几次，在本题中卷了两次，所以：

 空间复杂度=1×1×256×64+100×100×64+3×3×64×256+100×100×256=3363840

习题5-5 对于一个二维卷积， 输入为3 × 3， 卷积核大小为2 × 2， 试将卷积操作重写为仿射变换的形式． 参见公式(5.45) .

由题意得，二维卷积输入大小为：3*3，故将3×3输入展开成9维的。卷积核大小为2×2，共需要做四次卷积操作。

原来：

如下表所示：

输入3*3展开9维：

卷积核：

		0			0	0	0	0
0			0			0	0	0
0	0	0			0			0
0	0	0	0			0

附加题 阅读 “5.3.1 卷积神经网络的反向传播算法”，举例说明推导过程.

1.池化层反向传播

由于池化层没有激活函数，所以不需要求导计算，所以令() = ，则’ () = 1。

但是池化层对输入进行了压缩【以最大池化层Max Pooling为例】，我们需要做的是通过已知池化层的，推导出上一隐藏层的。

已知池化层：

那么上一层情况可以还原为：

假设在前向传播时记录的最大值位置分别是左上，右下，右上，左下，则转换后的矩阵为：

 其中使用upsample函数完成池化误差矩阵放大与误差重新分配的逻辑，得到公式如下：

2.卷积层反向传播

假设卷积层为，

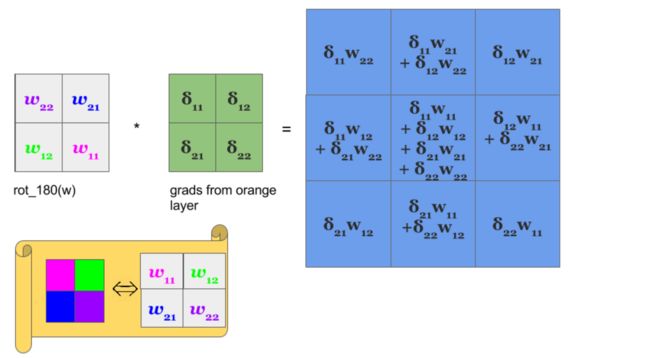
先看看卷积层的正向计算：【图来自Convolutional Neural Networks backpropagation: from intuition to derivation – Grzegorz Gwardys (wordpress.com)】

 根据习题5-7，可知卷积层的前向计算和反向传播是转置关系【证明看习题5-7】

也就是说上一层卷积层与本层的关系为：

 3.已知卷积层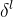，求解本层W和b

而池化层并没有W,b，也不用求W,b的梯度。只有卷积层的W,b需要求解：

卷积层z和W,b的关系为：

则对W求导：

 对b进行求导【将的各个子矩阵的项分别求和，得到一个误差向量，即为b的梯度】

进行反向传播计算时：

参考【卷积神经网络(CNN)反向传播算法 - 刘建平Pinard - 博客园 (cnblogs.com)】

习题 5-7 忽略激活函数， 分析卷积网络中卷积层的前向计算和反向传播（公式(5.39)） 是一种转置关系．

以习题5-5为例，其中：

卷积：以后，得到Y:

在5-3中也知道了W和X的展开情况，从展开情况可以看出，y的4个值是展开4*9的卷积核【一行9个】通过展开9维的X【一列9个】相乘得到的，那么可以推出：

上式即为前向计算。

反向计算，也就是求loss关于x的导得到一个x关于y的关系式；

由于反向求解是使用4个y得到每个x，所以：

已知y和x的关系，所以：

所以：

可以看到，和，前向计算和反向传播是转置关系。

也就是：

以上参考了【【23-24 秋学期】NNDL 作业8 卷积 导数 反向传播-CSDN博客】 

【神经网络与深度学习[邱锡鹏] 第五章习题解析 - whyaza - 博客园 (cnblogs.com)】

习题5-8 在空洞卷积中， 当卷积核大小为， 膨胀率为时， 如何设置零填充的值以使得卷积为等宽卷积 .

1.空洞卷积的概念

空洞卷积引入了一个称为 “扩张率(dilation rate)”的超参数(hyper-parameter)，该参数定义了卷积核处理数据时各值的间距。扩张率中文也叫空洞数(Hole Size)。

 其中

• a是普通的卷积过程(dilation rate = 1),卷积后的感受野为3

• b是dilation rate = 2的空洞卷积,卷积后的感受野为5

• c是dilation rate = 3的空洞卷积,卷积后的感受野为8

 计算方式为：’ = + ( − 1) × ( − 1)【D是膨胀率，D-1是每两个插入的空洞数，K是原来的感受野/卷积核大小】

以上参考【深入理解空洞卷积 (qq.com)】

 2.等宽卷积的概念

 假设卷积层的输入神经元个数为 ，卷积大小为 ，步长为 ，在输入两端各填补 个 0
（zero padding），那么该卷积层的神输出经元数量为 ：( − + 2)/ + 1

卷积的结果按输出长度不同可以分为三类（表示卷积核长度）：
1）窄卷积 ：步长 =1，两端不补零 =0 ，卷积后输出长度为 − + 1；
2）宽卷积 ：步长 =1，两端补零 = − 1 ，卷积后输出长度 + − 1；
3）等宽卷积 ：步长 =1，两端补零 =( − 1)/2 ，卷积后输出长度 ；
参考【深度学习之 10 卷积神经网络1_如何求等宽卷积-CSDN博客】

3.求解

已知现在的卷积核大小为K，膨胀率是D，可求出新的卷积核大小为K1=K+(K-1)*(D-1)

再根据上边等宽卷积的概念，可知：P=(K1-1)/2,也就是P=[K+(K-1)*(D-1)-1]/2

化简后为：P=D*(K-1)/2

总结

目前感觉卷积最难的地方在求解反向传播，还有证明上，感觉各种数学式子看起来比较费劲，在这里我试试不带数学式的总结一下：

1，证明宽卷积具有交换性

这个我看到的有直接以3*3输入、2*2卷积为例证明的，但是这样的证明不具有普遍性，后来我还是参考了老师的博客写的：

【【NNDL作业】 宽卷积具有交换性_卷积交换律公式证明_HBU_David的博客-CSDN博客】

 其中想要证明交换性：首先举出一个无穷大的矩阵X：m*n,卷积W：u*v,然后分别求解他们的rot180，再进行零填充【以对X0填充为例】，要求是两边m-1,两边n-1，然后与W相乘，得到一个数；另一边反过来，得到一个数，如果相等则得证。

2，求解时间空间复杂度

记住公式直接套，其中我有疑问并修改了的是第二小问：有两个卷积核，求空间复杂度。

在【卷积神经网络的复杂度分析 - 超杰 (spytensor.com)】写的比较明白，空间复杂度要算这两次卷积的总和。

3，卷积神经网络的反向传播

这个是真的很让我难受啊，扣了半天手指，大概思路如下：

你要想求解反向传播，你必须了解正向是怎么走的：

 图来自【卷积神经网络与迁移学习 卷积神经网络推导_mob6454cc692b0f的技术博客_51CTO博客】

其中有两个关键层【卷积层和池化层】，这时候我还想到了批量规范化层，但是没搜到相关资料，就没求这部分。

对于池化层，使用一个函数就可以推导出池化前的矩阵【upsample】

对于卷积层，求解上一层可以根据上一层与本层关系【转置】来求解

求解卷积层的W和b，和前边学过的前馈神经反向传播有点类似，使用损失求解，b有点不同，b的梯度是各个子矩阵的项分别求和，得到一个误差向量。

4.分析卷积网络中卷积层的前向计算和反向传播（公式(5.39)） 是一种转置关系

证明转置关系关键的一环是：求解X关于loss的导，可以得到X与Y的一个反向关系。这样就能证明了。

5，设置零填充的值以使得卷积为等宽卷积

考察概念：什么是等宽、什么是空洞卷积、什么是膨胀率，然后记住公式就可求解。