Nova中 Vitalik R1CS例子 的 folding scheme

1. 引言

前序博客有：

• Nova代码解析
• Spartan中 Vitalik R1CS例子 SNARK证明基本思路
• rank-1 constraint system R1CS

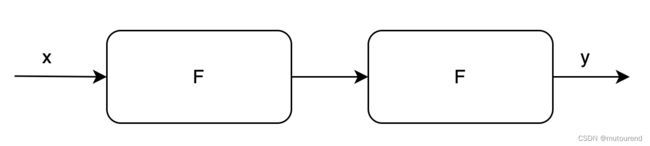
其中$F(x)=x^3+x+5$，注意其中$x,y$均为public input/output。以连续调用两次为例，代码见：

• https://github.com/Microsoft/Nova（Rust）

对IVC proof进行SNARK压缩，有两种压缩实现：

• 1）spartan::RelaxedR1CSSNAR：使用Spartan + IPA-PC作为多项式承诺方案。
• 2）spartan::pp::RelaxedR1CSSNARK：使用Spartan + sum-check，并将向量承诺看成是对多项式的承诺。

  type S1<G1> = spartan::RelaxedR1CSSNARK<G1, EE1<G1>>;
  type S2<G2> = spartan::RelaxedR1CSSNARK<G2, EE2<G2>>;
  type S1Prime<G1> = spartan::pp::RelaxedR1CSSNARK<G1, EE1<G1>>;
  type S2Prime<G2> = spartan::pp::RelaxedR1CSSNARK<G2, EE2<G2>>;

src/nifs.rs中的测试用例：

• 1）test_tiny_r1cs_bellperson() ：基于https://github.com/filecoin-project/bellperson框架。
• 2）test_tiny_r1cs() ：直观表示。

  #[test] 
  fn test_tiny_r1cs_bellperson() { // 基于[https://github.com/filecoin-project/bellperson](https://github.com/filecoin-project/bellperson)框架
    test_tiny_r1cs_bellperson_with::<G>();
  }
  
  #[test]
  fn test_tiny_r1cs() { //直观表示
    test_tiny_r1cs_with::<pasta_curves::pallas::Point>();
  }

src/lib.rs中：

• test_ivc_nontrivial测试用例中：
  • $F_1(x)=x$，当初始输入为1，迭代3次时，输出为1；
  • $F_2(x)=x^3+x+5$，当初始输入为0，迭代3次时，输出为2460515。

  #[test]
  fn test_ivc_nontrivial() {
    type G1 = pasta_curves::pallas::Point;
    type G2 = pasta_curves::vesta::Point;

    test_ivc_nontrivial_with::<G1, G2>();
  }
fn test_ivc_nontrivial_with<G1, G2>()
  where
    G1: Group<Base = <G2 as Group>::Scalar>,
    G2: Group<Base = <G1 as Group>::Scalar>,
  {
    let circuit_primary = TrivialTestCircuit::default();
    let circuit_secondary = CubicCircuit::default();

    // produce public parameters
    let pp = PublicParams::<
      G1,
      G2,
      TrivialTestCircuit<<G1 as Group>::Scalar>,
      CubicCircuit<<G2 as Group>::Scalar>,
    >::setup(circuit_primary.clone(), circuit_secondary.clone());

    let num_steps = 3;

    // produce a recursive SNARK
    let mut recursive_snark = RecursiveSNARK::<
      G1,
      G2,
      TrivialTestCircuit<<G1 as Group>::Scalar>,
      CubicCircuit<<G2 as Group>::Scalar>,
    >::new(
      &pp,
      &circuit_primary,
      &circuit_secondary,
      vec![<G1 as Group>::Scalar::ONE],
      vec![<G2 as Group>::Scalar::ZERO],
    );

    for i in 0..num_steps {
      let res = recursive_snark.prove_step(
        &pp,
        &circuit_primary,
        &circuit_secondary,
        vec![<G1 as Group>::Scalar::ONE],
        vec![<G2 as Group>::Scalar::ZERO],
      );
      assert!(res.is_ok());

      // verify the recursive snark at each step of recursion
      let res = recursive_snark.verify(
        &pp,
        i + 1,
        &[<G1 as Group>::Scalar::ONE],
        &[<G2 as Group>::Scalar::ZERO],
      );
      assert!(res.is_ok());
    }

    // verify the recursive SNARK
    let res = recursive_snark.verify(
      &pp,
      num_steps,
      &[<G1 as Group>::Scalar::ONE],
      &[<G2 as Group>::Scalar::ZERO],
    );
    assert!(res.is_ok());

    let (zn_primary, zn_secondary) = res.unwrap();

    // sanity: check the claimed output with a direct computation of the same
    assert_eq!(zn_primary, vec![<G1 as Group>::Scalar::ONE]);
    let mut zn_secondary_direct = vec![<G2 as Group>::Scalar::ZERO];
    for _i in 0..num_steps {
      zn_secondary_direct = circuit_secondary.clone().output(&zn_secondary_direct);
    }
    assert_eq!(zn_secondary, zn_secondary_direct);
    assert_eq!(zn_secondary, vec![<G2 as Group>::Scalar::from(2460515u64)]);
  }

• test_ivc_nontrivial_with_compression则在test_ivc_nontrivial测试用例的基础之上，使用CompressedSNARK对结果进行了进一步压缩：

	// produce a compressed SNARK
    let res = CompressedSNARK::<_, _, _, _, S1<G1>, S2<G2>>::prove(&pp, &pk, &recursive_snark);
    assert!(res.is_ok());
    let compressed_snark = res.unwrap();

    // verify the compressed SNARK
    let res = compressed_snark.verify(
      &vk,
      num_steps,
      vec![<G1 as Group>::Scalar::ONE],
      vec![<G2 as Group>::Scalar::ZERO],
    );
    assert!(res.is_ok());

• test_ivc_nontrivial_with_spark_compression则在test_ivc_nontrivial测试用例的基础之上，使用Spark compiler对结果进行了进一步压缩：

	// run the compressed snark with Spark compiler

    // produce the prover and verifier keys for compressed snark
    let (pk, vk) = CompressedSNARK::<_, _, _, _, S1Prime<G1>, S2Prime<G2>>::setup(&pp).unwrap();

    // produce a compressed SNARK
    let res =
      CompressedSNARK::<_, _, _, _, S1Prime<G1>, S2Prime<G2>>::prove(&pp, &pk, &recursive_snark);
    assert!(res.is_ok());
    let compressed_snark = res.unwrap();

    // verify the compressed SNARK
    let res = compressed_snark.verify(
      &vk,
      num_steps,
      vec![<G1 as Group>::Scalar::ONE],
      vec![<G2 as Group>::Scalar::ZERO],
    );
    assert!(res.is_ok());

• test_ivc_nondet_with_compression中：
  • $F_1(x)=x^{1/5}$，迭代调用3次。
  • $F_2(x)=x$，迭代调用3次。

Nova系列博客

• Nova: Recursive Zero-Knowledge Arguments from Folding Schemes学习笔记
• Nova 和 SuperNova：无需通用电路的通用机器执行证明系统
• Sangria：类似Nova folding scheme的relaxed PLONK for PLONK
• 基于Nova/SuperNova的zkVM
• SuperNova：为多指令虚拟机执行提供递归证明
• Lurk——Recursive zk-SNARKs编程语言
• Research Day 2023：Succinct ZKP最新进展
• 2023年 ZK Hack以及ZK Summit 亮点记
• 基于cycle of curves的Nova证明系统（1）
• 基于cycle of curves的Nova证明系统（2）
• Nova代码解析