ODE手册（2）基本概念

说明：本手册翻译自ODE官方Manual

---

 

　　2.1 背景介绍

　　我会在这里陆续写一些关于刚体动力学和机器仿真的背景知识。但是在此期间，请参看Baraff's的SIGGRAPH（Special Interest Group on Computer Graphics：美国计算机协会绘图专业组）指南。

　　刚体：从计算机仿真的角度来看，一个刚体包含若干个属性，其中一些属性会随着时间的改变而发生改变:

• 刚体的位置：用向量（x,y,z）表示刚体的位置（基准点），通常情况下基准点的选取必须跟刚体的质点一致
• 刚体的方位：用一个四元组（qs,qx,qy,qz）或者一个2x2的旋转矩阵表示
• 刚体的线速度：用向量（vx,vy,vz）表示（基准点的线速度）
• 刚体的角速度：用向量（wx,wy,wz）表示，用以描述刚体的方位随时间的变化

　　而另外一些属性则是恒定不变的，它们不随时间的改变而改变：

• 刚体的质量
• 刚体质点相对于基准点的位置，在一般的实现中刚体的质点和基准点是一致的
• 惯性矩阵：用一个2x2的矩阵描述刚体的质量在质点周围的分布。从概念上讲，每一个刚体都会有一个x-y-z坐标系嵌在刚体上，和刚体一同移动、旋转，如下图1所示：

　　　　　　　　　　　　

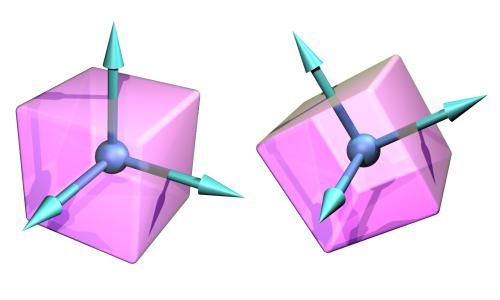
　　图1：刚体的坐标系

　　坐标系的原点即为刚体的基准点，在ODE中有一些值（向量、矩阵等）是相对于刚体的坐标系的，而其它的值是相对于全局坐标系的。 另外需要注意的是：刚体的形状不是一个动态的属性（除了在它会影响到许多质量属性时），只有在碰撞检测中会考虑到它的形状细节。

　　2.2 刚体“岛屿”（群）和刚体的禁用

　　刚体之间通过关节相互连接，一个刚体“岛屿”（群）由一组不能被拉开的刚体组成——换句话说就是，“岛屿”（群）中的每个刚体都和“岛屿”（群）中的其它刚体之间以某种方式相互连接。

　　只要仿真一开始进行，存在于仿真环境中每个“岛屿”（群）都会被单独处理。这样做有利于理解：如果有N个“岛屿”（群）在被仿真，那么本次仿真计算的时间复杂度就为O(N)。

　　每一个刚体都可以被启用或禁用。在一次仿真中被禁用的刚体将被有效地“关闭”并且不再更新。禁用刚体是一种节省计算时间的有效方法，被禁用后的刚体在仿真过程中是静止的，并且与仿真过程无关。

　　一个“岛屿”（群）中只要有任何一个刚体处于启用状态，那么在下一步的仿真中“岛屿”（群）中的所有刚体都会被启用。因此要有效地禁用一个“岛屿”（群）中的刚体，那么在“岛屿”（群）中的任何一个刚体都要被禁用。如果一个被禁用的“岛屿”群被其它任意一个启用的刚体接触到，那么这个“岛屿”（群）中的所有刚体都会被启用，就像一个连接关节一样把启用的刚体添加到自己的“岛屿”（群）中。

　　2.2 积分

　　我们把刚体系统在一段时间内的仿真过程称做一次积分。每一次积分都会花费一个指定的时间步长，并且把所有刚体的状态调整到新时刻的状态。无论使用哪一种积分器，都不可避免的需要考虑一下两个问题：

• 它有多精确？就是说仿真系统的仿真结果与相应于现实世界中的状态有多接近？
• 它有多稳定？是不是任何的计算错误都会导致仿真系统产生完全非物理的结果（例如，致使系统毫无缘由地出现“爆炸”）？

　　ODE当前使用的积分器是相当稳定的，但是不是足够精确（除了选择的步长很小）。对于大多数ODE应用来说，这不算一个问题——在几乎所有的案例中，ODE的行为仍然十分完美的遵循物理规律。当然，ODE不应该被使用在十分精确的数量工程中，除非它的精确度在未来的版本中被改进。

　　2.4 蓄力器

　　在每一个积分步（一个时间步长下的积分过程）中，用户可以调用函数给刚体施加力，这些力用过“蓄力器”施加到刚体上。当下一次积分步开始的时候，所有施加的力就会作用在刚体上。每一个积分步之后，蓄力器就会被清零。

　　2.5 关节和约束

　　显示生活中的关节是一个像铰链一样的东西，常用来连接两个物体。ODE中的关节也是相似的：它是一种强制施加在两个刚体之间的关系，以使它们相互之间具有一定的位置和方位（朝向）。这种关系就称作约束——关节和约束常常交换使用。下面图2展示了2种不用的约束类型：

　　

　　　　　　　　　　图2：2中不同的约束（关节）类型（从左至右分别为:球窝、铰链、滑动

　　第一个是球窝关节，用以约束一个刚体的“球”始终在另一个刚体的“窝”的同一位置处。

　　第二个是铰链关节，用以约束铰链的两部分始终在同一位置并且以铰链轴联接在一起。

　　第三个是滑动关节，用以约束“活塞”和“气缸”联接起来，另外还约束两个刚体拥有相同的方位（朝向）。

 　　在积分器所花费的每一个时间步长之内，所有的关节都被允许施加约束到它们所影响的刚体上。这些力的计算使得刚体的以某种方式移动，但又不会破坏所有刚体之间的约束关系。

 　　每个关节都有若干个参数去控制它的几何形状，一个很好的例子就是：球窝关节上一个点的位置。设置关节参数的函数一律采用全局坐标，而不是相对于刚体的坐标。另外需要注意到一点事，一个关节所连接的刚体在被关节连接起来之前必须被正确放置。

　　2.6 关节组

　　关节组是一个特殊的容器，用于将某些关节封装在一起。关节可以被添加到一个指定的组中，一旦当这些关节不再需要时，就可以通过一个函数调用快速地销毁掉整个关节组。当然，在组中的单个关节也可以在组被清空前销毁掉。这种方法对连接关节是非常有用的，通过在一个时间步长内向组中添加关节或者从组内移除关节。

　　2.7 关节误差和误差降低参数（暂定）（Error reduction Parameter-ERP）

　　当用一个关节连接两个刚体时，两个刚体之间必须得有相互确定的位置和方位。当然，刚体的位置超出关节的约束范围也是可能发生的。这种关节故障会以下面两种方式发生：

• 用户只正确地设置了一个刚体的位置和方位，而没有设置另一个刚体的位置和方位
• 在仿真期间，错误会致使刚体从它们本应该所处的位置慢慢地移走

　　下面图2展示了一个球窝关节 误差的例子（“球”跟“窝”没有联接起来）：

　

图2：球窝关节误差

　　有这样一种方法可以降低关节误差：在每一个积分步之内，给每个关节施加一个特殊的力(校正力)让它们回到自己的正确位置。这个力就是被误差降低参数（ERP）控制的，它的取值范围为[0,1]。

　　ERP参数限定了在下一次仿真步进之内什么样的误差将会被修正。如果ERP=0就意味着不会有任何校正力施加在刚体上，随着仿真的进行刚体最终会偏离应处的位置。如果ERP=1则意味着仿真器将会在下一个时间步长中努力消除所有的关节误差。当然，我们并不推荐将ERP的值设为1，因为仿真器内部存在的各种各样的近似计算，关节误差是不会被完全修正的。建议将ERP的范围限制在[0.1,0.8]（默认选用ERP=0.2）.

　　通过设定全局范围的ERP参数将会影响仿真过程中的大多数关节，然而一些关节也会有自己的ERP参数值去控制它的方方面面。

　　2.8 软约束和混力约束因子(暂定)（Constraint Force Mixing-CFM）

　　大多数的约束都属于”硬约束“，这就意味着约束条件永远不会被打破。例如，球窝关节的”球“必须总是在”窝“中，铰链关节的两部分必须总是联接在一起。在实际的仿真过程中，约束会被不知不觉中引入到系统中的误差打破，但是会有误差降低参数来修正这些误差。

　　也并不是说所有的约束都是”硬约束“，一些”软约束“就是被设计用来打破的。例如，用来阻止碰撞物体之间相互侵入的接触约束在默认情况下是”硬约束“，用来模拟好像物体的碰撞面是由钢铁做的，但是它也可以被设定为”软约束“用来模拟较为松软的材料。真是因为这样”软约束“的存在，我们才能得以模拟当两个物体被强行放在一起时的自然挤压。

　　模拟器会通过两个参数来控制”软“、”硬“约束之间的区别。第一个就是前面所介绍的ERP，另一个就是CFM（将在下面介绍）

　　　　2.8.1 混力约束因子（CFM）:

　　　　下面是一些关于CFM含义的专业描述，如果你只是想知道怎样在实际模拟中使用它，就跳过这一节到下一部分。

　　　　一般的关节约束方程的形式为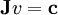：　　　　其中：

　　　　　　V: 表示刚体的速度向量

　　　　　　J：是一个雅克比矩阵，它的一列用来表示从系统中移除的关节的每一个自由度

　　　　　　c：是一个右手向量

　　　　在下一个时间步长之内，通过计算向量λ（大小和c一样）以使施加在刚体上的力保护关节的约束：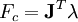

　　　　ODE新添加了一个变换，它的约束方程的形式为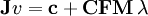：　　　　其中：

　　　　　　CFM：是一个对角矩阵，CFM将所有约束力产生的结果和约束联系在一起。一个非0（正数）的CFM值允许原约束方程被一定比例的CFM乘以用于增强约束的恢复力λ所打破。给定λ求解如下：　　

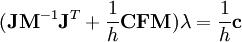
　　这里CFM只是简单地叠加到原系统矩阵的对角上。在CFM为正时，它可以使得系统原理任何奇点，从而改善可分解因子的精确度。

　　　　2.8.2 怎样去使用ERP和CFM？

　　　　 在许多关节中ERP和CFM都会被单独设定。你可以在接触关节、连接限制和很多其他场合下使用它们去控制关节（或连接限制）的柔性和弹性。

　　　　如果一个关节的CFM值被设为0，它就是一个硬关节；如果被设为正值，它就有可能在推力的作用下冲破约束（例如，对于强制将两个物体连接在一起的接触约束），换句话说，这种约束属于“软”约束而且它的柔软性将会随着CFM的增大而增强。如果一定比例的CFM乘以用于增强约束的恢复力时，这种约束就回被打破。注意，如果将CFM设为一个负值将会给我们带来出乎预料的糟糕影响，诸如不稳定性。

　　　　通过调整ERP和CFM的值，你可以实现多种多样的模拟效果。例如，你可以模拟两个物体像被弹簧联接在一起振荡的弹性约束，或者模拟更多的没有振荡的柔性约束。事实上，通过选定不同的ERP和CFM值，你会得到任何你想实现的弹性约束和阻尼约束效果。如果你设定了一个弹性约束k_p和一个阻尼约束k_d，与此相一致的ODE约束方程为：

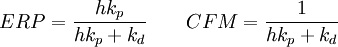　　其中，h是步进长度。这些值将会给同样适用隐含一阶积分的弹性-阻尼系统带来相同的效果。适当地增加CFM的值，尤其是全局CFM的值，可以有效地降低模拟的数值型误差。如果系统是接近奇性的，这样可以显著地增强稳定性。事实上，如果系统失控了，第一件应该尝试的解决方法就是去增加全局CFM的值。

　　2.9 碰撞处理

　　关于碰撞处理，这里有很多需要介绍的东西。

　　我们队发生在物体之间的碰撞或者物体与所处的静态环境之间的碰撞做如下处理：

• 在每一次仿真步之前，用户通过调用碰撞检测函数来确定到底是谁和谁在接触。这些函数会返回一个接触点的列表，每一个接触点确定空间中的一个点、一个面法向量和一个穿透深度。
• 在每一个接触点上创建一个特殊的接触关节，它由跟接触相关的其它信息所确定。例如，接触面之间的摩擦力，弹性和柔性强度以及许多其它的属性。
• 将接触关节添加到关节组（允许关节被快速地添加到系统或从系统中删除）中。接触关节越多，模拟的时间就越长，为此有很多种策略用于限制接触关节的数量。
• 开始进行仿真模拟。
• 移除系统中所有的接触关节

　　需要说明的一点：不一定非得使用系统内建的碰撞检测函数，只要提供的各种接触点信息是匹配的，你就可以使用其它的碰撞检测函数库。

　　2.10 典型的模拟代码

　　在这里介绍一种很典型的模拟过程：

• 创建一个动力学“世界”（可以理解为一种特殊的“环境”）
• 在此“世界”中创建各种刚体
• 设定各个刚体的状态（位置等）
• 在动力学“世界”中创建关节
• 联结关节到刚体上
• 设定所有关节的参数
• 如果需要，创建一个碰撞“世界”和一个碰撞几何体对象
• 创建一个关节组纳入所有的接触关节
• 循环
  • 给刚体施加力，依具体情况而定
  • 调整关节参数，依具体情况而定
  • 调用碰撞检测函数
  • 为每一个碰撞点创建接触关节，并且将其添加到接触关节组中
  • 开始仿真步
  • 从接触关节组中移除所有关节
• 销毁动力学以及碰撞“世界”

　　注：个人对所谓“世界”的理解：

　　我们所生活居住的现实世界是一个遵循各种物理规律、自然法则、道德约束的世界，在我们的认知范围内，我们是这个世界的统治者。在计算机所模拟的世界中，各种模拟对象之间也遵循一定的规则约束，为了便于计算机的模拟，我们将其中的各种规则划分开来，仅仅是因为易于用户理解、利于计算机模拟。谁又能说我们所生活的世界不是这样一个由“计算机”模拟的世界呢 ;-)

　　2.11 物理模型

　　这一部分，我们将简要介绍一下在ODE中使用的各种方法和近似。

　　　　2.11.1 摩擦近似

　　　　我们真的需要很多的图片来说明问题 ;)

　　　　

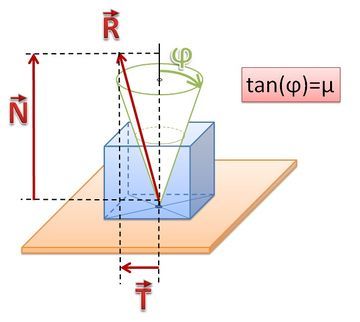　　　　　　　　　　　　　　　　　　　　　　　　图：摩擦角

 　　　　Coulomb摩擦力模型对接触点的摩擦力进行模型化来说是一种简单而有效的方法，我们用它来描述在接触点法线和切线方向上的力（参见接触关节部分对这些力的描述）之间的关系。遵循如下规则：

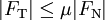　　　　其中：

　　　　F_T和F_N分别表示法线和切线方向的力

　　　　μ是摩擦系数（通常在1.0左右）

　　这个方程定义了一个“摩擦锥体”—试想一个以F_N为轴线，接触点为向量的锥体。如果所有的摩擦力向量都在锥体的内部，接触点就处于“粘结模式”，也就是说摩擦力足够大到防止接触面在彼此之间来回移动；如果在锥体表面，接触点就处于“滑动模式”，也就是说摩擦力不足够大到能够防止接触的滑动。参数μ确定了切线方向和发现方向力的最大比率。

　　为了只求效能，在ODE中使用的摩擦力模型近似于“摩擦锥体”。当前我们提供两种近似方法以供选择：

• μ本身的物理意义被改变，用以描述在一个接触面上最大的摩擦力（切线方向），或者切线摩擦力的方向。这种方法虽然是“非物理”的（因为它独立于法线方向的摩擦力），但是却是很有效而且是最廉价的计算量。注意在这种情况下，μ被用来描述对一个力的限制，而且是在模拟中必须适当选择的参数。
• 摩擦锥体在这里的近似，是通过一个和第一、第二摩擦方向相一致的摩擦力金字塔来实现的。然而更进一步的近似是这样的：首先ODE计算法线力（假设所有的接触都是无摩擦的），然后根据F_m = μ | F_N | 计算F_m对摩擦力（切线）的最大限制，最后继续求解整个系统在这些确定限制（μ）作用下的结果（以一种和上面提到的第一种近似法相似的方法）。这样不同于一个真正的摩擦力金字塔—μ的值是不确定的。这种近似方法更容易把μ当作一个无量纲量使用就像正常的Coloumb摩擦系数，因此它可以被设定为一个在1.0左右的常数而不用去在意具体的仿真实例。

　　这一部分的内容终于翻译完了，但是瑕疵很多，仍在不断修正中。。。望见谅;-)