个人项目Individual Project:n皇后问题
源码的github链接:
https://github.com/luhan420/test/tree/master
1.需求分析
在本次的课程设计中,用到的知识点主要有:类、函数、选择结构里的条件语句、循环结构里的while语句以及for循环语句、控制语句里的break语句、以及字符串函数的运用等等,并且应用到递归、回溯及穷举等比较经典的算法。
2.概要设计
类定义
类就是用户自定义的数据类型。
类定义的一般形式如下:
class 类名
{
细节;(数据成员,成员函数)
};
类函数定义
类成员函数类的成员函数通常在类外定义,一般形式如下:
返回类型 类名::函数名(形参表)
{
函数体;
}
双冒号: :是域运算符,主要用于类的成员函数的定义。
函数
函数的定义
定义函数需要指明:函数执行结果返回值的类型、函数名、形式参数(简称形参)和函数体。
一般形式为:
数据类型 函数名(行参表)
{
语句序列;
Return 合适类型数值
}
数据类型
规定了函数返回值类型。党执行函数体中的语句后,通常会产生一个结果,这就是函数的返回值,它可以是任何有效的类型。若函数执行后不返回值,数据类型习惯用void来表示。如果在函数定义时没有数据类型出现,则默认为函数返回值为整型值(int)。
函数调用
调用一个函数之前必须对该函数进行说明。
函数调用由函数名和函数调用运算符( )组成,( )内有0个或多个逗号分隔的参数(称为实参)。每一个参数是一个表达式,且参数的个数与参数的类型要与被调函数定义的参数(称为形参)个数和类型匹配。
当被调函数执行时,首先计算实参表达式,并将结果值传送给行参,然后执行函数体,返回的返回值被传送到调用函数。
如果函数调用后有返回值,调用表达是可以用在表达式中,而无参函数的调用是一个单独的语句。
用if语句实现选择结构设计
if语句的基本形式可分为两种:
(1) if (表达式) 语句
其执行过程是,首先计算表达式的值,若不为0,条件判断为真,则执行( )后面的语句,否则,if语句中止执行,即不执行( )后面的语句。
(2) if(表达式) 语句1
else 语句2
其执行过程是,首先计算表达式的值,若不为0,条件判断为真,则执行( )后面的语句,否则执行语句2。
if语句嵌套
if语句中的任何一个子句可以是任意可执行语句,当然也可以是一条if语句,这种情况称为if语句嵌套。当出现if语句的嵌套时,不管书写格式如何,else格式都将与它前面最靠近的未曾配对的if语句相配对,构成一条完整的if语句。它的格式为:
if(表达式1) 语句1;
else if (表达式2) 语句2;
……
else if (表达式n) 语句n;
else 语句n+1;
while和do-while语句
while语句用来实现“当型”循环结构,即先判断表达式,然后判断循环条件是否成立。其一般形式为:
do
{
语句;//循环体
}while(条件表达式);
其中要注意的是while后面的括号理是表达式而不是语句,表达式是没有分号的;而do-while中最后结束时要有分号。
循环结构
for语句
这种循环语句不仅用于循环次数已知的情况,还能用于循环次数预先不能确定只给出循环结束条件的情况下。
for 语句的一般形式:
for (表达式1;表达式2;表达式3)
{
语句;//循环体
}
其执行的过程有以下几个步骤:
求解表达式1;
求解表达式2,若其值为真,则执行for语句中指定的循环体语句,然后执行下面的第3)步。若为假,则结束循环;
求解表达式3;
转回上面第2)步继续执行;
循环结束,执行for语句后面的其他语句。
Break语句
该语句被限定使用在任一种循环语句和switch语句中,但break语句仅仅退出包含该break语句的那层循环,即break语句不能使程序控制退出一层以上的循环。
字符串处理函数
字符比较函数strcmp
格式:strcmp(字符串1,字符串2)
它的功能是,比较字符串1和字符串2。
如果字符串1小于字符串2,该函数返回一个负整数值;如果字符串1等于字符串2,该函数返回0;如果字符串1大于字符串2,该函数返回一个正整数值。
总体方案
显然问题的键在于如何判定某个皇后所在的行、列、斜线上是否有别的皇后;可以从矩阵的特点上找到规律,如果在同一行,则行号相同;如果在同一列上,则列号相同;如果同在\斜线上的行列值之和相同;如果同在/斜线上的行列值之差相同;如果斜线不分方向,则同一斜线上两皇后的行号之差的绝对值与列号之差的绝对值相同。下图是一个范例(图2-1是八皇后排列方式在vs6.0中的结果显示,图2-2是棋盘中八皇后位置显示)
将把皇后问题用三种方法表示出来,三种方法用switch语句连接.
○ ● ○ ○ ○ ○
图 2-1 “1”作为皇后
● ○ ○ ○ ○ ○ ○ ○
○ ○ ○ ○ ● ○ ○ ○
○ ○ ○ ○ ○ ○ ○ ●
○ ○ ○ ○ ○ ● ○ ○
○ ○ ● ○ ○ ○ ○ ○
○ ○ ○ ○ ○ ○ ● ○
○ ○ ○ ○ ○ ○ ○ ●
○ ○
图2-2 棋盘中的八皇后位置显示
3.详细设计
递归法
递归是指函数/过程/子程序在运行过程序中直接或间接调用自身而产生的重入现像.
递归算法一般用于解决三类问题:
(1)数据的定义是按递归定义的。(Fibonacci函数)
(2)问题解法按递归算法实现。(回溯)
(3)数据的结构形式是按递归定义的。(树的遍历,图的搜索)
能采用递归描述的算法通常有这样的特征:为求解规模为N的问题,设法将它分解成规模较小的问题,然后从这些小问题的解方便地构造出大问题的解,并且这些规模较小的问题也能采用同样的分解和综合方法,分解成规模更小的问题,并从这些更小问题的解构造出规模较大问题的解。
回溯法
回溯算法也叫试探法,它是一种系统地搜索问题的解的方法。按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
可用回溯法求解的问题P,通常要能表达为:对于已知的由n元组(x1,x2,…,xn)组成的一个状态空间E={(x1,x2,…,xn)|xi∈Si ,i=1,2,…,n},给定关于n元组中的一个分量的一个约束集D,要求E中满足D的全部约束条件的所有n元组。其中Si是分量xi的定义域,且 |Si| 有限,i=1,2,…,n。我们称E中满足D的全部约束条件的任一n元组为问题P的一个解。
回溯法首先将问题P的n元组的状态空间E表示成一棵高为n的带权有序树T,把在E中求问题P的所有解转化为在T中搜索问题P的所有解。树T类似于检索树,它可以这样构造:
设Si中的元素可排成xi(1) ,xi(2) ,…,xi(mi-1) ,|Si| =mi,i=1,2,…,n。从根开始,让T的第I层的每一个结点都有mi个儿子。这mi个儿子到它们的双亲的边,按从左到右的次序,分别带权xi+1(1) ,xi+1(2) ,…,xi+1(mi) ,i=0,1,2,…,n-1。照这种构造方式,E中的一个n元组(x1,x2,…,xn)对应于T中的一个叶子结点,T的根到这个叶子结点的路径上依次的n条边的权分别为x1,x2,…,xn,反之亦然。另外,对于任意的0≤i≤n-1,E中n元组(x1,x2,…,xn)的一个前缀I元组(x1,x2,…,xi)对应于T中的一个非叶子结点,T的根到这个非叶子结点的路径上依次的I条边的权分别为x1,x2,…,xi,反之亦然。特别,E中的任意一个n元组的空前缀( ),对应于T的根。
因而,在E中寻找问题P的一个解等价于在T中搜索一个叶子结点,要求从T的根到该叶子结点的路径上依次的n条边相应带的n个权x1,x2,…,xn满足约束集D的全部约束。在T中搜索所要求的叶子结点,很自然的一种方式是从根出发,按深度优先的策略逐步深入,即依次搜索满足约束条件的前缀1元组(x1i)、前缀2元组(x1,x2)、…,前缀I元组(x1,x2,…,xi),…,直到i=n为止。
在回溯法中,上述引入的树被称为问题P的状态空间树;树T上任意一个结点被称为问题P的状态结点;树T上的任意一个叶子结点被称为问题P的一个解状态结点;树T上满足约束集D的全部约束的任意一个叶子结点被称为问题P的一个回答状态结点,它对应于问题P的一个解。
穷举法
顾名思义,穷举法就是通过把需要解决问题的所有可能情况逐一试验来找出符合条件的解的方法,对于许多毫无规律的问题而言,穷举法用时间上的牺牲换来了解的全面性保证,尤其是随着计算机运算速度的飞速发展,穷举法的形象已经不再是最低等和原始的无奈之举,比如经常有黑客在几乎没有任何已知信息的情况下利用穷举法来破译密码,足见这种方法还是有其适用的领域的。可是,在实际生活中,只有很少的一些问题是真正意义上的“毫无规律”,其余的大多数仍有内在规律可循,对于这些问题,使用穷举法在效率上就显得比较低下,而在一些对速度要求较高的区域和规模较大的问题上,效率的低下往往是致命的。
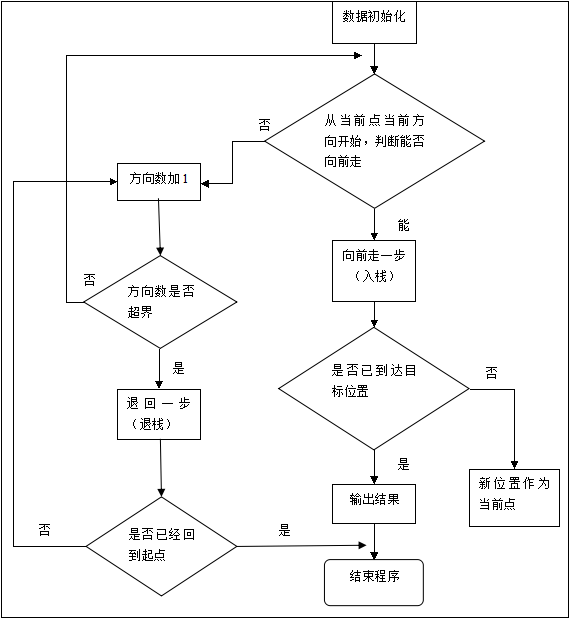
详细流程图
图3-3 解决八皇后问题的基本流程图
5.调试分析
1)运行时有些函数的头文件未定义,导致无法进行编译;而且在调试时有些头文件的使用范畴弄混淆了;
2)开始编第一种方法(递归回溯)时,for与if的循环嵌套未能很好掌握,导致几次调试都出现比较严重的错误;且在运用该方法时,未能将八皇后问题的具体思路搞清,没有考虑“如果前次的皇后放置导致后面的放置无论如何都不能满足要求”的问题;
3)在统计方法的个数时,未将累加的那个整型变量进行初始化,导致无法显示,八皇后摆放的是“第X种情况”,也无法统计出八皇后的排列方式是否一定是92种情况。
4)在第三种方法(穷举)编译时,开始我把二维数组定义成整型,但其后在输出棋盘格式时,更本无法调试成功,出现了类型之间的冲突,因为在输出时,我又给那二维数组付成了字符型;
5)未用setw( )函数时,显示的结果相当难看,所定义的标志符都紧靠在一起;多加了一个换行符后,各种情况的间距增大,阅读时舒服多了;
6)如果将92种情形全部打印,则前面的几十种情况将无法显示出,要想看到前面的状态,必须添加一个控制语句,使其能一个一个的输出。
6.测试结果
开始运行界面,如图6-1所示
输入1时,按enter后如图 6-2所示;
输入2时,按enter后如图6-3所示;
输入3时,按enter后如图6-4所示。
输入0时,按enter后如图6-5所示。
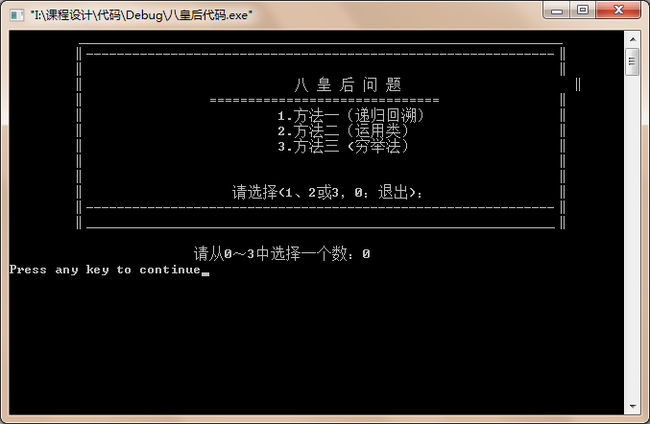
图6-1 八皇后运行界面
(这是把皇后程序进入后的欢迎界面,使用者可以根据需要,选择1,2,3或者0来进行相应的活动)
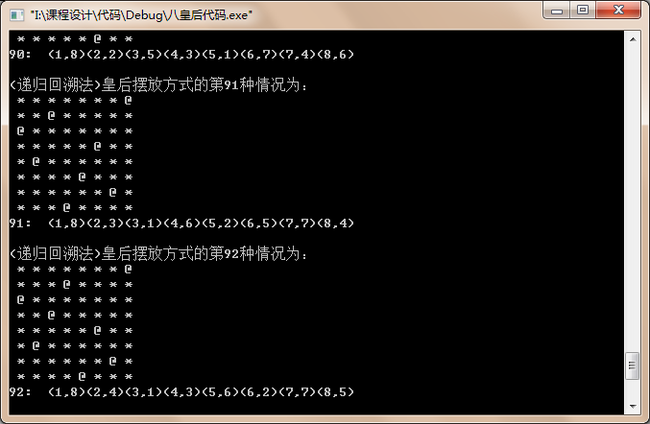
图 6-2 递归回溯法界面
(这是把皇后第一种方法运行后显示的界面,其中*是棋盘中棋子的位置,@是棋盘中皇后的位置,坐标表示在当前情况下皇后所处位置)
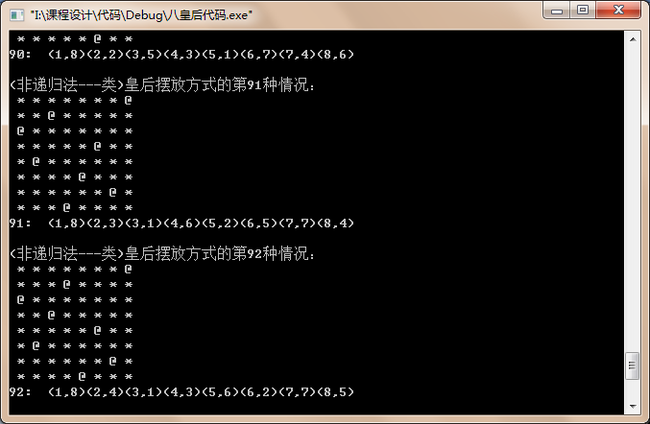
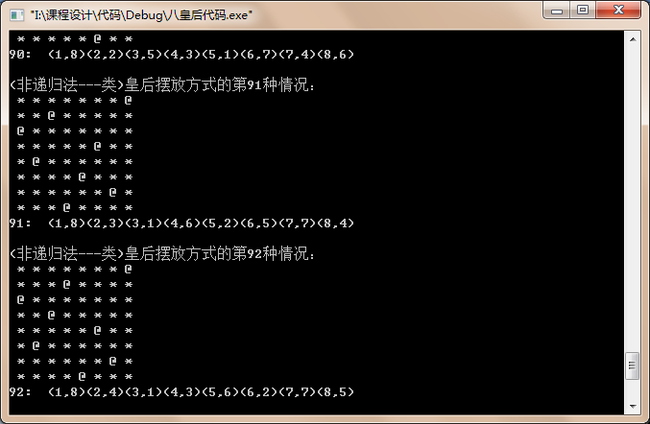
图6-3 非递归界面
(这是把皇后第二种方法运行后显示的界面,其中*是棋盘中棋子的位置,@是棋盘中皇后的位置,坐标表示在当前情况下皇后所处位置)
图6-4 穷举递归法界面
(这是把皇后第三种方法运行后显示的界面,其中*是棋盘中棋子的位置,@是棋盘中皇后的位置,坐标表示在当前情况下皇后所处位置)
7、完整代码
include<iostream.h>//数据流输入/输出
#include<iomanip.h>//参数化输入/输出
#include<stdlib.h>//定义杂项函数及内存分配函数
#include<stdio.h>//定义输入/输出函数
/*------------------------------------------------------*/
/*--------------方法一:递归法--------------------------*/
/*------------------------------------------------------*/
// static: 避免命名有冲突
//棋盘初始化时,空格的地方为*,放置皇后的地方为@
static char Queen[8][8];
static int a[8]; //数组a[i]:a[i]表示第i个皇后放置的列,i的范围:----8
static int b[15]; //主对角线数组
static int c[15]; //从对角线数组,根据程序的运行,去决定主从对角线是否放入皇后
static int iQueenNum=0; //记录总的棋盘状态数
static int iNum=1;
void iQueen(int i); //参数i代表行
void measure1()
{
int iLine; //横行
int iColumn; //纵行
for(iLine=0;iLine<8;iLine++)
{
a[iLine]=0; //列标记初始化,表示无列冲突
for(iColumn=0;iColumn<8;iColumn++)
Queen[iLine][iColumn]='*';
}
for(iLine=0;iLine<15;iLine++) //主、从对角线标记初始化,表示没有冲突
b[iLine]=c[iLine]=0;
iQueen(0);
};
void iQueen(int i) //i为当前处理的行
{
int iColumn;
for(iColumn=0;iColumn<8;iColumn++)
{
if(a[iColumn]==0&&b[i-iColumn+7]==0&&c[i+iColumn]==0) //如果无冲突
{
Queen[i][iColumn]='@'; //放皇后
a[iColumn]=1; //标记,下一次该列上不能放皇后
b[i-iColumn+7]=1; //标记,下一次该主对角线上不能放皇后
c[i+iColumn]=1; //标记,下一次该从对角线上不能放皇后
if(i<7)
iQueen(i+1); //如果行还没有遍历(沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问)完,进入下一行
else //否则输出
{
int iLine; //输出棋盘状态
int iColumn;
cout<<"(递归法)皇后摆放方式的第"<<iNum<<"种情况为:"<<endl;
for(iLine=0;iLine<8;iLine++)
{
for(iColumn=0;iColumn<8;iColumn++)
cout<<setw(2)<<Queen[iLine][iColumn];
cout<<endl;
}
cout<<iNum<<": ";
for(iLine=0;iLine<8;iLine++)
{
for(iColumn=0;iColumn<8;iColumn++)
{
if(Queen[iLine][iColumn]=='@')
cout<<"("<<iLine+1<<','<<iColumn+1<<")";
}
}
cout<<endl;
system("pause>nul"); //从程序里调用pause命令,一个结果一个结果地看
iNum++;
cout<<endl;
}
//如果前次的皇后放置导致后面的放置无论如何都不能满足要求,则回溯,重新标记
Queen[i][iColumn]='*';
a[iColumn]=0;
b[i-iColumn+7]=0;
c[i+iColumn]=0;
}// if ends
}
}
/*----------------------------------------------------------*/
/*----------------------方法二:运用类----------------------*/
/*----------------------------------------------------------*/
//自定义一个类:CQueen
class cQueen {
int aQueen[8]; //可以在类外访问的私有成员(默认)
int sum;
public: //只能被该类的成员函数所访问的公有成员
cQueen(); //构造函数:确保每个对象正确地初始化
int judge(int x,int y);
void show();
void step();
};
cQueen::cQueen()//通过构造函数对aQueen[1---8]初始化
{
sum=0;
for(int i=0;i<8;i++)
aQueen[i]=0;
}
int cQueen::judge(int x,int y) //判断皇后摆放位置是否有冲突,如果没有冲突,则返回;如果有冲突,则返回
{
for(int i=0;i<x;i++)
if(aQueen[i]==y || aQueen[i]+x-i==y || aQueen[i]-x+i==y)
return 0;
return 1;
}
void cQueen::step() //一步一步进行查找摆放
{
int x=0,y=0;//标记皇后所在键盘位置,x代表列,y代表行(相当于坐标)
while(aQueen[0]<8)
{
while(y<8)
{
if(judge(x,y)) //调用类函数judge(x,y),如果aQueen[1---8]都已经标记,则执行该语句
{
aQueen[x]=y; //摆放皇后
x++; //进行下一列时
y=0; //y进行重置
}
else //否则,进入下一行
y++;
} //当执行到最后一行时,继续执行下一个if语句
if(y==8&&x!=8) //最后一行,从第一列开始
{
if(aQueen[--x]!=7)
y=++aQueen[x];
else if(aQueen[0]!=7)
y=++aQueen[--x];
else
aQueen[0]=8;
}
if(x==8) //最后一列
{
show(); //x,y从至结束,大循环结束
if(aQueen[--x]!=7)
y=++aQueen[x];
else
y=++aQueen[--x];
}
}
}
void cQueen::show()//输出棋盘状态
{
cout<<"(非递归法)皇后摆放方式的第"<<++sum<<"种情况:"<<endl;
for(int i=0;i<8;i++) //输出八皇后的各种状态,有皇后的位置用@ 表示,没有皇后的位置用* 表示
{
for(int j=0;j<aQueen[i];j++)
cout<<setw(2)<<"*";
cout<<setw(2)<<"@";
for(j++;j<8;j++)
cout<<setw(2)<<"*";
cout<<endl;
}
cout<<sum<<": ";
for(int k=0;k<8;k++)
cout<<'('<<k+1<<','<<aQueen[k]+1<<")";
cout<<endl<<endl;
// system("pause");//从程序里调用pause命令,一个结果一个结果地看
}
void measure2()
{
cQueen a;
a.step();
}
/*--------------------------------------------------------------*/
/*------------------方法三:穷举法---------------------------*/
/*--------------------------------------------------------------*/
//使用优化后的穷举法,用递归实现N层穷举,每调用一次穷举函数则穷举一列
const int LINE=8;//const定义整新型常量LINE和ROW(8*8的棋盘)
const int ROW=8;
void queen(int row,int rec[]);//row为当前穷举的列,rec[]记录已穷举的信息,rec[3]=2代表(3,2)已放下棋子
bool isqueen(int i,int rec[],int row);//判断当前i是否与已放下的棋子能相互攻击
void printqueen(int rec[]);//输出符合条件的棋子摆放方式
void measure3()
{
int rec[9]={0};//记录穷举信息数组
queen(1,rec);//执行八皇后
system("pause");
}
void queen(int row,int rec[])//八皇后函数
{
int tmprec[ROW+1]={0};
//向下一列穷举传递信息时使用tmprec,不丢失rec的记录
for(int i=1;i<=row;i++) tmprec[i]=rec[i];//复制数组
if (row!=ROW)//不是最后一列时(第ROW列即为最后一列)
{
for (i=1;i<=ROW;i++)
{
if(isqueen(i,rec,row)) //i与已放下的棋子不能相互攻击时
{
tmprec[row]=i;
queen(row+1,tmprec);//继续穷举下一列
}
}
}
else//最后一列时
for (i=1;i<=ROW;i++)
if(isqueen(i,rec,row))//i与已放下的棋子不能相互攻击时
{
tmprec[row]=i;
printqueen(tmprec);//输出符合条件的棋子摆放方式
}
}
bool isqueen(int i,int rec[],int row)//判断当前i是否与已放下的棋子能相互攻击
{//(row,i)即是此次穷举出来的棋子的坐标
if (row==1) return 1;//第一列
for(int j=1;j<row;j++)
{
if(rec[j]==i||rec[j]==i+row-j||rec[j]==i-row+j)//如果(有棋子在同一直线||有棋子在同一斜线)
return 0;
}
return 1;
}
void printqueen(int rec[])//输出符合条件的棋子摆放方式
{
char q[LINE+1][ROW+1]={'0'};
static int num=1;//记录已输出符合条件的棋盘数量
for (int i=1;i<=LINE;i++)
{
for (int j=1;j<=ROW;j++)
{
if(rec[i]!=j)
q[i][j]='*';
else
q[i][j]='@';
}
}
//将一维记录转换成LINE*ROW的矩阵,方便打印
cout<<"(穷举法)皇后摆放方式第"<<num<<"种情况:"<<endl;//输出数量
for (i=1;i<=ROW;i++)
{
for (int j=1;j<=ROW;j++)
cout<<setw(2)<<q[i][j];
cout<<endl;
}
cout<<num<<": ";
for (i=1;i<=ROW;i++)
{
for (int j=1;j<=ROW;j++)
if (rec[i]==j)
cout<<"("<<i<<','<<j<<")";
}
cout<<endl<<endl;
num++;
// system("pause");
}
void menu() //输出界面
{
cout<<"\t"<<" _________________________________________ "<<endl;
cout<<"\t"<<"‖----------------------------------------‖"<<endl;
cout<<"\t"<<"‖ ‖"<<endl;
cout<<"\t"<<"‖ 八皇后问题 ‖"<<endl;
cout<<"\t"<<"‖ ==================== ‖"<<endl;
cout<<"\t"<<"‖ 1.方法一: 递归法 ‖"<<endl;
cout<<"\t"<<"‖ 2.方法二: 运用类 ‖"<<endl;
cout<<"\t"<<"‖ 3.方法三: 穷举法 ‖"<<endl;
cout<<"\t"<<"‖ 0.后退 ‖"<<endl;
cout<<"\t"<<"‖ ‖"<<endl;
cout<<"\t"<<"‖ 请选择(1、2,或者0): ‖"<<endl;
cout<<"\t"<<"‖----------------------------------------‖"<<endl;
cout<<"\t"<<"‖________________________________________‖"<<endl;
}
int main()//主函数
{
for(;;)
{
menu();
cout<<endl;
cout<<"\t\t\t请从~中选择一个数:";
int number;
cin>>number;
switch(number)
{
case 1: measure1();break;
case 2: measure2();break;
case 3: measure3();break;
case 0: return 0;
default:
cout<<"抱歉,没有该选项,请重新作出选择!!"<<endl;
}
}
return 0;
}
8总结及体会。
就编写的程序而言,虽然能达到预期的结果,但在运行时所需的时间比较长,而且总体结构还不够简洁,不太容易去理解。许多问题还需要继续研究,许多技术还需要更多的改进。去图书馆借了不少书,也去网上看了些资料,只是对大概的知识有了点了解,但还是很难着手于写代码,后来就按照老师说的,先搞清楚原理,再考虑如何去实现!后来又去上网查看相关资料,又到图书馆借了很多书看,总算有头绪了。但在调试过程中,还是遇到了很多困难,后来通过了很多同的帮助才把问题解决了。
通过这次的课程设计,让我了解了八皇后这一经典的问题。同时让我更好地掌握了栈思想以及一维数组等等知识,以及一些书本上没有的东西,这对我以后的学习生涯以及将来步入社会起到很大的帮助。这次课程设计虽然花了我很多时间和精力,但很值得,因为它对我能力提高起到很大帮助。这次课程设计也提醒我以前知识的匮乏,它给我敲响了警钟,让我意识到自己基础的不扎实.当然这次实验还是有很多问题的。比如程序设计的界面不够好,一些程序并非自己所写,而是修改某些程序而成,但这些不该,在下次课程设计时不会再发生.
在编写代码时,我希望能随机选择一数 X(1~92)后,能输出该种情况所对应的八个皇后的摆放方式和每个皇后所在的位置,但想了好久,就是无法实现。而且,当92种情况都输出时,前面的几十种情况无法看到,要想让摆放皇后的图形和所在具体的位置一起输出,就得修改程序让使她们一个一个地输出,这样显然比较麻烦。
针对八皇后这个课题,也许表层只局限于对八个皇后的摆放,但还可以对更多的情况进行探讨分析,比如九皇后,十皇后等等。在报告正文中已经多次提到关于N皇后的设计方法,但只是一带而过,有些问题很难通过一个报告设计就轻而易举的得到解决,还需要花费更多的时间。也许随着皇后个数的增多,程序运行的时间将变得很长,我们能否将运行的时间缩短呢?
一周的努力过后,也算是颇有收获,很多以前不清楚、不熟悉的内容都在这一周的努力中得到了锻炼,感谢老师给予的大量帮助及指导,感谢同学们的帮助,才让我顺利完成了这次的课程设计!通过他们们的帮助,我深刻体会到:做程序设计需要团队共同努力,共同贡献自己的力量,才能编写出一段好的程序,谢谢你们!
图6-4 退出界面