顺序栈求解迷宫问题
下图所示的迷宫,从(1,1)走到(8,8)
int mg[10][10] = { //迷宫
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 0, 0, 1, 0, 0, 0, 1, 0, 1},
{1, 0, 0, 1, 0, 0, 0, 1, 0, 1},
{1, 0, 0, 0, 0, 1, 1, 0, 0, 1},
{1, 0, 1, 1, 1, 0, 0, 0, 0, 1},
{1, 0, 0, 0, 1, 0, 0, 0, 0, 1},
{1, 0, 1, 0, 0, 0, 1, 0, 0, 1},
{1, 0, 1, 1, 1, 0, 1, 1, 0, 1},
{1, 1, 0, 0, 0, 0, 0, 0, 0, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1}
};迷宫用二位数组表示,0表示可以通过的块,1表示不可以通过的块。
大致思路:
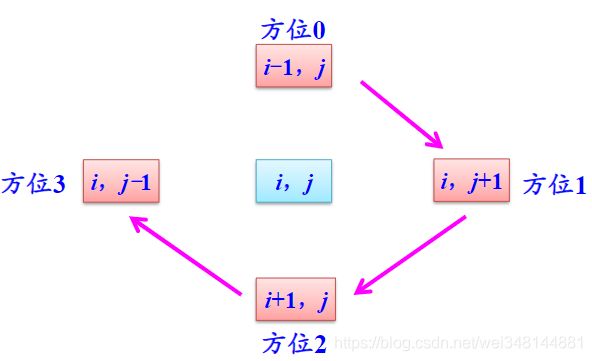
定义一个栈,栈元素包括路径的坐标(x,y)、(x,y)的扫描记录(di)和栈顶(top)三个变量。di用来标记当前位置的上下左右四个位置,如下图,最上边方位0是di=0,右边方位1是di=1...也就是说,每次扫描从di=0开始,如果扫描到该方位的坐标点为0(可以通过的块),先将该点入栈,再移动到扫描到的那个点!注意这是上一个点的di值被入栈了,也就是保留了扫描记录,如果回到了该点,就会接着扫描纪录继续扫描,而不会重新扫描进而导致重走老路,这一点很重要。还要注意的是入栈的坐标点都要将其坐标改为一个非0的值(当然也不能是1)以标记该点是来的路径上的点,如果入栈的点没被标记还是0的话,那该点可能被扫描到而误以为是一个出口而折返回去。另一方面,退栈的时候,退栈的点要被恢复为0(清除标记),这是为了不影响其他路径!
代码
#include
#include
#include
int mg[10][10] = { //迷宫
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 0, 0, 1, 0, 0, 0, 1, 0, 1},
{1, 0, 0, 1, 0, 0, 0, 1, 0, 1},
{1, 0, 0, 0, 0, 1, 1, 0, 0, 1},
{1, 0, 1, 1, 1, 0, 0, 0, 0, 1},
{1, 0, 0, 0, 1, 0, 0, 0, 0, 1},
{1, 0, 1, 0, 0, 0, 1, 0, 0, 1},
{1, 0, 1, 1, 1, 0, 1, 1, 0, 1},
{1, 1, 0, 0, 0, 0, 0, 0, 0, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1}
};
typedef struct { //表示当前位置和可走的方位
int i;
int j;
int di;
}Box;
typedef struct { //顺序栈
Box data[Maxsize];
int top;
}StType;
bool magpath(int xi,int yi,int xe,int ye)//起点xi,yi 终点xe,ye
{
int i, j, di, find;
int k;
StType st;
st.top = -1; //栈顶
st.top++;
st.data[st.top].i = xi;
st.data[st.top].j = yi;
st.data[st.top].di = -1;//先将起始位置标记入栈
mg[xi][yi] = -1;//当前点都进行标记
while (st.top>-1)//如果不通就会原路返回,如果所有的路都不通就会返回到起点。也就是说只要是栈里有数据,就说明还没回到原点。
{
i = st.data[st.top].i;
j = st.data[st.top].j;
di = st.data[st.top].di;
if (i == xe && j == xe) //找到出口了
{
for (k = 0; k <= st.top; k++)
{
printf("(%d,%d)\n",st.data[k].i, st.data[k].j);//输出路径
}
return true;
}
find = 0;//还没找到出口
while (di<4 && find == 0) //扫描附近可走的点,找到就退出循环,或者没找到也退出循环。
{
di++; //加一
switch (di) //根据方位号di映射到坐标,可以修改这里来改变搜索的优先级,也就是路径选择的优先级
{
case(0):i = st.data[st.top].i -1; j = st.data[st.top].j; break;
case(1):i = st.data[st.top].i; j = st.data[st.top].j -1; break;
case(2):i = st.data[st.top].i + 1; j = st.data[st.top].j; break;
case(3):i = st.data[st.top].i; j = st.data[st.top].j + 1; break;
}
if (mg[i][j] == 0)find = 1;//找到可以走的点。
}//找出口
if (find)//找到出口了
{
st.data[st.top].di = di;//保存原栈顶元素的di值,di值以内的都是不能走已经或者走过的点,如果下次退到该点,就不会走老路了。
//入栈
st.top++;
st.data[st.top].i = i; st.data[st.top].j = j;//记录出口坐标
st.data[st.top].di = -1;//来到新的点,di为-1
mg[i][j] = -1;//标记路径
}
else //找遍了都没找到出口,就得退栈
{
mg[st.data[st.top].i][st.data[st.top].j] = 0;//抹掉痕迹,允许其他路径通过。
st.top--;
}
}
return false;//都没找到
}
int main()
{
if(magpath(1,1,8,8))printf("true");
return 0;
} 这个路径真的是....太垃圾了。后边再优化。