LeetCode 第250场周赛(分情况dp,离线查询,01字典树)
第250场周赛
将近700名,还是两道的水平,第三道想了一个多小时没想出来…难受,还是菜
5161. 可以输入的最大单词数
题目描述
键盘出现了一些故障,有些字母键无法正常工作。而键盘上所有其他键都能够正常工作。
给你一个由若干单词组成的字符串 text ,单词间由单个空格组成(不含前导和尾随空格);另有一个字符串 brokenLetters ,由所有已损坏的不同字母键组成,返回你可以使用此键盘完全输入的 text 中单词的数目。
示例 1:
输入:text = “hello world”, brokenLetters = “ad”
输出:1
解释:无法输入 “world” ,因为字母键 ‘d’ 已损坏。
示例 2:
输入:text = “leet code”, brokenLetters = “lt”
输出:1
解释:无法输入 “leet” ,因为字母键 ‘l’ 和 ‘t’ 已损坏。
示例 3:
输入:text = “leet code”, brokenLetters = “e”
输出:0
解释:无法输入任何单词,因为字母键 ‘e’ 已损坏。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/maximum-number-of-words-you-can-type
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
先用一个哈希表存储坏了的字母,然后查看每个单词中是否有这个字母
class Solution {
public int canBeTypedWords(String text, String brokenLetters) {
String[] ss = text.split(" ");
int l = ss.length;
int res = 0;
boolean[] used = new boolean[26];
for(int i = 0; i < brokenLetters.length(); i++){
used[brokenLetters.charAt(i) - 'a'] = true;
}
for(int i = 0; i < l; i++){
String s = ss[i];
boolean flag = true;
for(int j = 0; j < s.length(); j++){
if(used[s.charAt(j) - 'a']){
flag = false;
break;
}
}
if(flag)
res++;
}
return res;
}
}
5814. 新增的最少台阶数
题目描述
给你一个 严格递增 的整数数组 rungs ,用于表示梯子上每一台阶的 高度 。当前你正站在高度为 0 的地板上,并打算爬到最后一个台阶。
另给你一个整数 dist 。每次移动中,你可以到达下一个距离你当前位置(地板或台阶)不超过 dist 高度的台阶。当然,你也可以在任何正 整数 高度处插入尚不存在的新台阶。
返回爬到最后一阶时必须添加到梯子上的 最少 台阶数。
示例 1:
输入:rungs = [1,3,5,10], dist = 2
输出:2
解释:
现在无法到达最后一阶。
在高度为 7 和 8 的位置增设新的台阶,以爬上梯子。
梯子在高度为 [1,3,5,7,8,10] 的位置上有台阶。
示例 2:
输入:rungs = [3,6,8,10], dist = 3
输出:0
解释:
这个梯子无需增设新台阶也可以爬上去。
示例 3:
输入:rungs = [3,4,6,7], dist = 2
输出:1
解释:
现在无法从地板到达梯子的第一阶。
在高度为 1 的位置增设新的台阶,以爬上梯子。
梯子在高度为 [1,3,4,6,7] 的位置上有台阶。
示例 4:
输入:rungs = [5], dist = 10
输出:0
解释:这个梯子无需增设新台阶也可以爬上去。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/add-minimum-number-of-rungs
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
看到以后,第一反应,如果两个台阶高度相差大于dist就需要加台阶,然后就看加多少个台阶,恰好等于不要加,也可以用diff - 1来当被除数代替分情况讨论
为什么
class Solution {
public int addRungs(int[] rungs, int dist) {
int res = 0;
int pre = 0;
int l = rungs.length;
for(int i = 0; i < l; i++){
int temp = rungs[i];
int diff = temp - pre;
int t = diff / dist;
if(t * dist == diff)
res += t - 1;
else
res += t;
pre = temp;
}
return res;
}
}
5815. 扣分后的最大得分(dp)
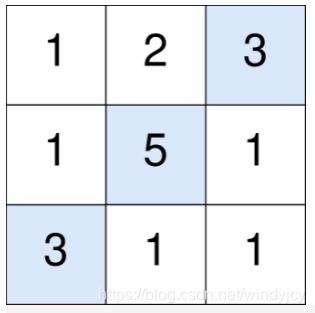
给你一个 m x n 的整数矩阵 points (下标从 0 开始)。一开始你的得分为 0 ,你想最大化从矩阵中得到的分数。
你的得分方式为:每一行 中选取一个格子,选中坐标为 (r, c) 的格子会给你的总得分 增加 points[r][c] 。
然而,相邻行之间被选中的格子如果隔得太远,你会失去一些得分。对于相邻行 r 和 r + 1 (其中 0 <= r < m - 1),选中坐标为 (r, c1) 和 (r + 1, c2) 的格子,你的总得分 减少 abs(c1 - c2) 。
请你返回你能得到的 最大 得分。
abs(x) 定义为:
如果 x >= 0 ,那么值为 x 。
如果 x < 0 ,那么值为 -x 。
示例 1:
输入:points = [[1,2,3],[1,5,1],[3,1,1]]
输出:9
解释:
蓝色格子是最优方案选中的格子,坐标分别为 (0, 2),(1, 1) 和 (2, 0) 。
你的总得分增加 3 + 5 + 3 = 11 。
但是你的总得分需要扣除 abs(2 - 1) + abs(1 - 0) = 2 。
你的最终得分为 11 - 2 = 9 。
示例 2:
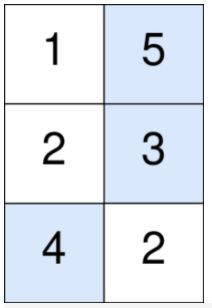
输入:points = [[1,5],[2,3],[4,2]]
输出:11
解释:
蓝色格子是最优方案选中的格子,坐标分别为 (0, 1),(1, 1) 和 (2, 0) 。
你的总得分增加 5 + 3 + 4 = 12 。
但是你的总得分需要扣除 abs(1 - 1) + abs(1 - 0) = 1 。
你的最终得分为 12 - 1 = 11 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/maximum-number-of-points-with-cost
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
写了个暴力解法,然后不出意外超时了,就卡在最后一个用例上。做题的时候刚开始还头脑清晰,后面越想脑子越乱
一直在想一个问题,就是知道了上一行每一个位置对应的最大值,那么下一行的最大值该怎么求
然后很自然的想到是否能利用到前面的值,因为很显然看时间复杂度,最多只能有两层循环。
然后冥冥中感觉是这样做,但是就是想不明白,比赛完看第五名大佬的写法(因为是java的),发现从左到右一次,从右到左一次,还是没看明白。。
看了一下赞多的解答,醍醐灌顶
暴力解法对应的转移方程如下(max是遍历上一行所有值的max)
dp[i][j] = point[i][j] + max(dp[i - 1][k] + |j - k|)
然后将绝对值符号去掉的话,可以得到:
dp[i][j] = if k < j, point[i][j] + max(dp[i - 1][k] + j - k) else if k >= j, point[i][j] + max(dp[i - 1][k] + k - j)
然后将 j 提出来
dp[i][j] = if k < j, point[i][j] + j + max(dp[i - 1][k] - k) else if k >= j, point[i][j] - j + max(dp[i - 1][k] + k)
这样写了以后,对于当前位置 j ,需要知道它左边部分的最大值,那就从左到右遍历,此时 k 是小于 j 的,记录一个当前的最大值,存储在一个数组中,然后就能在O(n)的求出每个位置前半部分的值
然后再从右向左遍历,记录后半部分的值
最后,dp[i][j] 的值根据式子,就可以求出来了
暴力解
class Solution {
public long maxPoints(int[][] points) {
int m = points.length;
int n = points[0].length;
long[] row = new long[n];
for(int i = 0; i < n; i++){
row[i] = points[0][i];
}
//优化
for(int i = 1; i < m; i++){
long[] te = Arrays.copyOf(row, n);
for(int j = 0; j < n; j++){
for(int k = 0; k < n; k++){
row[j] = Math.max(row[j], te[k] + points[i][j] - Math.abs(k - j));
}
}
}
long res = 0;
for(int i = 0; i < n; i++){
res = Math.max(res, row[i]);
}
return res;
}
}
根据我的理解写一下代码:
写出来一个这样的代码,关键点还是在left和right数组的计算。
这里是什么意思呢,比如left数组,求的是 max(dp[i - 1][k] + j - k),当前位置的最大值就是之前之前的最大值减1和当前位置值相比较,为什么要减1呢,因为每向右移动一位,那么leftmax必然会少1
同理right数组也是这样求出来的
求出这两个数组以后,当前位置左边的最大值和右边的最大值就知道了,然后再取个最大就是当前位置的值dp[i][j]
class Solution {
public long maxPoints(int[][] points) {
int m = points.length;
int n = points[0].length;
long[][] dp = new long[m][n];
//初始化
for(int i = 0; i < n; i++){
dp[0][i] = points[0][i];
}
//状态转移
for(int i = 1; i < m; i++){
//从左到右,k < j,求 max(dp[i - 1][k] + j - k)
long leftmax = Long.MIN_VALUE + 1;
long[] left = new long[n];
for(int j = 0; j < n; j++){
//每次向右移动,都要leftmax都要减1,然后和当前正下方的值相比较
leftmax = Math.max(leftmax - 1, dp[i - 1][j]);
left[j] = leftmax;
}
//从右向左,求 max(dp[i - 1][k] + k - j)
long rightmax = Long.MIN_VALUE + 1;
long[] right = new long[n];
for(int j = n - 1; j >= 0; j--){
//每次向左移动,都要rightmax都要减1,然后和当前正下方的值相比较
rightmax = Math.max(rightmax - 1, dp[i - 1][j]);
right[j] = rightmax;
}
for(int j = 0; j < n; j++){
dp[i][j] = Math.max(left[j], right[j]) + points[i][j];
}
}
long res = 0;
for(int i = 0; i < n; i++){
res = Math.max(res, dp[m - 1][i]);
}
return res;
//直接转换成流的形式
// return Arrays.stream(dp).max().getAsLong();
}
}
最后想想这道题到底有什么样的启发,这种动态规划第一次见。首先,根据绝对值,把情况分成两种。当看到k= < j 和 k >= j 时,就可以比较容易的想到从两边分别遍历,求出两边的最大值,然后再对两个最大值求最大
能得到的启发就是遇到这种分情况的问题,要拆分来考虑,分成子问题以后,往往能够得到简化
最后,因为最近看了stream的知识, 学习一下stream的用法
421. 数组中两个数的最大异或值(字典树)
由于最后一题的需要,这里先看一下这道题
题目描述
给你一个整数数组 nums ,返回 nums[i] XOR nums[j] 的最大运算结果,其中 0 ≤ i ≤ j < n 。
进阶:你可以在 O(n) 的时间解决这个问题吗?
示例 1:
输入:nums = [3,10,5,25,2,8]
输出:28
解释:最大运算结果是 5 XOR 25 = 28.
示例 2:
输入:nums = [0]
输出:0
示例 3:
输入:nums = [2,4]
输出:6
示例 4:
输入:nums = [8,10,2]
输出:10
示例 5:
输入:nums = [14,70,53,83,49,91,36,80,92,51,66,70]
输出:127
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/maximum-xor-of-two-numbers-in-an-array
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
有一天的每日一题,用字典树做
求异或值,可以将一个数表示成31个二进制位的形式,然后根据数组中的所有数,每一位是0或者1,构建一个字典树。
然后怎么求两个数的最大异或值呢,已知一个数为t,就是从根节点开始往下进行选择,如果存在和t当前位相反的节点,那么就走这个节点,不存在就走同样的节点。最后走到树的叶子部分,得到的值就是异或能得到的最大值
在具体实现过程中,没有必要先构建树,可以边遍历边构建字典树,然后记录当前的最大值
自己再写一遍,加深印象:
class Solution {
Trie trie = new Trie();
public int findMaximumXOR(int[] nums) {
int l = nums.length;
int res = 0;
for(int i = 1; i < l; i++){
//把前一个节点加到字典树中
add(nums[i - 1]);
int t = check(nums[i]);
res = Math.max(res, t);
}
return res;
}
public void add(int num){
Trie temp = trie;
for(int i = 30; i >= 0; i--){
int t = ((num >> i) & 1);
if(t == 0){
if(temp.left == null){
temp.left = new Trie();
}
temp = temp.left;
}else{
if(temp.right == null){
temp.right = new Trie();
}
temp = temp.right;
}
}
}
public int check(int num){
Trie temp = trie;
int ret = 0;
for(int i = 30; i >= 0; i--){
int t = ((num >> i) & 1);
if(t == 0){
if(temp.right == null){
temp = temp.left;
ret = (ret << 1) + 0;
}else{
temp = temp.right;
ret = (ret << 1) + 1;
}
}else{
if(temp.left == null){
temp = temp.right;
ret = (ret << 1) + 0;
}else{
temp = temp.left;
ret = (ret << 1) + 1;
}
}
}
return ret;
}
}
class Trie{
Trie left;
Trie right;
}
5816. 查询最大基因差(字典树+离线查询)
题目描述
给你一棵 n 个节点的有根树,节点编号从 0 到 n - 1 。每个节点的编号表示这个节点的 独一无二的基因值 (也就是说节点 x 的基因值为 x)。两个基因值的 基因差 是两者的 异或和 。给你整数数组 parents ,其中 parents[i] 是节点 i 的父节点。如果节点 x 是树的 根 ,那么 parents[x] == -1 。
给你查询数组 queries ,其中 queries[i] = [nodei, vali] 。对于查询 i ,请你找到 vali 和 pi 的 最大基因差 ,其中 pi 是节点 nodei 到根之间的任意节点(包含 nodei 和根节点)。更正式的,你想要最大化 vali XOR pi 。
请你返回数组 ans ,其中 ans[i] 是第 i 个查询的答案。
输入:parents = [-1,0,1,1], queries = [[0,2],[3,2],[2,5]]
输出:[2,3,7]
解释:查询数组处理如下:
- [0,2]:最大基因差的对应节点为 0 ,基因差为 2 XOR 0 = 2 。
- [3,2]:最大基因差的对应节点为 1 ,基因差为 2 XOR 1 = 3 。
- [2,5]:最大基因差的对应节点为 2 ,基因差为 5 XOR 2 = 7 。
示例 2:
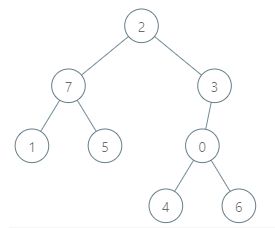
输入:parents = [3,7,-1,2,0,7,0,2], queries = [[4,6],[1,15],[0,5]]
输出:[6,14,7]
解释:查询数组处理如下:
- [4,6]:最大基因差的对应节点为 0 ,基因差为 6 XOR 0 = 6 。
- [1,15]:最大基因差的对应节点为 1 ,基因差为 15 XOR 1 = 14 。
- [0,5]:最大基因差的对应节点为 2 ,基因差为 5 XOR 2 = 7 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/maximum-genetic-difference-query
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
看了下题,然后很自然想到暴力解法,对于要查找的节点,一直向上找,直到根节点,然后求每个节点的异或值的最大者。很显然会超时,不过还是写一下:
class Solution {
public int[] maxGeneticDifference(int[] parents, int[][] queries) {
//暴力
int n = queries.length;
int[] res = new int[n];
//对于每个查询
for(int i = 0; i < n; i++){
int node = queries[i][0];
int val = queries[i][1];
int max = 0;
do{
max = Math.max(max, node ^ val);
node = parents[node];
}while(node != -1);
res[i] = max;
}
return res;
}
}
然后想优化,求两个数最大的异或值,之前每日一题专项训练异或那几天出过
复习过后,再来想这个问题
首先构建字典树,首先将根节点node 的值 i 放在字典树中,然后看有没有点 i 的询问,并处理
然后dfs建树,如果处理完了node的所有子树以后,再将 i 从字典树中删除
为啥要这样做呢,这样做可以保证,当处理到当前节点node时,字典树中只有从根节点root到当前节点node的所有值
根据这个思路,来写一下代码
注意这里的节点删除操作,是在Trie中加了一个成员变量count,定义这个节点出现的次数,如果出现次数为0的话,就相当于删除了这个节点
然后对两个给定的数组,都需要用哈希表预处理,方便查询,否则超时
class Solution {
class Trie{
Trie left;
Trie right;
//考虑到删除操作,就是将这个节点的使用次数-1
int count;
}
Trie trie = new Trie();
int[] parents;
int[][] queries;
int[] res;
Map<Integer, List<Integer>> map = new HashMap<>();
Map<Integer, List<Integer>> node = new HashMap<>();
public int[] maxGeneticDifference(int[] parents, int[][] queries) {
this.parents = parents;
this.queries = queries;
int l = parents.length;
int n = queries.length;
for(int i = 0; i < l; i++){
int val = parents[i];
List<Integer> list = node.getOrDefault(val, new ArrayList<>());
list.add(i);
node.put(val, list);
}
//System.out.println(node.get(0));
for(int i = 0; i < queries.length; i++){
int key = queries[i][0];
int val = queries[i][1];
List<Integer> list = map.getOrDefault(key, new ArrayList<>());
list.add(i);
map.put(key, list);
}
res = new int[n];
//对于每个查询
dfs(-1);
return res;
}
public void dfs(int val){
//先找到当前根节点的子节点
List<Integer> child = node.getOrDefault(val, new ArrayList<>());
//对于每一个子节点
for(int t : child){
//加到字典树中
add(t);
//如果有当前节点的查询
List<Integer> list = map.getOrDefault(t, new ArrayList<>());
for(int j = 0; j < list.size(); j++){
int index = list.get(j);
res[index] = check(queries[index][1]);
}
//然后递归,把子节点加入字典树中
dfs(t);
delete(t);
}
}
public void add(int t){
Trie temp = trie;
temp.count++;
//因为最大2*10^5
for(int i = 17; i >= 0; i--){
int cur = ((t >> i) & 1);
if(cur == 0){
if(temp.left == null)
temp.left = new Trie();
temp = temp.left;
temp.count++;
}else{
if(temp.right == null)
temp.right = new Trie();
temp = temp.right;
temp.count++;
}
}
}
public void delete(int t){
Trie temp = trie;
temp.count--;
//因为最大2*10^5
for(int i = 17; i >= 0; i--){
int cur = ((t >> i) & 1);
if(cur == 0){
temp = temp.left;
temp.count--;
}else{
temp = temp.right;
temp.count--;
}
}
}
public int check(int val){
Trie temp = trie;
int ret = 0;
for(int i = 17; i >= 0; i--){
int cur = ((val >> i) & 1);
if(cur == 0){
if(temp.right == null || temp.right.count == 0){
temp = temp.left;
ret = (ret << 1) + 0;
}else{
temp = temp.right;
ret = (ret << 1) + 1;
}
}else{
if(temp.left == null || temp.left.count == 0){
temp = temp.right;
ret = (ret << 1) + 0;
}else{
temp = temp.left;
ret = (ret << 1) + 1;
}
}
}
return ret;
}
}
这个代码基本上算是一次写成吧,还挺开心的,明显感觉编码能力增强了许多
另外,这个题的还有另一种方法,可持久化字典树+在线查询
什么意思呢,我的理解是这样的,在线查询就是需要能够同时查询多个结果,那么就需要建立持久化的字典树,所以就需要建立出根节点到每一个节点范围内的对应的字典树,然后利用这些字典树进行在线查询。
那么怎么建立这个树呢,除了暴力法,还可以想到的方法就是,每次如果只增加一个数或者减少一个数的时候,并不需要重新建立整个字典树,而是只需要修改字典树中K个节点,就可以得到新状态对应的字典树。先看个思想,具体有题再看吧,今天已经学到很多了