【二叉树相关问题】

一、二叉树的三种遍历方式

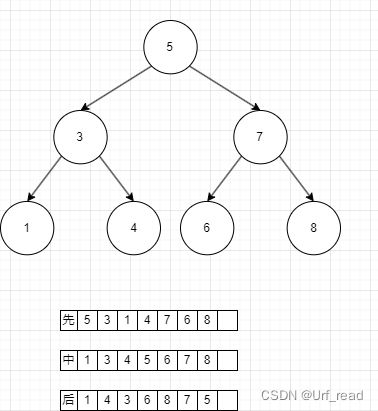
怎么看遍历结果

前中后序遍历，咱先看代码，方便理解

//先序遍历：Preorder Traversal
//中序遍历：Inorder Traversal
//后序遍历：Postorder Traversal
// 前序遍历
public static void preorderTraversal(TreeNode root) {
    if (root == null) {
        return;
    }
    // 访问根节点
    System.out.print(root.val + " ");
    // 递归遍历左子树
    preorderTraversal(root.left);
    // 递归遍历右子树
    preorderTraversal(root.right);
}

// 中序遍历
public static void inorderTraversal(TreeNode root) {
    if (root == null) {
        return;
    }
    // 递归遍历左子树
    inorderTraversal(root.left);
    // 访问根节点
    System.out.print(root.val + " ");
    // 递归遍历右子树
    inorderTraversal(root.right);
}

// 后序遍历
public static void postorderTraversal(TreeNode root) {
    if (root == null) {
        return;
    }
    // 递归遍历左子树
    postorderTraversal(root.left);
    // 递归遍历右子树
    postorderTraversal(root.right);
    // 访问根节点
    System.out.print(root.val + " ");
}

其实先中后说的都是打印“自己”的时机，先序遍历，就是先打印自己的值，然后再去左子树判断，再去右子树。最先打印的一定是头结点。
而中序遍历就是先打印左子树的值，再打印自己的，再去右子树看。
后序遍历，最后打印的是头结点。

二叉树三种遍历方式的参考图↓

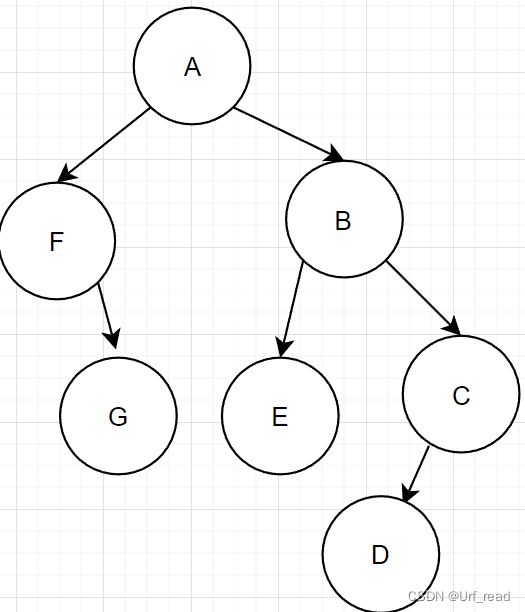
相关题目：已知一颗二叉树的后续遍历序列为：GFEDCBA;中序遍历序列为：FGAEBDC。画出这棵二叉树

思路

1. 首先根据后序遍历的规律——最后打印的为头结点——A

2. 找到A之后，再个根据中序遍历，将中序遍历的序列分为两组。A的左边为左子树，右边为右子树
   

3. 非标准思路：如果手写，到这一步，其实可以先尝试画左子树。尝试着画就行，画出来一个就按照给出的两种遍历序列，自己遍历遍历，看看结果不一样，一样了，就再画下一个结点，不一样了，就再改。

4. 标准思路：递归建树。重复第2步的操作，把中序遍历的序列分为两组之后，[F,G],[E,B,D,C],后序遍历序列去掉已经画好的头结点A，[G,F,E,D,C,B]。再把←这个也分成两组[G,F],[E,D,C,B](分法其实还是看左子树的节点个数，A左边有两个，所以左子树有两个结点）

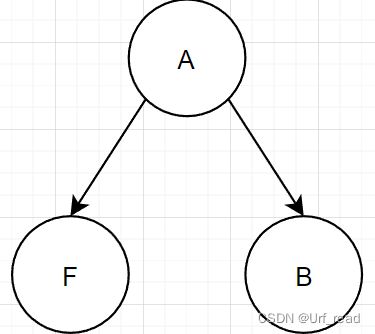
5. 中序[F,G],后序[G,F],假如这也是一个二叉树的遍历结果，画出来它对应的树，你先画出来的不还是头结点F吗？F是后序最后一个，把它接在A的左孩子的位置。接着在去考虑G就好了。（我这里没画出来G，当是练习吧）
   

6. 中序[E,B,D,C],后序[E,D,C,B],这不直接老规矩了都？B是后序最后一个，直接连成A的右孩子。然后再分组就行了
   

7. 去掉已经画好的B，你看中序遍历B左边不就一个E吗？所以中序[E],[D,C]，后序[E],[D,C]。
   

8. 对答案
   

代码版

import java.util.HashMap;
import java.util.Map;

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode(int val) {
        this.val = val;
    }
}

public class BuildTree {
    public static TreeNode buildTree(int[] postorder, int[] inorder) {
        if (postorder == null || postorder.length == 0 || inorder == null || inorder.length == 0) {
            return null;
        }

        Map<Integer, Integer> postIndexMap = new HashMap<>();
        for (int i = 0; i < postorder.length; i++) {
            postIndexMap.put(postorder[i], i);
        }

        return buildTree(postorder, 0, postorder.length - 1, inorder, 0, inorder.length - 1, postIndexMap);
    }

    private static TreeNode buildTree(int[] postorder, int postStart, int postEnd, int[] inorder, int inStart, int inEnd, Map<Integer, Integer> postIndexMap) {
        if (postStart > postEnd || inStart > inEnd) {
            return null;
        }

        int rootVal = postorder[postEnd];
        TreeNode root = new TreeNode(rootVal);

        int rootIndex = postIndexMap.get(rootVal);
        // 计算左子树的节点个数
        int leftSize = searchElement(inorder,rootVal);
        // 递归构建左子树
        root.left = buildTree(postorder, postStart, rootIndex - 1, inorder, inStart, rootIndex - 1, postIndexMap);
        // 递归构建右子树
        root.right = buildTree(postorder, rootIndex + 1, postEnd - 1, inorder, rootIndex + 1, inEnd, postIndexMap);

        return root;
    }    
		//遍历方法可以从上边粘，过来就能用
    public static void main(String[] args) {
        // 后续遍历：4 5 2 6 7 3 1
        int[] postorder = {4, 5, 2, 6, 7, 3, 1};
        // 中序遍历：2 4 5 1 3 6 7
        int[] inorder = {2, 4, 5, 1, 3, 6, 7};

        TreeNode root = buildTree(postorder, inorder);
        System.out.println(root);
    }
    public static int searchElement(int[] array, int target) {
        int left = 0;
        int right = array.length - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (array[mid] == target) {
                return mid;
            } else if (array[mid] < target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        // 元素未找到，返回 -1
        return -1;
    }
}

二、先序线索树

题目：根据先序遍历序列[A,F,G,B,E,C,D]，线索化二叉树。

先序遍历序列：[A,F,G,B,E,C,D]
在先序遍历中，为了提高查找一个元素的前驱、后继的速度，有了线索化这个概念。
如何线索化：左孩子原来为空指前驱，右孩子原来为空指后继。不为空不看，没前驱后继指到空。

例：F的前驱是A，并且F的做指针原来指向空，所以现在指向A。而F原来右指针已经指向了G，不为空，不用考虑。
D左右指针原来都为空，D的前驱为C，所以做指针指向C，D没有后继，所以右指针还为空。

三、二叉树转树、或森林

树转二叉树

一棵树↑
横着，把自己的左孩子和它的兄弟给连起来

只连亲兄弟，F–G就别连了。
然后去掉“多余”的连线，再拉直。
多余的连线,,

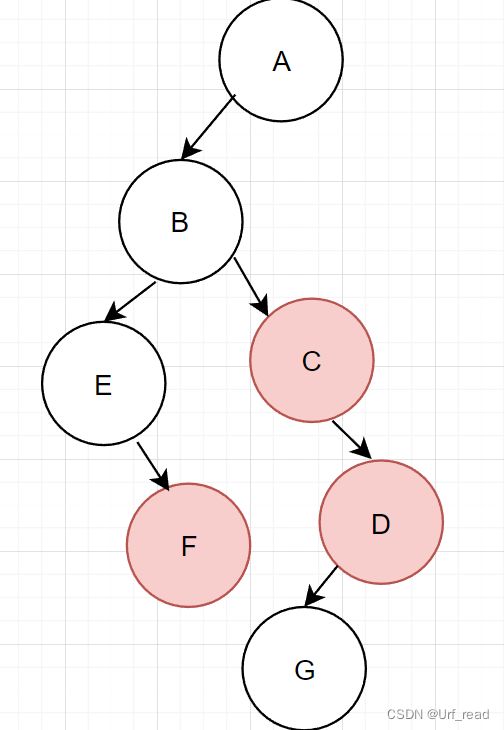
二叉树转树

把红色的这些节点（都是自己父节点的右孩子），“拉上去”

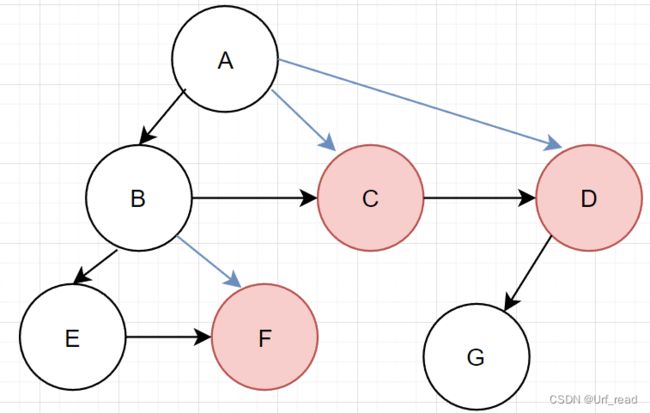
再补上蓝色的边，就是用父节点，连接自己左孩子的兄弟们
删除横这的边

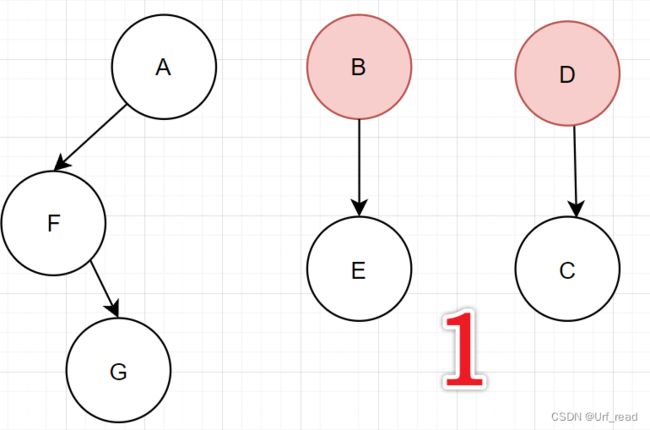
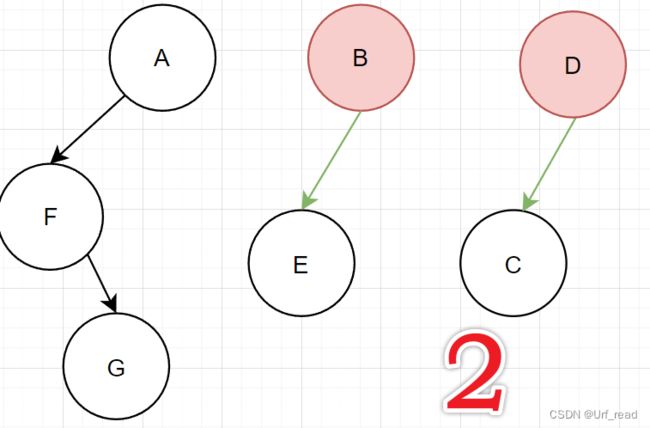
二叉树转森林

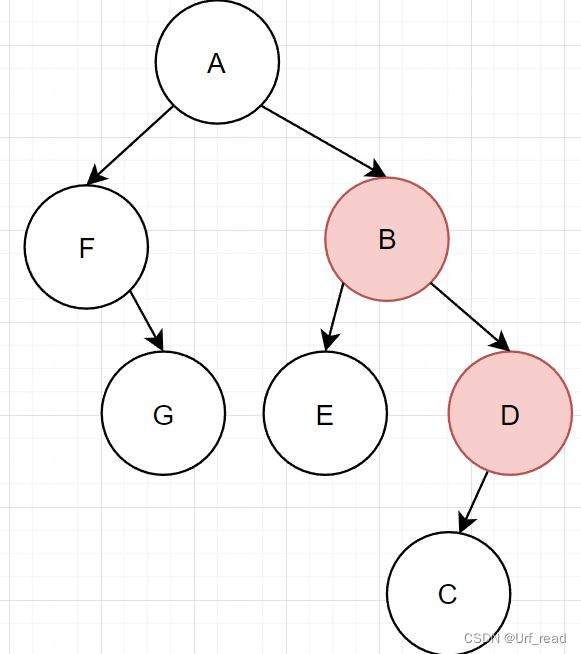
把B和D拉上去，然后去掉横着的边（和转树其实挺像的，看头结点有没有右孩子吧，有了就转成森林了）

森林转二叉树

先把每一棵树都转成二叉树。转完之后头结点肯定没右孩子，有了，你就是没转对。
然后把后面的二叉树，当成第一棵树的右子树加进来

再把连到B的右子树就行了