【论文阅读】Real-time Constrained Cycle Detection in Large Dynamic Graphs

Xiafei Qiu, Wubin Cen, Zhengping Qian, You Peng, Ying Zhang, Xuemin Lin, and Jingren Zhou. 2018. Real-time constrained cycle detection in large dynamic graphs. Proc. VLDB Endow. 11, 12 (August 2018), 1876–1888. https://doi.org/10.14778/3229863.3229874

ABSTRACT

随着图数据在越来越多的互联网应用程序中普遍存在，持续监控动态图中的结构模式，以生成实时警报和触发提示操作，对许多应用程序来说变得至关重要。本文提出了一种新的系统图，可以有效地检测动态图中的约束循环，并实时返回令人满意的循环。为每个查询构建并有效地维护了一个基于热点的索引，从而大大加快了查询时间，实现了较高的系统吞吐量。GraphS系统是阿里巴巴开发的，基于周期检测主动监控各种在线欺诈活动。对于一个具有数亿条边和顶点的动态图，系统能够处理每秒数万条边更新的峰值速率，并找到所有具有预定义约束的周期，延迟99.9%为20毫秒。

1. INTRODUCTION

随着信息技术的快速发展，由越来越多的应用程序生成的数据正在被建模为图形。一方面，图结构能够编码实体之间的复杂关系。例如，包括社交网络、电子商务交易和电子支付等。这是这样的图的典型特征将包含数亿条边和顶点。对这种大规模图上的复杂分析为底层数据集和不同实体之间的交互提供了有价值的见解。另一方面，这些图的结构变化在本质上是恒定的，这使得它们非常动态，以及由实体产生的连续的信息流。设计一个高效的图形系统来大规模存储和管理动态图形，并提供实时分析来探索和挖掘快速演化的结构模式是非常必要且具有挑战性的。
本文研究了大动态图中的一个连续约束循环检测问题。特别是，对于动态图的每一条传入的边，其目标是识别新生成的周期，并分别将它们返回给一组连续的查询。每个查询都可以要求满足一些预定义约束的周期，如长度和属性约束。实时检测受约束的周期对许多实际应用程序都是有价值的。我们在电子商务和个人金融的背景下使用了两个简化的现实世界的例子来说明这类操作的重要性。

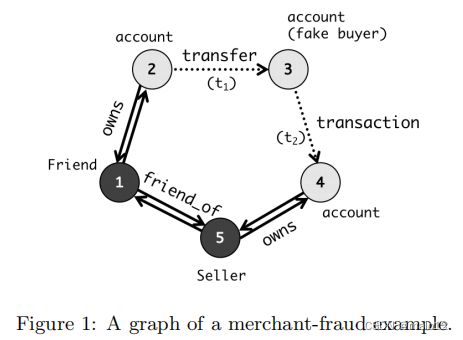
图1为电子商务平台中买卖双方之间的简化图。我们将个人用户（买家或卖家）和他们的账户表示为图中的顶点。边有两种类型。一种类型的静态边（实线）建模帐户的关联用户和不同用户之间的关系，而包括支付活动在内的在线交易被表示为相应顶点的动态边（虚线）。为了增加一种商品的受欢迎程度，以提高未来的销售，虚假交易被人为地增加过去的交易的数量。在本例中，这是通过第三方账户（顶点3）实现的，从那里放置一个正常的订单，并在时间t2将其支付（边缘3→4）完成。但是，卖方（顶点5），假买方（顶点3）支付的款项之前在时间t1时通过卖方的朋友（顶点1）使用他/她自己的账户（顶点2）转给顶点。整个过程涉及到多个实体，过程都相当复杂。有趣的是，它在图中生成了一个循环（1→2→3→4→5→1），这可以作为可能存在欺诈的有力迹象。

图2表示了一系列使用图表的信用卡交易，并描述了一个有趣的信用卡欺诈案例。通过使用假身份证，一个“罪犯”（顶点2）可以从一个银行（顶点4）获得短期信贷。在一个商人（顶点3）的帮助下，他试图在t1时刻通过伪造购买（边2→3）来非法套现。一旦商人从银行（顶点4）收到付款（边4→3），他就试图分别在时间t3和t4通过一个中间人（顶点1）将钱（边3→1和1→2）寄回给“罪犯”。如果系统能够实时检测循环（2→3→1→2），就可以及时阻止此种欺诈。
在这两个例子中，这种欺诈活动成为了这个电子商务平台的主要问题之一，比如阿里巴巴的淘宝和购物商城，这些图表可能包含数亿个顶点（用户）和数十亿条边（支付、交易）。在现实中，整个欺诈过程可能涉及一个复杂的交易链，通过许多实体，这需要复杂的周期检测，并有各种约束，如周期的长度和要识别和监控的交易的数量（边缘）。此外，该图正在以每秒数万个事务的巨大速度进行更新。如何在如此大的动态图中快速检测各种受约束的周期，是及时防止欺诈和防止潜在的财务损失的关键。
之前提出的图形处理框架，如Pregel [17]和GraphX [11]，通过利用图形划分和数据并行性来实现离线分析，以实现高吞吐量和良好的可伸缩性。然而，我们面临的是一项要求显著降低延迟的任务。这个数量上的差异大到足以需要对架构进行质量上的改变。流媒体系统一直是研究的热点。推特Storm [4]和Apache Flink [3]最近一直专注于大规模流媒体的高级编程抽象和弹性。虽然容错很重要，但我们需要对流数据执行复杂的图遍历，据我们所知，这超出了当今流行的流处理器的表达能力。它很可能还需要进一步的专业化来满足延迟目标。
在静态图中寻找最短路径的索引已经得到了广泛的研究。然而，它并不直接适用于我们的情况，它需要在高度动态的图中连续地定位所有可能的循环。此外，这种索引的空间和维护开销通常太高，无法对动态图进行扩展。或者，一种简单的方法使用宽度或深度优先搜索来遍历图。这种方法给重复计算带来了巨大的开销。此外，真实世界图的偏态往往会导致极其不平衡的响应时间。如后面所述，当查询遇到一些具有高度连接性的顶点时，该方法可能会引入指数级增加的可能路径来探索，并在响应中导致重大延迟。
在本文中，我们提出了一个新的系统，称为图，以应对上述在快速变化的图上的连续约束周期检测的挑战。它利用动态索引结构来优化内存使用和查询效率之间的权衡，并降低维护成本。具体来说，对于每个查询，我们提出了基于热点的索引，它可以有选择地应用于图的某个部分，并利用各种启发式（例如，内存使用和顶点连接）来平衡成本和效率。随着图的发展，系统会自动适应自己，以捕获新的热点，并相应地更新索引。为了在没有优化查询性能的情况下处理较高的边缘更新率，该索引作为搜索评估的副产品被有效地维护。额外的优化技术被设计为同时和乐观地评估受约束的周期，以增加系统的吞吐量，同时保证正确性。GraphS是阿里巴巴部署的一个真正的生产系统。它作为几个关键业务的基础，实时检测受限的周期，并在非常动态的环境中防止欺诈。该系统可以处理一个具有数亿条边和顶点的动态图，并且能够处理每秒数万条边更新的峰值速率，并在几毫秒内找到所有具有预定义约束的周期。
论文的其余部分组织如下。我们正式地定义了这个问题，描述了直接的解决方案，并在第2节中演示了这些挑战。然后，我们在第3节中提出了一种新的基于热点的指标。在第4节中，我们系统地描述了图形系统及其内部结构。我们在第5节中进行了实验，并演示了性能的改进。最后，我们在第6节中调查了相关的工作，并在第7节中进行了总结。

2. PRELIMINARY

在本节中，我们首先正式介绍了动态图中的约束循环检测问题，然后给出了一个基于深度优先搜索的基线解决方案。

2.1 Problem Definition

设G =（V，E、AV、AE）表示一个有向图，其中(1) V是一组顶点；(2) E⊆V×V，其中e（u，v）∈E表示从顶点u到v的一条边；(3) AV（AE）表示顶点（边）的属性集合。例如，我们使用t (e)来表示e边的时间戳（t∈AE）。在这个系统中，我们有两种类型的边：静态边和动态边。对于每一个静态边e（例如，两个用户之间的朋友关系），我们设置t (e) =∞，其中的边永远不会过期。对于动态边（例如，用户之间的转账），我们假设它们有逻辑/应用程序时间戳，表示事务时间，并且它们按顺序到达。在本文中，我们使用流行的滑动窗口模型来捕获图g的动态。特别是，我们维护一个系统时钟c来表示当前时间，它在每条边到达时更新。在图G中，具有t (e) + W≤c的动态边e将过期，其中W为滑动窗口的长度。当上下文清晰时，我们使用G来表示滑动窗口模型下的动态图。在系统中，动态图G由一个具有所有顶点和静态边的基图G0初始化。然后在动态边缘到达和到期时不断更新。
我们将使用以下动态图g的符号。从顶点v到v0的路径p是一个顶点序列v=v0，v1，v1…，vn=v0，这样（vi−1，vi）∈E为每个i∈[1，n]。我们也可以使用p（u，v）来表示从顶点u到v的路径。路径（循环长度）p，用len §表示，是路径（循环）中的边数。如果没有顶点和边的重复，我们说一个路径是简单的路径。一个循环是一个具有v0 = vn和len §≥3的路径p。如果没有对顶点和边的重复，而不是对起始顶点和结束顶点的重复，那么一个循环就是一个简单的循环。
定义1（长度约束）。如果p是一个预定义数，则len §≤k，则说路径或循环p满足长度约束。
在实际的应用程序中，用户还可以根据不同业务逻辑的边和顶点的属性值施加其他约束。本文将单个边和顶点上的简单谓词考虑如下。
定义2（属性约束）。让fA（）表示一个用户定义的布尔值函数对边或顶点的属性值，我们说一个边e (resp。如果是fA (e)，则满足属性约束。fA (u))是真的。如果每条边和节点都满足属性约束，则一个路径或循环满足属性约束。
定义3（连续周期查询）。连续循环查询q =（k、fA（.））将增量地报告动态图G上每条新边的到达所产生的新的简单循环，其中每个循环同时满足长度和属性约束。
问题声明。给定动态图G和一组连续的（受约束的）周期查询Q，对于每条传入的边e，我们的目标是开发一个系统来实时支持每个查询Q∈Q。
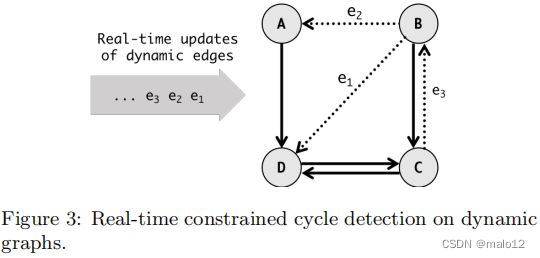
例子1。图3展示了一个连续约束周期检测的例子，其中三个动态边{e1，e2，e3}按顺序到达。假设q的长度约束为3，且没有属性约束。结果表明，在e3(C、B）到达时，将报告该循环（B、D、C）。请注意，该循环（B、A、D、C）不满足长度约束，因此将不会被报告。

2.2 A Baseline Solution

给定动态图G和查询q的属性约束，我们可以通过过滤不满意的边和顶点，很容易地得到一个图Gq。显然，我们不需要为每个单独的查询q实现Gq，因为通过在搜索过程中丢弃不满意的顶点和边，属性约束可以很容易地集成到循环检测算法中。因此，下面我们将关注长度约束的周期检测。
对于每个简单路径e（d，≤），一个简单路径e（d，d）将产生一个长度约束k + 1的简单循环。所以关键是找到长度约束下的所有简单路径{p（s，d）。下面的算法使用深度优先搜索（DFS）来枚举从源顶点s到目标顶点d的所有简单路径。在每次更新（=，=）时，算法以有向图G的当前快照、源的顶点=和目标顶点G的=，以及参数=.=作为长度约束作为输入。它输出G中从s到d的所有简单路径，长度为k。搜索从源顶点开始，沿着有向边开始。一旦它到达目的地，一个叶顶点或当前的长度已经是k，它就会返回以继续搜索其他可能的路径。

分析。在图4中，我们报告了具有长度约束的连续约束周期查询的响应时间k = 6反对新边缘的到来（详细的数据描述见第5节）。

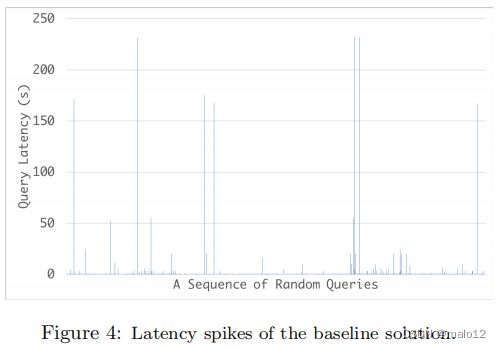
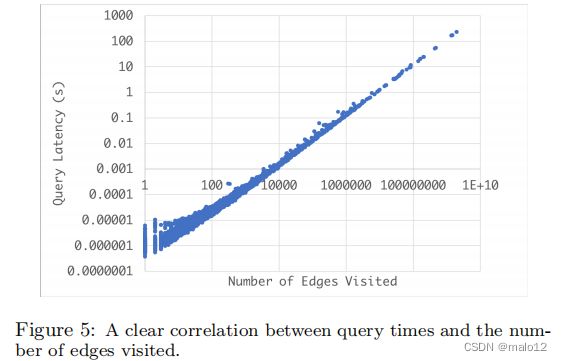
结果表明，有许多峰值，其中进入的边缘消耗的时间明显比平均时间更长。这些峰值将严重恶化系统的吞吐量，因此在实时系统中是不可接受的。造成这种现象的关键原因是存在一些热点，即输出度非常高的点。每当遇到一个热点时，算法1中所访问的边数就会大大增加。图5显示了查询访问的边数与响应时间之间的明显相关性。这促使我们开发一种基于热点的索引技术来缓解这一问题。

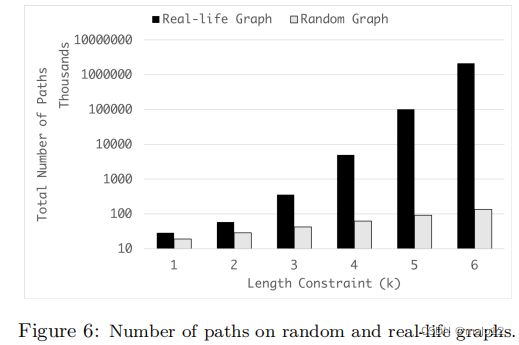
进一步解释为什么热点的存在伤害了系统性能，图6报告的路径长度k在我们的真实图评估实验以及随机图与相同数量的顶点（518，959，261）和边缘（2，088，968，416），遍历从10000随机选择的顶点。结果表明，由于热点的存在，k长度路径的数量（即访问的边）增长非常快。特别是当=3和=5时，约93%和99%的路径分别遇到至少一个热点（导出度不小于40）。请注意，从直观上看，由于边的总数相同，随机图中的路径总数应该大于真实图中的路径总数。然而，当长度约束k不大时，现实网络中路径的数量增长得更快。请注意，在我们的应用程序中使用的k值并不大。

3. HOT POINT BASED INDEX (HP-Index)

如第2.2节所述，连续约束周期检测的关键技术是长度约束周期检测，关键挑战是如何处理搜索过程中遇到的热点。在本节中，我们提出了一种新的基于热点的索引技术，即HP-Index，以支持长度约束周期检测。特别是，第3.1节介绍了HP-Index的动机。第3.2节和第3.3节给出了索引结构和相应的搜索算法。第3.4节显示了高压指数的动态维护。第3.5节讨论了如何处理多个连续的受约束的周期查询。

3.1 Motivation

如在第2.2节中所讨论的，在现实生活图中，热点（即具有大量输出边的顶点）的存在可能会严重恶化系统的吞吐量。如图7所示，当边（u4，u1）出现时，我们可以通过从u1开始进行DFS搜索，枚举长度约束为k = 7的路径{p（u1，u4）}。这种方法的一个缺陷是，当遇到一个有许多输出边的顶点时，搜索空间可能会迅速爆炸。例如，当访问图7中的顶点h1时，它可能会出现大量的路径，其中许多路径在7跳内无法到达u4。

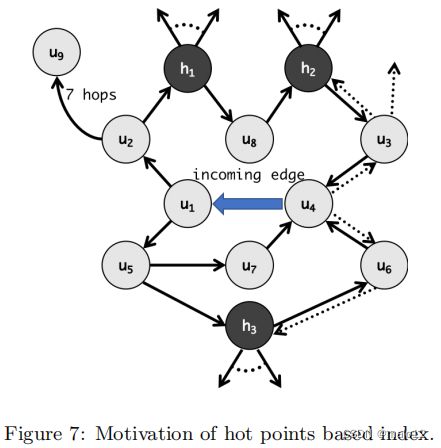
这促使我们建立基于热点的索引，这样我们就可以避免在遍历图时显式地探索热点的输出边。基于热点的索引技术的关键思想是持续保持每对热点的长度约束路径。通过这样做，我们可以在图g上对u1进行DFS。当遇到一个热点（如图7中的h1和h3）或违反长度约束时，一个搜索分支将被挂起。我们还在G的反向图上对u4进行DFS（即所有边都颠倒，图7中用虚线表示），并在遇到热点或违反长度约束时挂起搜索分支。然后利用热点间预先计算的长度约束路径，生成具有长度约束的路径，可以显著减少搜索空间。
特别地，为了满足大型动态图的实时响应时间要求，我们提出的索引技术应该具有以下特性： (1)索引大小较小；(2)可以快速更新；(3)可以有效地枚举任意两个顶点的所有长度受约束的简单路径。
通过分析在我们的案例研究中使用的图（有518,959,261个顶点和2,088,968,416条边）的结构特征（详细的数据描述见第5节），我们发现它是一个高度倾斜的无标度图。例如，只有5274个度大于4000的顶点。此外，这些长度小于6的顶点之间的路径数只有1,399,383条，远小于图的大小。这表明，我们能够维持相当数量的热点和它们之间的长度约束路径。
在此基础上，我们开发了针对每个输入边的有效的循环检测算法（即路径枚举算法）。同时，我们还证明了指数维护是搜索过程的副产品。通过这样做，我们将显示索引技术满足所需的三个属性。正如我们的案例研究所示，我们提出的HP-Index不仅显著减少了响应时间中的峰值数量，而且还提高了平均处理时间。

3.2 Index Structure

我们将在本小节中介绍HP-Index结构。热点。设d (v)是一个顶点v的度，t是阈值。设H是G中满足∀h∈H，d (v)≥t的顶点集合，称为热点。注意，我们在搜索处理中也使用顶点的反向边，因此我们同时考虑顶点的内外度。
对于每一对热点hi，hj∈H，索引包含hi和hj之间的所有（预计算）路径，这些路径的长度小于或等于k，并且每条路径不经过任何其他热点。这些路径被组织成一个索引图，用Gidx表示。索引图只包含热点h∈∈。每条边代表一条路径，由其长度加权。
此外，我们还维护了一个反向图g0来支持查询处理。它有与∈相同的顶点集。对于边，e 0 h v，ui∈g0当且仅当eh u，vi∈∈。注意，我们不会立即加倍存储空间，因为静态边通常是双向的。此外，我们也不需要复制这些边的属性值。

3.3 Search Algorithm

对于每一个进入的边h u，vi，我们在G中搜索从s = v到d = u的长度小于或等于=的所有简单路径(abbr。，采用如图8所示的以下三个步骤。

步骤1。从源顶点开始进行DFS搜索。当到达：i) d时（例如，图7中的路径u1u5u7u4）时，搜索分支就会停止。ii)已经有长度k（例如，路径u1u2…图7中的u9）。iii)遇到一个热点（例如，图7中的路径u1u2h1和u1u5h3）。
请注意，这与简单的方法相同，只是我们在遇到热点时挂起搜索分支。如果在搜索过程中没有出现任何热点，那么我们就已经立即根据需要确定了所有的k个路径。否则，我们需要考虑涉及热点的路径。
用L，我们表示在步骤1中遇到的热点的集合。对于每个热点（顶点）h∈L，我们记录从源到h的所有路径，用p (h)表示。然后我们进入第二步。
步骤2。从反向图G0中的目标顶点d进行另一次DFS遍历，如果达到：(i) s时停止。（ii）已经达到长度k. 2（iii）满足一个热点（例如，图7中的h2和h3），它将保持在集合R中。
对于每个热点（顶点）h∈R，让p 0 (h)在步骤2中记录所有以反向边结束于h的路径。让S = R∩L，我们可以通过检查p (h)和p 0 (h)中所有可能的有效路径组合来识别只有一个热点∈的新的∈路径。例如，我们可以通过考虑p（h3）中的路径u1u5h3和p 0（h3）中的路径u4u6h3来立即识别路径u1u5h3u6u4。
步骤3。此步骤将通过使用索引结构来识别涉及多个热点的剩余路径。对于每个热点嗨∈L，我们进行深度优先搜索长度约束k索引图Gidx识别热点{hj}⊆∈.对于每一对热点嗨和∈，k路径从嗨到∈，表示，j可以识别在上面的搜索。然后，通过连接来自p（hi）、Pi、j和p 0（hj）的部分路径，可以推导出从s到d的k个路径。注意，我们需要从p 0（hj）反转路径。例如，我们在图7中有u1u2h1∈p（h1）、h1u8h2∈P1,2和u4u3h2∈p 0（h2）。然后我们就可以得到一个有效的路径。
备注1。注意，我们假设s和d都不是上述算法描述中的热点。我们可以简单地设置L = {s}。R = {d})。d)是步骤1中的一个热点。 2).

3.4 Index Maintenance

在本小节中，我们将展示如何在边到达和到期时持续保持hp指数。
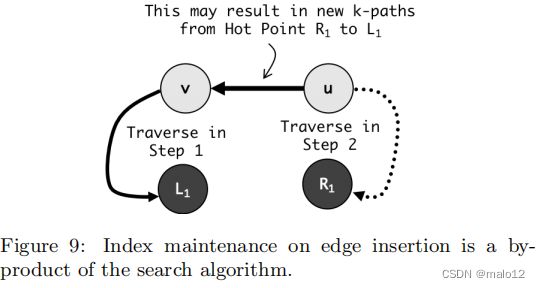
边缘插入。当一条动态边h u，vi到达并插入到动态图G中时，我们需要在插入e所产生的热点之间添加新的k-路径。假设u和v都不是热点3。如图9所示，设p是从热点r1到l1的一个新的k路径。显然，p必须包含进入的边h u，vi。由于len §≤k，它从v到L1的子路径和从u到R1的反向子路径必须分别在步骤1和步骤2中检索。因此，我们可以通过检查在步骤1和步骤2中获得的L1和R1中的路径来立即识别p。例如，在图7中，我们有一个新的路径huuu4u1uuh1u11。在步骤1 w.r.t h1中检索子路径u1u2h1，在步骤2 w.r.t h2中检索子路径u2u3u4的反向路径，即u4u3h2。

边缘删除。假设索引的k个路径由一个基于边id的反向索引来维护，我们可以立即识别出相关的路径，并在一条边到期时删除它们。在我们的实现中，我们采用了一种延迟策略，如果路径的任何一条边过期，路径设置为无效。以后可以批量删除无效的路径。
调整HP指数。随着动态图G的加入，度分布可能会随着变化而变化，因此我们可能需要调整hp指数来适应变化。我们可以很容易地调整阈值t来增加或减少热点的数量。当一个顶点u作为一个新的热点时，我们需要通过对G（从u开始的k路径）和反向图G0（以u结束的k路径）应用DFS（算法1）来枚举到现有热点的k路径，而不探索任何热点。回想一下，一个热点只能是HP-Index中k个路径的开始或结束顶点。因此，我们还需要从hp-索引中移除k-路径x u y。注意，在上述计算中同时检测到xu和uy。当从HP-Index中删除一个热点v时，将删除其所有相关路径。此外，v可以作为一个非热点包含在热点的k路径中（即，而不是HP-Index的k路径中的开始或结束顶点）。设L = {x}表示有的热点hp指数中的k路径xv。同样地，让R = {y}表示具有k个路径vy的热点。我们连接了每一条可能的路径{x v y}，并包括那些满足长度约束到HP-Index的路径。

3.5 Coping with Multiple Continuous Constrained Cycle Queries

在系统中，我们可能需要支持多个具有不同长度或属性约束的连续查询。对于具有相同属性约束的查询，我们只需要处理具有最大长度约束kmax的查询，因为它的输出包括了对其他查询的所有有效周期。对于查询q的属性约束，我们只需要保留有效的顶点和边，这可能会导致一个更小的动态图Gq和相应的HP-Index。为了方便系统的并发性并支持不同的属性约束，我们为每个单独的查询维护一个HP-Index。更多的细节将在下一节中讨论。
备注2。与长度约束类似，我们可以考虑对具有相似属性约束的查询的计算共享。这将是一个有趣的未来研究方向，并超出了本文的范围。

4. SYSTEM IMPLEMENTATIONS

在本节中，我们首先介绍图形的整体体系结构。然后描述了能够有效地存储和更新图数据、持续监控图结构、及时返回受约束周期的系统内部组件。最后，我们讨论了额外的系统优化，以提高系统吞吐量和提供容错能力。

4.1 Architectural Overview

4.1图10显示了图形系统的架构概述。图形存储区负责持久地存储图形数据。对于低延迟访问，系统还使用如下所述的优化紧凑表示，在主存中维护图形数据的副本。
用户可以为受约束的周期定义一个查询，并将其作为一个连续的查询注册到系统（如步骤(1)所示）。对于在t时刻注册的每个查询，图将返回所有查询涉及至少一个时间戳大于t的动态边的循环。系统增量检测周期如下。随着边缘更新不断出现（如步骤(2)所示），系统首先将它们应用于图形存储（如步骤(3)所示），然后通知每个查询的更新（如步骤(4)所示）。每个查询都计算满足周期的新实例，如果需要，计算额外的约束，并将结果返回给用户（如步骤(5)所示）。用户可以在任何时候停止或中止一个连续的查询。
在本节的其余部分中，我们将详细介绍每个组件，并详细描述其实现。

4.2 Graph Store

如第2节所述，图中有两种类型的边。系统将分别存储它们，以优化性能。
1.静态边缘。它们不会在查询生命周期中发生更改，并且只是偶尔以批处理的方式进行更新。
2.动态的边缘。它们每个都有一个时间戳，并在定义的时间间隔后过期。
图11显示了一个示例图。带实线的边是静态边，带虚线的边是动态边。从概念上讲，图存储维护了以下两个映射。

图拓扑结构。这是一个从一个顶点到其边缘的映射。
属性。这是一个从顶点或边到其属性的映射。
由于一个图可能包含数亿条边和顶点，因此最大化内存效率和实现快速查询性能是很重要的。

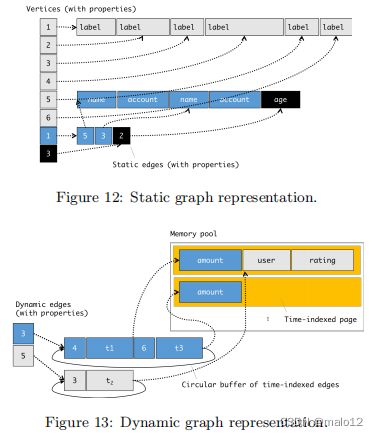
紧凑的表示。图12和图13分别显示了示例图的静态图和动态子图的内部表示。对于静态图，边的列表被连续地存储在一个数组中，并且它们的起始偏移量被存储在映射中。此外，我们根据它们的目标顶点对边缘进行排序，以便能够实现更多的顺序内存访问。
我们使用了一种针对只有一条边的顶点的专门编码，这在我们的数据集中有很大的比例（近67%），通过将边缘信息直接存储在地图中，而不需要索引到一个单独的内存位置。这就节省了约17%的内存。
边列表中的每个条目都包含其目标顶点、时间戳（用于动态边）和指向其属性值的指针。对于属性值，我们为每个顶点或边引入了“模式”，它定义了关于它们的属性名和值类型的元数据信息。然后，针对不同的类型使用特定于模式的编码。
我们将固定长度的属性值组合在一起，并保持在连续内存中没有任何间隙。在这种情况下，它们的偏移量只需要按每个模式进行计算。对于可变长度的值，大小信息必须与该值一起存储。
如图13所示，我们使用一个循环缓冲区来维护动态边缘的列表，按照它们到达（和过期）时间的顺序。在每个边插入上，圆形缓冲区会立即为那个特定的顶点进行更新。该顶点的超时边被标记为从列表中删除，尽管我们推迟了其属性值以及其他顶点的其他超时边的实际删除，如下所述。
延迟边缘删除。当系统负载较低时，使用在后台运行的垃圾收集机制，会延迟删除边缘属性以及来自其他顶点的边。由于每条边都有一个时间戳，因此过时的边不会影响查询的正确性。
对可变长度属性的高效内存管理具有挑战性。频繁分配和释放的成本不再可以忽略不计，并可能导致内存碎片化。因此，如图13所示，系统使用一个固定长度页面的内存池来存储动态边的属性。每个页面都标记了它所包含的属性的最新过期时间和是由一个垃圾收集进程进行管理的。如果过期时间过去了，系统可以完全释放页面，而不是一个接一个地释放属性。

4.3 Query Evaluation

如前所述，该系统支持多个并行的并行查询。每个查询都分配了一个专用的进程，系统提供了独立于其他查询的容错能力。图14使用Q1为例来说明连续的查询评估。

提交连续查询时，将根据当前快照构建热点索引（见步骤(1))。与原始图及其性质相比，这种指数相对较小。我们使用简单的哈希映射，并将路径按其长度排序。随着新的边缘更新（如步骤(2)所示），系统使用热点指标评估是否出现新的令人满意的周期并立即输出（如步骤(3)所示）。最后，它还将热点指数作为过程的最后一步（如步骤(4)所示）。
随着边缘更新的顺序出现，系统可以从概念上逐个消耗每个边缘更新。然而，这个过程是串行完成的，可能无法应对传入的边缘更新的峰值。为了提高总体吞吐量，系统维护一个线程池，以乐观地处理不同的边缘更新，而不等待以前的边缘更新完成。可以根据需要动态地调整线程池的大小。
在大多数情况下，当两个边的更新涉及到图的不同部分和热点时，它们可以独立地和并发地处理，而不影响结果的正确性。
有时，后续的边缘更新可能依赖于早期边缘更新中的索引维护。如果发生这种情况，将发出一个补偿查询，以评估可能丢失的周期。例如，对于给定的边缘更新序列…，e1，e2，…，，在e1更新热点索引之前，系统分配一个线程，使用当前版本的热点索引来评估e2，并不等待返回结果。该系统还记录了哪些热点是在评估e2时涉及到的。当e1最终完成时，系统检查修改后的热点指数是否与e2所依赖的热点集相交。如果是，则执行如下新的补偿查询：重新计算e2，只返回包含时间戳为e1的边的满足周期。
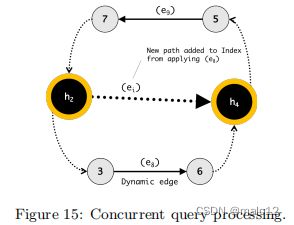
图15显示了一个应用两个并发边更新的示例。我们假设……，e8，e9，…作为添加的新边的序列。在将e8应用于热点索引之前，系统会发布新的线程以应用更新e9。它在e8更新之前使用一个旧版本的热点指数，并迅速返回令人满意的周期。在这种情况下，更新e9依赖于热点h2和h4之间的路径。如果应用e8没有在这两点之间添加任何新的路径，则不存在潜在的冲突，并且可以同时执行这两个更新，而不会丢失任何结果。如果应用e8确实添加了一个新的路径，例如本例中的ei，那么应用e9可能会错过一些潜在的循环。一旦e8更新了热点索引，就会对e9发出一个补偿查询，以计算具有一个时间戳大于所操作的热点索引的时间戳的边的周期。

4.4 Fault Tolerance

GraphS系统通过运行多个系统实例之间复制的图形来实现高可用性。在被所有实例使用之前，使用可靠的存储持久化。这确保了事件的确定性顺序，以便在发生故障的情况下产生一致的结果。
在每个实例中，我们将不同的连续查询和它们的hp索引分离到不同的进程中。可以通过共享内存访问该图。如果一个连续查询失败，我们对剩余的健康实例进行快照，记录相应输入的序列号，并使用该信息恢复计算，可能在另一个服务器上。
为了检测故障，GraphS监视CPU、内存和网络资源利用率，以及查询响应时间，以及许多其他指标。这些信息还用于调整性能关键型配置，例如垃圾收集的频率，以最大限度地减少对查询延迟的影响，同时确保有足够的可用内存。

4.5 Additional Optimizations

哈希映射在GraphS的整个实现过程中被广泛使用，以有效地存储和查询顶点属性、边缘信息和索引路径。在我们的库中的默认散列映射实现使用线性探测来解决冲突，即在数组中找到下一个可用的插槽。这样的实现非常高效，如图16所示。但是，当我们试图将一个非常大的图拟合到有限的内存中时，冲突率会显著增加，从而导致较差的延迟。解决散列冲突的另一种常见方法是将发生冲突的条目链接到链表中。由于我们的顶点集保持稳定（尽管边来来去去），链表的开销可能很大，如图所示，因为有额外的指针需要维护，而且连续访问不太可能适合CPU缓存行。
我们在哈希映射的实现中结合了这两种策略。我们首先尝试使用线性探测来解决任何冲突。如果冲突在m（可配置参数）探测之后仍然存在，我们切换为使用冲突的链表。这种设计提高了内存效率和访问延迟（因为它对CPU缓存线比链接更友好），如图16所示。

5. EVALUATION

该图表是使用阿里巴巴的Rust [24]开发的。该系统被部署在生产环境中，以主动监控不同业务场景中的动态图的受约束周期。检测到的循环实时流到控制中心，根据其他数据分析和估计的严重程度将其分为几组。然后相应采取进一步的行动，包括对有问题的交易进行审查、自动取消欺诈交易、将可疑人员列入黑名单等。对各种业务逻辑和策略的详细描述超出了本文的研究范围。然而，这种受限的循环检测在整个过程中发挥了关键作用。
下面的报告使用从实际工作负载中选择并在生产集群上进行评估的受约束的周期查询。所有的查询都是在Intel ® Xeon ® E5- 2650服务器上执行的，该服务器具有32核（2.60 GHz）和128GB内存。在第5.1节中，我们给出了动态图，并概述了其特征。我们将在第5.2节中描述所选择的查询及其属性。在第5.3节中，我们系统地评估了此类查询在生产过程中的性能，包括hp-索引的选择及其对查询性能的影响。最后，我们演示了其可伸缩性，并在第5.5节中讨论了高频更新对系统性能的影响。

5.1 Dynamic Graph

动态图形数据集是基于阿里巴巴电子商务平台上的活动，包括不同类型的实体、其中的实时交易和支付。图形数据同时包含静态信息和动态信息。例如，这些顶点代表单个用户和帐户。静态边表示用户（如朋友）之间的关系，以及从帐户到其所有者的映射。实时交易和支付是由动态边缘建模。
对于给定的一天，这个特定的图正在以每秒3000条边的平均速率进行更新。在峰值时，每秒会增加超过20,000条新边。从一个随机的快照中，我们观察到518,959,261个顶点和2,088,968,416条边。它们消耗了大约73GB的内存，包括顶点和边缘属性。
图17显示了顶点度的完整分布（包括内边和外边）。80%的顶点的度小于10，而最大的顶点度超过78,000。

5.2 Cycle Detection Queries

对动态图连续地执行具有不同约束条件的各种查询。具体来说，我们从生产中选择了一个具有代表性的连续查询，并研究了其性能。它检测上图中的6跳周期，超过48小时的滑动窗口。在边缘上有一个附加的约束来过滤掉某些类型的事务。
该查询用于监视涉及特定类型的用户活动的虚假事务。一个满足约束的子图有12,243,538个顶点和33,826,783条边。通过利用该约束条件，系统从这个较小的图中构建HP-Index。但是对于查询处理，过滤仍然是通过在运行时遍历原始图来执行的。
为了在不同的条件下重复实验，我们从实际生产中收集了50万次更新，并将其用于其余的评估。

5.3 Performance Evaluation

我们将在本小节中评估hp指数的性能。图18和图19分别显示了热点路径和索引路径的数量（具有内存大小），其中度阈值t从10到5120变化。正如预期的一样，随着阈值t的增加，热点的数量减少。与预期的一样，随着阈值t的增加，热点的数量和指数的大小也会减小。此外，与我们的设置下的图大小相比，索引大小非常小。

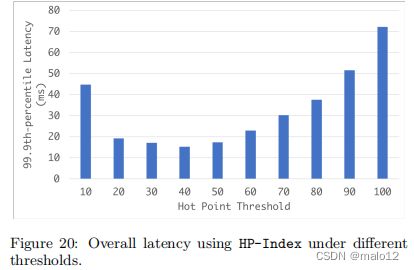
图20显示了在从10到100变化的不同阈值t下使用HP-Index的查询响应时间。我们报告了99.9%的时间，这是在线系统性能评估的常用指标。在每个设置下，我们将在图20中报告总体延迟，以及更详细的查询响应时间（步骤1、2和3）和图21中的索引维护时间。毫不奇怪，维护成本接近于零，从这个数字中很难看出。然而，令人惊讶的是，索引查找时间相当重要，甚至主导了总查询时间，特别是当搜索遇到更多的热点时（因为它必须检查它们的所有组合）。


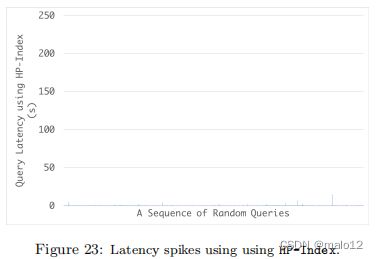
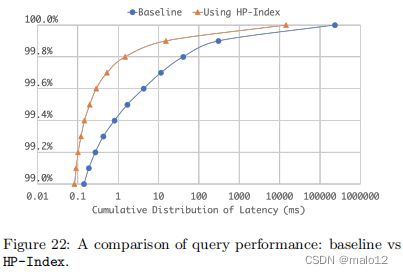
尽管如此，有了查找成本，我们的算法也可以比没有索引的直接方法（在算法1中）获得相当好的整体性能。图22通过显示基线算法的响应时间的累积分布和使用指数的最佳数量（在t = 40），详细说明了性能比较。为了由延迟定义为99.9%（及以上）的坏情况，HP-Index实现了一个数量级的改进。
在图23中，我们显示了在图4中使用的相同的更新/查询跟踪的响应时间。结果表明，我们的算法显著地缓解了延迟峰值。

5.4 Scalability

如第4节所述，我们利用一个线程池来乐观地同时应用边缘更新。这种设计提高了系统的吞吐量，并展示了良好的可扩展性。在图24中，我们报告了随着核数量的增长，图的吞吐量。结果表明，图几乎使用多核线性扩展来并发处理传入的更新。

5.5 Coping with Graph Changes

虽然我们将在第3.4节中讨论如何调整HP-Index的技术，但在我们的应用程序中，网络的度分布在边缘的进入和过期时不会发生太大变化。图25通过报告24小时内热点数量（包括在t=40时的增减）的每小时变化的百分比来证实这一点。

6. RELATED WORK

以前的大量工作都集中在循环枚举、模式匹配和最短路径等方面。在本节中，我们将简要回顾一下密切相关的工作。

6.1 Path and Cycle Enumeration

关于在图[20,15,18]上列举所有简单的路径或循环，已经有很长的研究历史了。另一个研究方向（例如，[19]）是计算或估计两个给定顶点之间的路径数量，这是一个众所周知的#P难题。但由于涉及到矩阵运算或近似解的采样技术，这些技术不能简单地推广到大规模动态图来解决我们的问题。在文献中已经对增量循环检测的问题进行了研究（如[16,22,5]）。然而，由于一些严格的假设，如无环图[22]和低维图[16]，所提出的技术不能简单地扩展到检测大规模现实网络中具有长度约束的周期。

6.2 Pattern Match

模式匹配已经在各种计算环境中得到了广泛的研究（见[10]的调查）。一些研究工作已经致力于连续精确模式匹配的问题，其目的是在图的更新时逐步识别所期望的子图模式。在[9]中，提出了IncIsoMat在图更新时连续识别子图匹配，其中计算一个候选子图区域以减少研究空间。图流[14]应用最坏情况最优连接算法来增量评估每次更新的子图匹配。SJ-Tree [8]为查询图构造左深树，并在树节点中持续保持部分匹配。
通过将长度不大于k的循环作为一组模式，我们可以应用连续模式检测算法来识别长度约束循环（LCCs）。然而，由于具有2≤§≤k−1的每个路径p都可能是部分解，因此使用基于部分解的技术作为SJ-Tree [8]是不可行的。

6.3 Reachability and Shortest Path

给定图中的两个顶点u和v，点拓扑可达性和最短路径查询是图中最重要的两种查询类型（参见[27]和[23]）。现有的用于可达性查询的主存算法可分为两类：仅限标签搜索和在线搜索。仅使用标签的方法专注于压缩图的传递性，以获得更小的索引大小，以用于快速查询处理。最近的研究包括TF-Label [6]和DL [13]。在线搜索方法通过在运行时借助一组修剪策略从源顶点执行DFS来回答可达性查询。具有代表性的作品包括GRAIL [26]、法拉利[21]和IP+ [25]。最近，在[28]中提出了一种新的DAG约简方法，以进一步加快可达性计算速度。在最短路径计算方面，现有的主存算法也可分为仅标签搜索技术和在线搜索技术。在无标度网络中，最有效的距离查询方法是基于2跳索引。修剪地标标记[1]和希望加倍标记[12]是两种最先进的算法。近年来，可达性和最短路径的计算分别在[29]和[2]中研究了动态图。
上述所有的作品都没有考虑到长度的约束。据我们所知，[7]是唯一现有的研究k长度约束的可达性问题的工作，其中选择图的顶点覆盖中的一组顶点作为集线器，并预先计算每一对集线器的可达性。请注意，针对可达性和最短路径的索引技术可以用于计算长度约束周期（LCCs）时的剪枝目的。如果v不能在（k-1）跳中不能到达u，或者从v到u的最短路径大于k-1，那么进入边（u，v）不能贡献k路径。除了这个事实之外，即如果剪枝失败，我们仍然需要继续计算之外，昂贵的索引维护成本使得这些解决方案在大型动态图环境中不可行。

7. CONCLUSION

在本文中，我们提出了一个由阿里巴巴开发的图分析系统图，以有效地检测动态图中的约束循环。该系统支持具有数亿条边和顶点的大型图，并允许特别的连续查询实时在快速变化的图中识别受约束的周期。对于每个查询，构建一个基于热点的索引并有效地维护，以大大加快周期评估。此外，该系统利用优化的数据布局和高效的内存管理来提高性能，并使用乐观的查询评估来提高系统的吞吐量。GraphS系统部署在阿里巴巴的生产中，基于多个业务的周期检测积极监控欺诈活动。对于一个具有数亿条边和顶点以及每秒数万条边更新的峰值速率的大型动态图，系统能够在一毫秒内找到新形成的周期。
虽然我们在本文中关注循环检测，但图系统能够支持查询具有复杂约束的各种结构模式，例如，树状图模式等。每个查询都需要特定于模式的索引，以在图形更改时加快模式评估的速度。未来的另一项工作是在不同的查询之间共享索引，以在不牺牲单个查询性能的情况下最小化索引维护成本。