Verilog快速入门（8）—— 4bit超前进位加法器电路

Verilog快速入门

(1) 四选一多路器
(2)异步复位的串联T触发器
(3)奇偶校验
(4)移位运算与乘法
(5)位拆分与运算
(6)使用子模块实现三输入数的大小比较
(7)4位数值比较器电路
(8)4bit超前进位加法器电路
(9)优先编码器电路①
(10)用优先编码器①实现键盘编码电路
(11)8线-3线优先编码器
(12)使用8线-3线优先编码器实现16线-4线优先编码器
(13)用3-8译码器实现全减器
(14)使用3-8译码器①实现逻辑函数
(15)数据选择器实现逻辑函数
(16)状态机
(17)ROM的简单实现
(18)边沿检测

---

---

一、题目描述

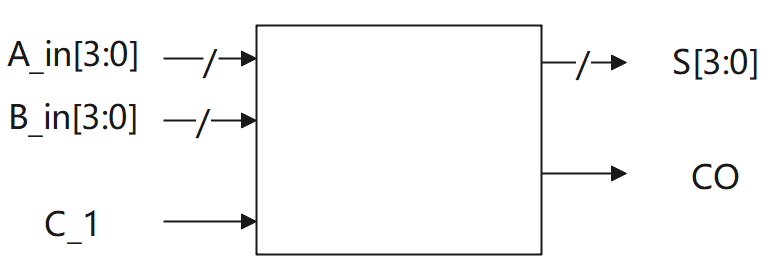
输入描述：
输入信号：
A_in[3:0],
B_in[3:0]
C_1
类型：wire
输出描述：
输出信号：
S[3:0]
CO
类型：wire

二、解析与代码

以下内容摘自Leonico题主解析

1. 半加器

它不考虑进位输入。其中A和B是两个加数，S是和，$C_o$是进位输出。

assign S     = A ^ B;
assign C_out = A & B;

2. 全加器

全加器是多bit加法器的基础。$C_i$是进位输入，$C_o$是向上进位输出。

下图中红色路径是全加器的关键路径。

module full_adder(
    input  A,
    input  B,
    input  C_i,
    output S,
    output C_o
);
    assign S    = A ^ B ^ C_i;
    assign C_o  = A & B | C_i&(a^b);
    // assign C_o  = A & B | A & C_i | B & C_i; // 也可以??? 不确定
endmodule

3. 行波进位加法器

Ripple-carry adder, RCA。将全加器串联起来。 虽然RCA结构简单易于理解，但容易看出，每一位的运算结果$S_i$都要依赖进位$C_{i-1}$才能得出。如下图所示，这会使得RCA的关键路径变得很长，而长关键路径会让电路难以满足时序要求。

module rca #(
    parameter width = 4
)(
    input  [width-1:0] A,
    input  [width-1:0] B,
    output [width-1:0] S,
    
    input  C_i,
    output C_o
);
    wire [width:0] C;
    genvar i;
    generate
      	for (i=0; i<width; i=i+1)begin
            full_adder myadder(
                .A    (A[i]),
                .B    (B[i]),
                .C_i  (C[i]),
                .S    (S[i]),
                .C_o  (C[i+1]),
            );
        end
    endgenerate
  	assign C[0] = C_i;
    assign C_o  = C[width];
endmodule

或者

//行波进位
wire C2,C3,C4;
sub_add sub_add_inst1(
	.Ai(A_in[0]),
	.Bi(B_in[0]),
	.C(C_1),

	.Si(S[0]),
	.Ci(C2)
);
sub_add sub_add_inst2(
	.Ai(A_in[1]),
	.Bi(B_in[1]),
	.C(C2),

	.Si(S[1]),
	.Ci(C3)
);
sub_add sub_add_inst3(
	.Ai(A_in[2]),
	.Bi(B_in[2]),
	.C(C3),

	.Si(S[2]),
	.Ci(C4)
);
sub_add sub_add_inst4(
	.Ai(A_in[3]),
	.Bi(B_in[3]),
	.C(C4),

	.Si(S[3]),
	.Ci(C0)
); 
///
module sub_add(
	input Ai,
	input Bi,
	input C,

	output Si,
	output Ci
);

assign Si = Ai ^ Bi ^ C;
assign Ci = (Ai & Bi) ||( (Ai ^ Bi )& C);

4. 超前进位加法器

Lookahead Carry Adder，LCA。超前进位加法器的思想是并行计算进位$C_i$，以缩短关键路径。$C_i$可以直接由加数得到。

超前进位加法器是通过公式直接导出最终结果与每个输入的关系，是一种用面积换性能的方法。
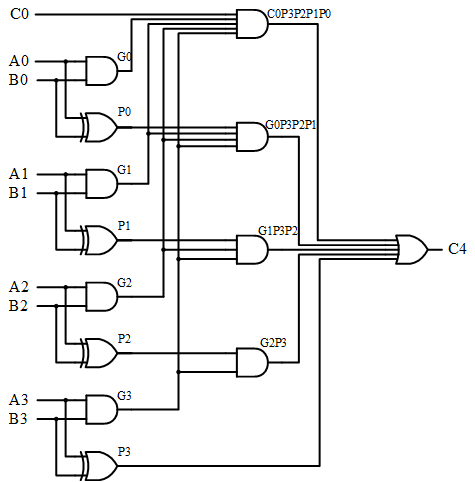
对于4bit LCA，进位输出C4的计算路径如下：

`timescale 1ns/1ns

module lca_4(
	input		[3:0]       A_in  ,
	input	    [3:0]		B_in  ,
    input                   C_1   ,
 
 	output	 wire			CO    ,
	output   wire [3:0]	    S
);
//超前进位

    wire [3:0] C;
     
    assign S[0] = A_in[0] ^ B_in[0] ^ C_1;
    assign S[1] = A_in[1] ^ B_in[1] ^ C[0];
    assign S[2] = A_in[2] ^ B_in[2] ^ C[1];
    assign S[3] = A_in[3] ^ B_in[3] ^ C[2];
    assign C[0] = (A_in[0] & B_in[0]) || ((A_in[0] ^ B_in[0]) & C_1);
    assign C[1] = (A_in[1] & B_in[1]) || ((A_in[1] ^ B_in[1]) & C[0]);
    assign C[2] = (A_in[2] & B_in[2]) || ((A_in[2] ^ B_in[2]) & C[1]);
    assign C[3] = (A_in[3] & B_in[3]) || ((A_in[3] ^ B_in[3]) & C[2]);
    assign CO = C[3];

endmodule