回溯-组合总和

LeetCode链接

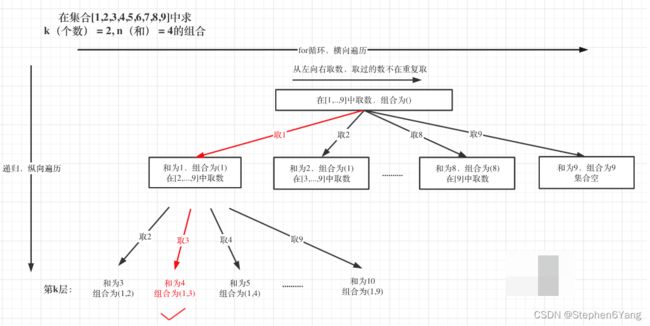
本题k相当于树的深度，9（因为整个集合就是9个数）就是树的宽度。

例如 k = 2，n = 4的话，就是在集合[1,2,3,4,5,6,7,8,9]中求 k（个数） = 2, n（和） = 4的组合。

选取过程如图：

回溯三部曲

确定递归函数参数

需要一维数组path来存放符合条件的结果，二维数组result来存放结果集。
这里我依然定义path 和 result为全局变量。
至于为什么取名为path？从上面树形结构中，可以看出，结果其实就是一条根节点到叶子节点的路径。

List<List<Integer>> result = new ArrayList<List<Integer>>();
LinkedList<Integer> path = new LinkedList<Integer>();

接下来还需要如下参数：

targetSum（int）目标和，也就是题目中的n。
k（int）就是题目中要求k个数的集合。
sum（int）为已经收集的元素的总和，也就是path里元素的总和。
startIndex（int）为下一层for循环搜索的起始位置。

确定终止条件

在上面已经说了，k其实就已经限制树的深度，因为就取k个元素，树再往下深了没有意义。

所以如果path.size() 和 k相等了，就终止。

如果此时path里收集到的元素和（sum） 和targetSum（就是题目描述的n）相同了，就用result收集当前的结果。

 if (sum > n) return;
        if (path.size() == k){
            if (sum == n){
                result.add(new ArrayList<>(path));
                return;
            }
        }

单层搜索过程

处理过程就是 path收集每次选取的元素，相当于树型结构里的边，sum来统计path里元素的总和。

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;

//leetcode submit region begin(Prohibit modification and deletion)
class Solution {
List result = new ArrayList();
LinkedList path = new LinkedList();
public List combinationSum3(int k, int n) {
backTrack(k,n,1,0);
return result;
}

public void backTrack(int k, int n, int startIndex, int sum){

    if (sum > n) return;
    if (path.size() == k){
        if (sum == n){
            result.add(new ArrayList<>(path));
            return;
        }
    }

    for (int i = startIndex; i <= 9 - (k-path.size()) + 1; i++) {
        sum += i;
        path.add(i);
        backTrack(k,n,i+1,sum);
        sum -= i;
        path.removeLast();
    }
}

}