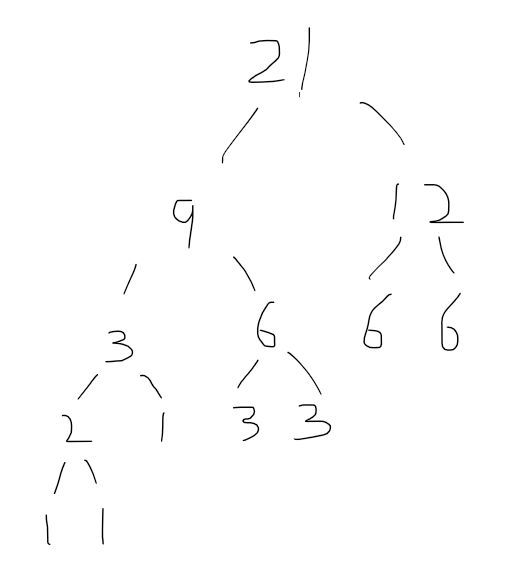7-1 哈夫曼编码 (PTA-数据结构)
给定一段文字,如果我们统计出字母出现的频率,是可以根据哈夫曼算法给出一套编码,使得用此编码压缩原文可以得到最短的编码总长。然而哈夫曼编码并不是唯一的。例如对字符串"aaaxuaxz",容易得到字母 'a'、'x'、'u'、'z' 的出现频率对应为 4、2、1、1。我们可以设计编码 {'a'=0, 'x'=10, 'u'=110, 'z'=111},也可以用另一套 {'a'=1, 'x'=01, 'u'=001, 'z'=000},还可以用 {'a'=0, 'x'=11, 'u'=100, 'z'=101},三套编码都可以把原文压缩到 14 个字节。但是 {'a'=0, 'x'=01, 'u'=011, 'z'=001} 就不是哈夫曼编码,因为用这套编码压缩得到 00001011001001 后,解码的结果不唯一,"aaaxuaxz" 和 "aazuaxax" 都可以对应解码的结果。本题就请你判断任一套编码是否哈夫曼编码。
输入格式:
首先第一行给出一个正整数 N(2≤N≤63),随后第二行给出 N 个不重复的字符及其出现频率,格式如下:
c[1] f[1] c[2] f[2] ... c[N] f[N]
其中c[i]是集合{'0' - '9', 'a' - 'z', 'A' - 'Z', '_'}中的字符;f[i]是c[i]的出现频率,为不超过 1000 的整数。再下一行给出一个正整数 M(≤1000),随后是 M 套待检的编码。每套编码占 N 行,格式为:
c[i] code[i]
其中c[i]是第i个字符;code[i]是不超过63个'0'和'1'的非空字符串。
输出格式:
对每套待检编码,如果是正确的哈夫曼编码,就在一行中输出"Yes",否则输出"No"。
注意:最优编码并不一定通过哈夫曼算法得到。任何能压缩到最优长度的前缀编码都应被判为正确。
输入样例:
7
A 1 B 1 C 1 D 3 E 3 F 6 G 6
4
A 00000
B 00001
C 0001
D 001
E 01
F 10
G 11
A 01010
B 01011
C 0100
D 011
E 10
F 11
G 00
A 000
B 001
C 010
D 011
E 100
F 101
G 110
A 00000
B 00001
C 0001
D 001
E 00
F 10
G 11
输出样例:
Yes
Yes
No
No提交结果:
思路分析:
哈夫曼树,哈夫曼编码,还没启动就会劝退很多人。此处学习心得代码,在博主发这个博文之前还没更新,很快就会看到的!!!
此题难度比较中肯,难度主要在对于题意的理解(文章内容说了一大堆关于什么是哈夫曼编码,什么是前缀码之类的内容,可以理解一下,方便我们下面开始堆砌),主要在于对于输入输出内容的理解。输入格式直接看样例即可,输出内容就是检测是否是哈夫曼编码,根据是否来输出yes和no。
那么,我们理解题意的关键在于“怎么判断是否为哈夫曼编码”,是哈夫曼编码的要求有二,其一是,该编码为前缀编码;其二是来自于哈夫曼树。第一个要求可以通过遍历两个字符的编码来实现(后文会讲),第二个要求需要将字符还原成“在树上的状态”,咱们来拿样例举例子从头分析上面的内容:(按照我们学过的内容,不难手绘出这棵哈夫曼树)
1.创建哈夫曼树
首先,我们来创建一棵哈夫曼树,这里具体代码可以去老师课上学习中得来,下面我复现了一下,可以直接复制使用。(固定算法,注意不要抄丢代码,否则会发生意想不到的错误)
typedef struct {
char ch;
int weight;
int parent;
int lchild;
int rchild;
}HufmTree;
//num为带权结点数,即“叶子”,roads = 2*num + 1容纳叶子的父母等
void Huffman(HufmTree tree[],int num,int roads){
int i,j,p1,p2;
int small_1,small_2;
for(i = 1;i<=roads;i++){
tree[i].parent = 0;
tree[i].lchild = tree[i].rchild = 0;
}
for(i = num+1;i<=roads;i++){
p1 = p2 = 1;
small_1 = small_2 = Maxval;
for(j = 1;j<=i-1;j++){
if(tree[j].parent == 0){
if(tree[j].weight 2.满足哈夫曼编码
要满足是哈夫曼编码,首先需要满足其可由构造一棵哈夫曼树得出,而哈夫曼树又是带权路径长度最小的二叉树,所以这里的带权路径长度之和就成了一个线索,即我们需要确认每组编码的带权路径长度,这里就必须和我们上面构建好的一棵哈夫曼树的权值来比较。问题就到了如何求带权路径长度。
这里有个捷径,数据结构课老师提出大意为:哈夫曼树上非叶子结点的结点的权值相加等于带权路径长度(太妙了)。所以下面通过这个方式,快速求得了权值(当然,我们仍然可以用传统方法,在给每个带权叶子创建哈夫曼树的途中求出每个带权叶子所在的层,简单来说就是:每个叶子的权值 * 所在层数 的求和)。
下面是代码(前面已经明白了,数组tree中,从num+1开始就不是叶子结点了,而是它们的父母。该处代码非常简洁):
int HuffmanVal(HufmTree tree[], int num){
int val = 0;
for (int i = num+1;i<=num*2-1;i++){
val = val + tree[i].weight;
}
return val;
} 比对权值之后,如果权值不正确,就可以直接输出No,但是还不够,存在权值正确,但是不满足前缀码的情况,此时就要用到非常丑陋的字符串比对:(1为不是哈夫曼编码,0为是哈夫曼编码,此处具体返回大意可见主函数)
int JudgePrefixCode(char ch1[],char ch2[]){
int len1 = strlen(ch1);
int len2 = strlen(ch2);
for (int i = 0; i < len2 && i3.主函数实现
此题输入内容比较冗杂,甚至需要多个getchar();来吸收回车。就此,我们的主函数也写了很长(为便于理解,我在写完的时候有些地方的printf检测函数并没有被删除,而是被注释掉,同学们可以将注释取消,看看效果),然后就是正常的根据要求写代码,以及对于函数的调用。
#include
#include
#define Maxval 32767
typedef struct {
char ch;
int weight;
int parent;
int lchild;
int rchild;
}HufmTree;
typedef struct {
char ch;
char code[64];
}TestNode;
int main(){
int num;
scanf("%d",&num);
getchar();
int roads = 2*num + 1;
HufmTree tree[2*num + 2];
for(int i=0;i<=2*num+1;i++){
tree[i].weight = -1;
tree[i].ch = '-';
}
for(int i=1;i<=num;i++){
scanf("%c %d",&tree[i].ch,&tree[i].weight);
getchar();
}
Huffman(tree,num,roads);
/*for (int i = 0; i <= 2 * num - 1; i++) {
printf("Node %d: ch = %c, weight=%d, parent=%d, lchild=%d, rchild=%d\n",i,tree[i].ch, tree[i].weight, tree[i].parent, tree[i].lchild, tree[i].rchild);
}*/
int val = HuffmanVal(tree,num);
//printf("%d\n",val);
int n;
scanf("%d",&n);
getchar();
TestNode exam[num+1];
int flags[n];
for(int k = 0;k 大功告成!
代码展示:
//
// Created by DDD on 2023/12/4.
//
#include
#include
#define Maxval 32767
typedef struct {
char ch;
int weight;
int parent;
int lchild;
int rchild;
}HufmTree;
typedef struct {
char ch;
char code[64];
}TestNode;
void Huffman(HufmTree tree[],int num,int roads){
int i,j,p1,p2;
int small_1,small_2;
for(i = 1;i<=roads;i++){
tree[i].parent = 0;
tree[i].lchild = tree[i].rchild = 0;
}
for(i = num+1;i<=roads;i++){
p1 = p2 = 1;
small_1 = small_2 = Maxval;
for(j = 1;j<=i-1;j++){
if(tree[j].parent == 0){
if(tree[j].weight 下面图以及排序的内容可能会更难,大的还在后面呢!
冲刺六级中