一文读懂苹果的差分隐私技术原理

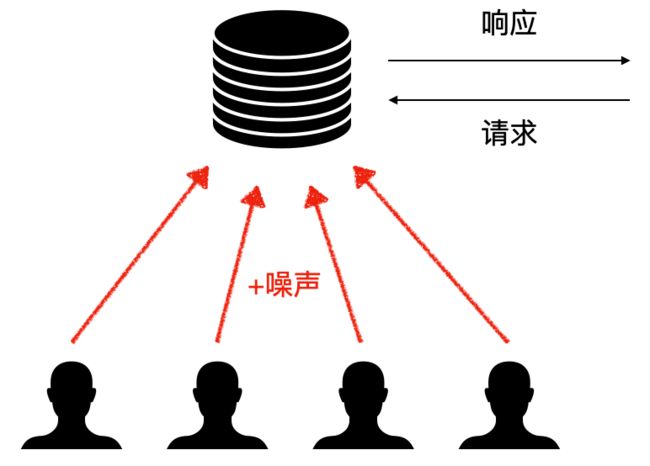
在 2016 年 6 月份的苹果 WWDC 大会上提到了一项差分隐私技术（Differential Privacy），其作用是对用户的数据进行扰动，然后上传到苹果服务器。苹果能通过这些扰动过的数据计算出用户群体的行为模式，但是对每个用户个体的数据却无法解析。

苹果通过采用差分隐私技术，实现了在不得到用户原始数据的前提下，学习用户行为。如果你想知道“数据可用不可见”背后的技术，就跟着我们一起来学习下苹果的差分隐私技术背后的原理吧！

一、简介

差分隐私是一种数据隐私保护技术，它通过在数据中引入随机化扰动的手段来保护隐私。简单来说，扰动后的数据是无法精确地推断出其原始值。同时，它允许对随机化后数据进行统计分析，保证了数据的有用性。差分隐私提供了衡量隐私的严格数学定义，是近些年来业界常见的一种隐私保护技术。

1.1 差分隐私应用场景

苹果使用本地化差分隐私（Local Differential Privacy）技术来收集用户设备上的信息，其部署的产品见下表 [1, 2]。

产品名称	用途
QuickType suggestions	学习热门新词汇，用于键盘打字预测
Emoji suggestions（Emoji 预测）	学习流行表情包趋势，预测用户使用的表情包
Lookup Hints（搜索提示）	iOS 搜索框提示
Safari Energy Draining Domains & Crashing Domains	统计电量消耗大（高 CPU、高内存使用）的网站、易崩溃的网站
Safari Autoplay Intent Detection	统计用户倾向于自动播放且不静音的网站
Health Type Usage	流行的健康数据类型（睡眠、心率、卡路里等）统计

1.2 本地化差分隐私

在本地化差分隐私框架中，用户在上传的原始数据中添加噪声（扰动），服务器则无法知道用户的真实数据。这项技术最早是由 Warner 提出的随机响应（Randomized response）[3]。

本地化差分隐私技术可用于联合统计，比如计算平均数、中位数、频率直方图等。其算法框架（E-R-A-P）一般分为四个步骤：

1. 编码（Encoding, E）
2. 随机化（Randomizing, R）
3. 聚合（Aggregation, A）
4. 后处理（Post-processing, P）

用户端进行编码与随机化，保证传输的数据是扰动后的；服务器端进行聚合与后处理，得到相应的统计量。

二、苹果的方案

苹果的本地化差分隐私方案参见 [2, 4, 5]，其中 [4, 5] 是专利。这里介绍 [2] 中方案的简易版本，以统计表情包的频率直方图为例。

2.1 用户端

依照上面提到的 算法框架（E-R-A-P），用户端需要在上传数据之前对做原始数据做 编码(E) 和 随机化®。

编码(E)：编码是为了后续的随机化和聚合步骤。苹果的编码采用哈希表的方式，初始表中的元素均为“-1”。然后通过哈希函数$h$将元素$d$（使用频率最高的表情包）映射到位置$h(d)$，并标记“1”。假设哈希表的长度为$m$（聚合时会用到该参数）。

随机化 ®：随机化是差分隐私中的关键步骤，保证了数据的隐私性。由于编码后的数据都是“1”和“-1”，让每个比特以设定的概率$p$翻转，即“1”变为“-1”或“-1”变为“1”。其中$p=1/(1+e^{ϵ/2})$，$ϵ$称为隐私预算，将在 第 2.4 节阐述。

2.2 服务器端

依照上面提到的 算法框架（E-R-A-P），服务器端需要在接收到数据后对做“扰动”后的数据做 聚合(A) 和 后处理§。

聚合 (A)：由于每个用户上传的数据都是扰动后的，聚合可以消除部分噪声的影响。假设共有$n$个用户，服务器收到用户$i$的哈希表为$v^{(i)}$。服务器首先计算：

$x^{(i)}=\frac{c_{ϵ}{v}^{(i)}+1}{2}$，其中$c_{ϵ}=\frac{e^{ϵ/2}+1}{e^{ϵ/2}-1}$

然后将所有$x$的对应位置累加，得到$M$，即

$$M=\sum _{i=1}^n{x}^{(i)}$$

则统计元素$d$的个数$\tilde{f}(d)$的公式如下，其中$M_{h(d)}$表示$M$在位置$h(d)$的值

$$\tilde{f}(d)=\frac{m}{m-1}(M_{h(d)}-\frac{n}{m})$$

可以证明$\tilde{f}(d)$为$f(d)$的无偏估计，即$\mathbb{E}[\tilde{f}(d)]=f(d)$，其中$f(d)$为元素$d$的真实个数。这意味着估计值的期望与真实值的偏差为零，保证了估计值的无偏性。

后处理 §：在不同应用场景中，计算的统计量可能有先验知识，比如取值范围的限制（如大于 0），或者保持加和不变（如统计个数），这时就需要进行后处理操作。差分隐私的性质使得任何后处理操作均不影响其结果的隐私性。

2.3 其他技术

数据隐私保护需要考虑的方面很多，仅使用差分隐私技术无法解决所有的问题。苹果在方案中还使用了其他技术来保护数据隐私，例如数据脱敏、通信加密、访问控制等。

1. 用户上传的数据已移除设备标识符、时间戳等信息
2. 用户与服务器通信使用 TLS 协议，即数据加密传输
3. 服务器收到用户数据后首先移除 IP 地址、时间戳等 meta 信息，并将数据顺序打乱（shuffle）
4. 数据聚合在受限访问环境中执行
5. 数据只在苹果内部流通，且苹果的员工不能随意访问数据

2.4 隐私预算

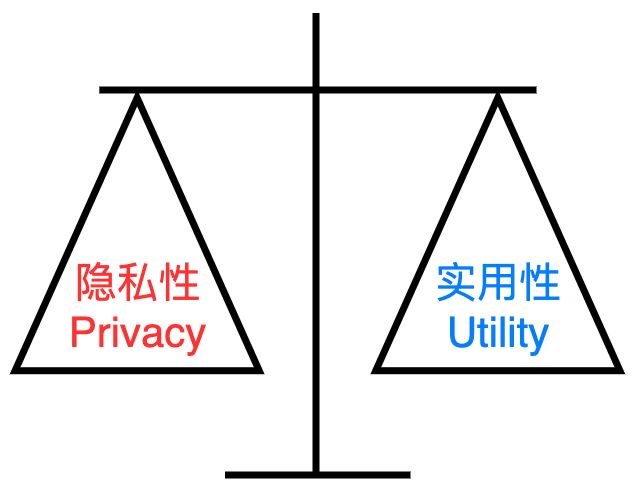
看到这里大家应该明白了，差分隐私是通过在增加噪声（扰动）来实现隐私保护，但由于扰动增加，聚合的结果会变得不精确（统计量的方差增大）。所以下面介绍平衡算法的隐私性和实用性的隐私预算$ϵ$。

在差分隐私中隐私预算$ϵ$的选取会同时影响算法的隐私性与实用性，称为 Privacy-Utility 之间的权衡（trade-off）。较小的隐私预算$ϵ$意味着较强的隐私保护能力。例如，数据比特随机化扰动的概率$p=1/(1+e^{ϵ/2})$，减小$ϵ$的取值会使得$p$增大，因此隐私泄漏的风险会降低，但此举也会影响结果的精确性。

而且，虽然数据添加了差分隐私扰动，但同一用户会不断地上传新数据，根据差分隐私的串型组合定理，隐私预算$ϵ$会随着时间累积逐步增加。因此，苹果限制了用户每天上传数据的最大次数，并表示数据最多只会留存三个月。

产品名称	隐私预算$ϵ$的取值	数据最多上传次数 / 每天
QuickType suggestions	8	2
Emoji suggestions（Emoji 预测）	4	1
Lookup Hints（搜索提示）	4	2
Safari Energy Draining Domains & Crashing Domains	4	2
Safari Autoplay Intent Detection	8	2
Health Type Usage	2	1

有研究 [6] 指出，苹果应该解释是如何设置隐私预算$ϵ$的取值的，告知用户并将其透明化。例如，虽然 Emoji 产品中宣称的隐私预算$ϵ$取值为 1，但通过代码逆向工程后发现其取值为 2（iOS 10.1.1 和 MacOS 10.12.3 版本的数据）。而且，隐私预算随时间累积也是其方案存在的一个重要问题。

三、方案优化

第 2 节中描述的是方案的简易版，而苹果的方案针对通信、统计量的精确性、场景适配等均做了优化 [2]如下：

1. 为了减少哈希碰撞的影响，实际有$k$个哈希函数，每个用户在编码时随机选择一个，并将选择的哈希函数告诉服务器。服务器则构建$k$个哈希表，然后进行聚合计算。
2. 为了降低通信量，苹果的方案中对编码后的数据进行了阿达马变换（Hadamard transform），并通过采样的方式，随机选择 1 比特的数据发送到服务器。这样不仅可以降低通信量，而且不会增加统计值的方差。
3. 表情包的数据一般是固定的，但在一些场景下，用户数据是无法预知的。比如学习热门新词汇，统计网站。苹果对此采用了 Sequence Fragment Puzzle 技术，并设计了本地化差分隐私的方案。

四、无偏估计证明

这里依旧是按照 算法框架（E-R-A-P）顺序进行讲解，证明$\tilde{f}(d)$是$f(d)$的无偏估计。

4.1 编码

用户$i$的哈希表为$v^{(i)}$，元素$d$在表中的映射位置为$h(d)$，其对应编码的取值为$v_{h(d)}^{(i)}$。用户$i$上传的元素为$d^{(i)}$，其对应位置的编码值为“1”，哈希表的其余位置为“-1”。因此当$d^{(i)}=d$时，$v_{h(d)}^{(i)}$的期望为

$$\mathbb{E}[v_{h(d)}^{(i)}]=1$$

由于哈希表可能会存在碰撞（冲突），即不同元素标记到了同一位置。假设数据映射到不同位置的概率是相同的，则碰撞概率为 $1/m$。因此当$d^{(i)}\ne d$时，$v_{h(d)}^{(i)}$ 的期望为

$$\mathbb{E}[v_{h(d)}^{(i)}]=\frac{1}{m}\cdot 1+(1-\frac{1}{m})\cdot (-1)=\frac{2}{m}-1$$

因此$v_{h(d)}^{(i)}$的期望为

$$\mathbb{E}[v_{h(d)}^{(i)}]=\mathbb{I}\{d^{(i)}=d\}+(\frac{2}{m}-1)\mathbb{I}\{d^{(i)}\ne d\}$$

4.2 随机化

随机化时比特翻转的概率为$p=1/(1+e^{ϵ/2})$。假设随机变量$B\in \{-1,1\}$，$\mathrm{Pr}(B=-1)=p$。

$\mathbb{E}[B]=p\cdot (-1)+(1-p)\cdot 1=1-2p=\frac{e^{ϵ/2}-1}{e^{ϵ/2}+1}=\frac{1}{c_{ϵ}}$，其中$c_{ϵ}=\frac{e^{ϵ/2}+1}{e^{ϵ/2}-1}$

用户$i$随机化后的哈希表为$B{v}^{(i)}$，元素$d$在表中的编码值为$B{v}_{h(d)}^{(i)}$。

$$\mathbb{E}[B{v}_{h(d)}^{(i)}]=\mathbb{E}[B]\cdot \mathbb{E}[v_{h(d)}^{(i)}]=\frac{1}{c_{ϵ}}\mathbb{E}[v_{h(d)}^{(i)}]$$

4.3 聚合

服务器对随机化后的哈希表进行转换，即计算$x$。元素$d$在用户$i$哈希表转换后映射位置的编码值为$x_{h(d)}^{(i)}$，

$$x_{h(d)}^{(i)}=\frac{c_{ϵ}B{v}_{h(d)}^{(i)}+1}{2}$$

当$d^{(i)}=d$时，$\mathbb{E}[c_{ϵ}B{v}_{h(d)}^{(i)}]=1$，故

$$\mathbb{E}[x_{h(d)}^{(i)}]=1$$

当$d^{(i)}\ne d$时，$\mathbb{E}[c_{ϵ}B{v}_{h(d)}^{(i)}]=\frac{2}{m}-1$，故

$$\mathbb{E}[x_{h(d)}^{(i)}]=\frac{1}{m}$$

因此$x_{h(d)}^{(i)}$的期望为

$$\mathbb{E}[x_{h(d)}^{(i)}]=\mathbb{I}\{d^{(i)}=d\}+\frac{1}{m}\mathbb{I}\{d^{(i)}\ne d\}$$

将所有的$x$累加，计算$M$，元素$d$在$M$中映射位置的编码值为$M_{h(d)}$，

$$M_{h(d)}=\sum _{i=1}^n{x}_{h(d)}^{(i)}$$

计算其期望，其中$f(d)$是元素$d$的真实个数

$$\begin{array}{rl}\mathbb{E}[M_{h(d)}]& =\mathbb{E}\left[\sum _{i=1}^n{x}_{h(d)}^{(i)}\right]\\ & =\sum _{i=1}^n\mathbb{I}\{d^{(i)}=d\}+\frac{1}{m}\sum _{i=1}^n\mathbb{I}\{d^{(i)}\ne d\}\\ & =f(d)+\frac{1}{m}(n-f(d))\\ & =\frac{m-1}{m}f(d)+\frac{n}{m}\end{array}$$

由于$\tilde{f}(d)$是元素$d$个数的统计值，其计算公式为

$$\tilde{f}(d)=\frac{m}{m-1}(M_{h(d)}-\frac{n}{m})$$

所以

$$\mathbb{E}[\tilde{f}(d)]=f(d)$$

即$\tilde{f}(d)$是$f(d)$的无偏估计。

统计量的方差小才意味着估计的精确性高。关于统计量$\tilde{f}(d)$方差的证明请参考。

以上通过公式推导的方式证明了苹果采用的「差分隐私」算法的准确性，可以实现在“数据可用不可见”的情况下实现统计计算。

五、最后

看似“高不可攀”的差分隐私技术，其实早已走进了我们的日常生活和工作中，为我们的个人隐私保驾护航。

本文通过通俗易懂的图文和严谨的公式推导，讲解了苹果的差分隐私技术原理，希望能够勾起你对隐私计算技术的兴趣。最后，如果你还有什么想了解的隐私计算相关技术，欢迎留言告诉我们！

PrimiHub 一款由密码学专家团队打造的开源隐私计算平台。我们专注于分享数据安全、密码学、联邦学习、同态加密等隐私计算领域的技术和内容。

参考文献

[1] Apple Differential Privacy Technical Overview. https://www.apple.com/privacy/docs/Differential_Privacy_Overview.pdf

[2] Differential Privacy Team, Apple. “Learning with privacy at scale.” (2017). https://docs-assets.developer.apple.com/ml-research/papers/learning-with-privacy-at-scale.pdf

[3] Warner, Stanley L. “Randomized response: A survey technique for eliminating evasive answer bias.” Journal of the American Statistical Association 60, no. 309 (1965): 63-69. https://www.jstor.org/stable/2283137

[4] Thakurta, Abhradeep Guha, Andrew H. Vyrros, Umesh S. Vaishampayan, Gaurav Kapoor, Julien Freudiger, Vivek Rangarajan Sridhar, and Doug Davidson. “Learning new words.” Granted US Patents 9645998 (2017). https://patents.google.com/patent/US9645998

[5] Thakurta, Abhradeep Guha, Andrew H. Vyrros, Umesh S. Vaishampayan, Gaurav Kapoor, Julien Freudinger, Vipul Ved Prakash, Arnaud Legendre, and Steven Duplinsky. “Emoji frequency detection and deep link frequency.” Granted US Patents 9705908 (2017). https://patents.google.com/patent/US9705908

[6] Tang, Jun, Aleksandra Korolova, Xiaolong Bai, Xueqiang Wang, and Xiaofeng Wang. “Privacy loss in apple’s implementation of differential privacy on macos 10.12.” arXiv preprint arXiv:1709.02753 (2017). https://arxiv.org/pdf/1709.02753