C++STL的stack和queue(超详解)

前言

栈和队列这一块其实有数据结构的基础，学起来非常简单。

stack

栈的成员函数就这么写，除了emplace其他都已经非常熟悉了。

stack没有迭代器吗？
没有，因为栈已经不是容器了，它是容器适配器。给它一个迭代器还能保证先进先出这些吗？不能。

stack跟我们之前学的list其实很不太一样。

模板参数不同。

先快速用一下stack，让它跑起来。

void test_stack()
{
  stack<int> st;
	st.push(1);
	st.push(2);
	st.push(3);
	st.push(4);

	while (!st.empty())
	{
		cout << st.top() << " ";
		st.pop();
	}
	cout << endl;
}

stack的模拟实现

栈的实现有两种方式。
1.数组栈，尾部当作栈顶。
2.链表栈，头部当作栈顶。
数组栈更有优势一点。

传统的写法，无非就是搞一个数组，不够了就扩容。
我们这里用一个适配器模式。

适配器的本质是什么？
现实生活中，我们的充电头也叫电源适配器。电源适配器是干嘛的？是生产电源的吗？
其实是用来变压的。
所以适配器的本质是用来转换的，把原来的东西给转换过来。

容器适配器，它不是自己存储数据，它是把已有的东西进行转换。

我们要实现一个顺序栈，链表栈，我们需要自己写吗？
我们可以拿一个已有的容器封装，这样写起来更简单。

为什么叫适配模式呢？
总结出来写代码的固定方式。

那怎么实现呢？
我们实现一个数组栈，链式栈，我们可以拿已有的容器封装，这样写起来更简单

但是上面这还不是适配，还要可以转换。
所以是这样写的，再增加一个模板参数，Container,他具体是啥我也不知道，但是它肯定是符合我们要求的容器。

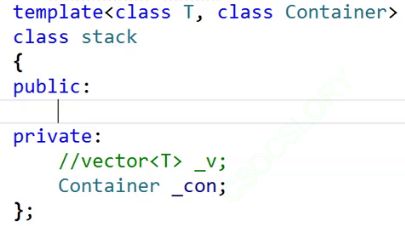
要实现顺序栈，传vector.
要实现链表栈，传list.

namespace but
{
	
	template<class T, class Container>
	class stack
	{
	public:
		void push(const T& x)
		{
			_con.push_back(x);
		}

		void pop()
		{
			_con.pop_back();
		}

		const T& top()
		{
			return _con.back();
		}

		size_t size()
		{
			return _con.size();
		}

		bool empty()
		{
			return _con.empty();
		}

	private:
		//vector _v;
		Container _con;
	};

	void test_stack()
	{
	
		stack<int, vector<int>> st;//顺序栈
		//stack> st;//链式栈
		//stack st //缺省类型
		st.push(1);
		st.push(2);
		st.push(3);
		st.push(4);

		while (!st.empty())
		{
			cout << st.top() << " ";
			st.pop();
		}
		cout << endl;
	}
}

还可以给缺省类型。

template<class T, class Container= vector<T>>

函数传参如果不从右往左会有歧义。

假设传两个参数，你就不知道传给谁了。

栈的题目

最小栈

接下来我们做题来加深一下对stack的理解。
最小栈

思路

首先定义两个栈，一个栈是正常的栈，实现正常的操作。
我们用另一个栈是最小栈，来实现O(1)检索到最小元素的栈。

这里要不要写那4个默认成员函数？

不用。

push
如果是空栈或者需要push的数据小于最小栈栈顶元素，我们就push.否则最小栈不做处理。

注意，如果需要push的数据等于栈顶元素也要push，否则pop的时候会把最小值也pop掉

pop
如果最小栈的栈顶元素和正常栈的栈顶元素相等我们就pop

class MinStack {
public:
//不用写
    MinStack() {
       
    }
    void push(int val) {
        _st.push(val);
        if (_minst.empty() || val <= _minst.top())
        {
            _minst.push(val);
        }
    }
    void pop() {
        if (_minst.top() == _st.top())
        {
            _minst.pop();
        }
        _st.pop();
    }
    int top() {
        return _st.top();
    }
    int getMin() {
        return _minst.top();
    }
private:
    stack<int> _st;
    stack<int> _minst;
};

优化

如果是这样那不是很浪费。

可以这样优化，每个地方不是存一个值而是存一个结构。

给大家看一下结构，具体实现就先不实现了。

stack<int> _st;
struct Data
{
	int _val;
	int _count;
}
stack<Date> _minst;

这就是模板的好处，如果没有模板，那自己还需要再写一个栈。

JZ31 栈的压入、弹出序列

栈的压入、弹出序列


这道题稍有不慎就会写的很复杂，如果想清楚了也挺简单的。

不匹配的一种情况

思路
这道题有很多种思路，最简单的就是用一个栈模拟入栈出栈的过程。
如果能模拟出来就匹配了，如果模拟不出来就不行。

所以我们的重点在于模拟这个栈。

先要第一个出4，那就入数据1234。只要不匹配就入数据。

下一个出5，不匹配继续入

再看下一个要出的数据是不是栈顶的元素，是就直接出。

如果能把入栈序列走完，出栈序列也走完，那就匹配了。

以pushi为主要的，因为popi不一定能走到结尾。
第一步，入栈
第二步，判断是否要出栈(注意不一定只出一次)

凡是这样写一定要小心，栈出了一个，然后栈空了。

空栈调用会报错。

怎么样匹配？
两种方式
1.popi走到尾了
2.栈为空

150. 逆波兰表达式求值

逆波兰表达式求值

中缀表达式
我们平时写的式子都是中缀表达式。但是计算机对于中缀表达式没办法直接运算。
比如1+2*(3-2)，计算机遇到操作数的时候是不敢运算的，因为还涉及到优先级。

后缀表达式
所以我们先把优先级给确定出来。
后缀就是优先级已经按先后顺序确定了。

上面的这道题就是用后缀表达式求出结果？省去了中缀转后缀的过程，所以难度大大降低了。

运算后缀表达式
用一个栈就搞定了。

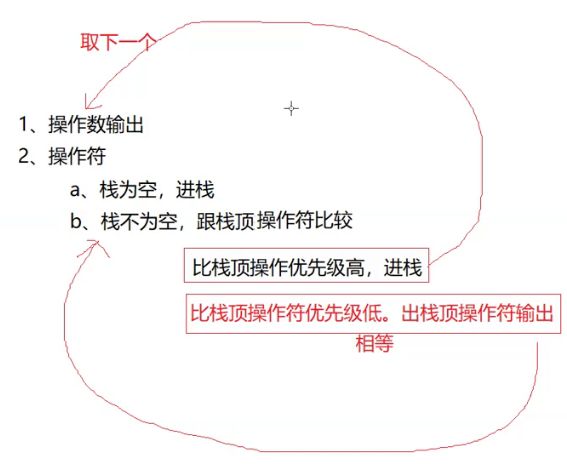
过程
操作数入栈

操作符计算
先出的是右操作数。计算，结果入栈。

最后

这道题不难，但是你要理解一个逆波兰表达式为什么可以这样算，你就要理解中缀怎么转后缀。

代码实现

怎么确定是操作数还是操作符？
这里有个小坑，如果操作不当，减号和负数会混。

最简单的方式是用一个字符串的比较就可以了
操作数入栈

操作符出栈，计算。

如何中缀转后缀？

注意，输出并不指的是打印，而是说把数据放到一个容器里保存起来。

跟栈顶操作符比较，优先级更高，不能直接输出，因为后面可能还有优先级更高的。

然后回到之前第一步，操作数输出

综上所述，我们便可以看到为什么后缀运算可以利用一个栈来进行模拟？
中缀转后缀的时候。
操作符出的时候，跟我相邻的两个数，就是要跟这个操作符的两个数运算，结果作为操作数又进行运算。
中缀转后缀就是这样转的，它的规则就是这样的。

操作符出了，我要让两个操作数一定是在我的前面。那我怎么找到最近的两个操作数呢？
栈的后进先出刚刚好

很巧很巧，像发明栈的大佬致敬。

真正麻烦处理的还是带括号的。
比如1 + 2*（4 - 5）+ 6/7；

可以尝试先把后缀表达式写出来。

flag的解决方式
flag0的时候正常处理。
flag1的时候说明遇到括号了。
下一个的运算符优先级是高。

不用flag的解决方式
这里就先不讲了。

queue的模拟实现

快速手搓。

namespace but
{
	template<class T, class Container = list<T>>
	class queue
	{
	public:
		void push(const T& x)
		{
			_con.push_back(x);
		}

		void pop()
		{
			_con.pop_front();
		}

		const T& front()
		{
			return _con.front();
		}

		const T& back()
		{
			return _con.back();
		}

		size_t size()
		{
			return _con.size();
		}

		bool empty()
		{
			return _con.empty();
		}

	private:
		Container _con;
	};

	void test_queue()
	{
		queue<int> q;
		q.push(1);
		q.push(2);
		q.push(3);
		q.push(4);

		while (!q.empty())
		{
			cout << q.front() << " ";
			q.pop();
		}
		cout << endl;
		
	}
}

队列还能不能用vector适配？
队列要头插尾删，vector不支持头删。如果强行用erase，效率有点低。

在实现队列的头文件里没有包括vector和list为什么还能用？
如果编译它是会报错的，但是编译器不编译它。.h是不会被编译的，它是在包含的地方展开，然后编译器向上找。

这样写就不行了

为什么?
因为c和c++编译的时候都有一个特点，他不会在整个文件里面找。一展开像上去找，找不到vector,因为vector在std里面，又没有指定std.

在命名空间里只有指定或者展开才能找到。

从string开始，只写.h,不写cpp,为什么？
从规范角度来说肯定要写的，模板不能这么写，这样写出来是有问题的。
你可以尝试用声明和定义分离写一下stack。

为什么又找不到vector?
stack.cpp这里展开.h，又找不到vector.

声明和定义分离会导致很多问题，他会导致链接错误。链接错误就是找不到定义。
模板不能声明和定义分离。