透析回溯的模板

关卡名	认识回溯思想	我会了✔️
内容	1.复习递归和N叉树，理解相关代码是如何实现的	✔️
	2.理解回溯到底怎么回事	✔️
	3.掌握如何使用回溯来解决二叉树的路径问题	✔️

回溯可以视为递归的拓展，很多思想和解法都与递归密切相关，在很多材料中都将回溯都与递归同时解释，例如本章2.1的路径问题就可以使用递归和回溯两种方法来解决。因此学习回溯时，我们对比递归来分析其特征会理解更深刻。
关于递归和回溯的区别，我们设想一个场景，某猛男想脱单，现在有两种策略：

• 1.递归策略：先与意中人制造偶遇，然后了解人家的情况，然后约人家吃饭，有好感之后尝试拉人家的手，没有拒绝就表白。
• 2.回溯策略：先统计周围所有的单身女孩，然后一个一个表白， 被拒绝就说“我喝醉了”，然后就当啥也没发生，继续找下一个。

其实回溯本质就这么个过程，请读者学习本章时认真揣摩这个过程。
回溯最大的好处是有非常明确的模板，所有的回溯都是一个大框架，因此透彻理解回溯的框架是解决一切回溯问题的基础。第一章我们只干一件事，那就是分析这个框架。
回溯不是万能的，而且能解决的问题也是非常明确的，例如组合、分割、子集、排列，棋盘等等，不过这些问题具体处理时又有很多不同，本章我们梳理了多个最为热门的问题来解释，请同学们认真对待。
回溯可以理解为递归的拓展，而代码结构又特别像深度遍历N叉树，因此只要知道递归，理解回溯并不难，难在很多人不理解为什么在递归语句之后要有个“撤销”的操作。 我们会通过图示轻松给你解释该问题。这里先假设一个场景，你谈了个新女朋友，来你家之前，你是否会将你前任的东西赶紧藏起来？回溯也一样，有些信息是前任的，要先处理掉才能重新开始。
回溯最让人激动的是有非常清晰的解题模板，如下所示，大部分的回溯代码框架都是这个样子，具体为什么这样子我们后面再解释。 

void backtracking(参数) {
        if (终止条件) {
            存放结果;
            return;
        }
        for (选择本层集合中元素（画成树，就是树节点孩子的大小）){
            处理节点;
            backtracking();
            回溯，撤销处理结果;
        }
    }

回溯是有明确的解题模板的，本章我们只干一件事——分析回溯的模板。

1 从N叉树说起

在解释回溯之前， 我们先看一下N叉树遍历的问题，我们知道在二叉树中，按照前序遍历的过程如下所示：

void treeDFS(TreeNode root) {
    if (root == null)
        return;
    System.out.println(root.val);
    treeDFS(root.left);
    treeDFS(root.right);  
}

class TreeNode{
   int val;
   TreeNode left;
   TreeNode right;
}

假如我现在是一个三叉、四叉甚至N叉树该怎么办呢？很显然这时候就不能用left和right来表示分支了，使用一个List比较好，也就是这样子：

class TreeNode{
   int val;
   List nodes;
}

遍历的代码：

public static void treeDFS(TreeNode root) {
    //递归必须要有终止条件
    if (root == null){
     return;
    }
 // 处理节点
    System.out.println(root.val);
 
    //通过循环，分别遍历N个子树
    for (int i = 1; i <= nodes.length; i++) {
        treeDFS("第i个子节点");
    }
}

 到这里，你有没有发现和上面说的回溯的模板非常像了？是的！非常像！既然很像，那说明两者一定存在某种关系。其他暂时不管，现在你只要先明白回溯的大框架就是遍历N叉树就行了。

2 为什么有的问题暴力搜索也不行

我们说回溯主要解决暴力枚举也解决不了的问题，什么问题这么神奇，暴力都搞不定？
看个例子：

LeetCode77 ：给定两个整数 n 和 k，返回 1 ... n 中所有可能的 k 个数的组合。例如，输入n=4，k=2，则输出：
[[2,4], [3,4], [2,3], [1,2], [1,3], [1,4]]

 首先明确这个题是什么意思，如果n=4，k=2，那就是从4个数中选择2个，问你最后能选出多少组数据。
这个是高中数学中的一个内容，过程大致这样：如果n=4，那就是所有的数字为{1,2,3,4}

• 1.先取一个1，则有[1,2]，[1,3]，[1,4]三种可能。
• 2.然后取一个2，因为1已经取过了，不再取，则有[2,3]，[2,4]两种可能。
• 3.再取一个3，因为1和2都取过了，不再取，则有[3,4]一种可能。
• 4.再取4，因为1，2，3都已经取过了，所以直接返回null。
• 5.所以最终结果就是[1,2]，[1,3]，[1,4]，[2,3]，[2,4]，[3,4]。

这就是我们思考该问题的基本过程，写成代码也很容易，双层循环轻松搞定：

int n = 4;
        for (int i = 1; i <= n; i++) {
            for (int j = i + 1; j <= n; j++) {
                System.out.println(i + " " + j);
            }
        }

假如n和k都变大，比如n是200，k是3呢？也可以，三层循环基本搞定：

int n = 200;
  for (int i = 1; i <= n; i++) {
       for (int j = i + 1; j <= n; j++) {
            for (int u = j + 1; u <= n; n++) {
               System.out.println(i + " " + j + " " + u);
        }
   }

 如何这里的K是5呢？甚至是50呢？你需要套多少层循环？甚至告诉你K就是一个未知的正整数k，你怎么写循环呢？这时候已经无能为例了？所以暴力搜索就不行了。
这就是组合类型问题，除此之外子集、排列、切割、棋盘等方面都有类似的问题，因此我们要找更好的方式。

3 回溯=递归+局部枚举+放下前任

我们继续研究LeetCode77题，我们图示一下上面自己枚举所有答案的过程。
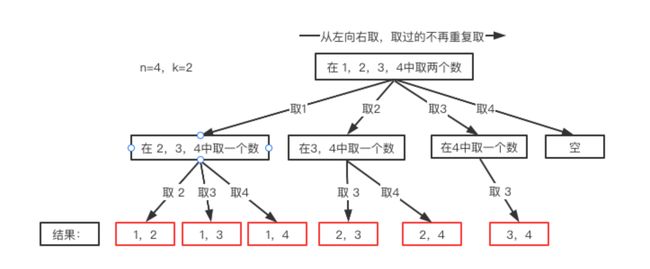
n=4时，我们可以选择的n有 {1,2,3,4}这四种情况，所以我们从第一层到第二层的分支有四个，分别表示可以取1，2，3，4。而且这里 从左向右取数，取过的数，不在重复取。 第一次取1，集合变为2，3，4 ，因为k为2，我们只需要再取一个数就可以了，分别取2，3，4，得到集合[1,2] [1,3] [1,4]，以此类推。
横向：

每次从集合中选取元素，可选择的范围会逐步收缩，到了取4时就直接为空了。
继续观察树结构，可以发现，图中每次访问到一次叶子节点(图中红框标记处)，我们就找到了一个结果。虽然最后一个是空，但是不影响结果。这相当于只需要把从根节点开始每次选择的内容（分支）达到叶子节点时，将其收集起来就是想要的结果。
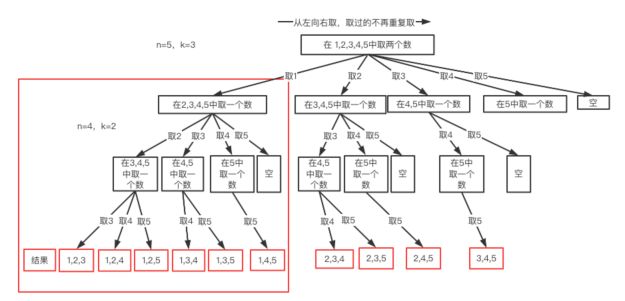
如果感觉不明显，我们再画一个n=5，k=3的例子：

从图中我们发现元素个数n相当于树的宽度（横向），而每个结果的元素个数k相当于树的深度（纵向）。所以我们说回溯算法就是一纵一横而已。再分析，我们还发现几个规律：
① 我们每次选择都是从类似{1,2,3,4}，{1,2,3,4,5}这样的序列中一个个选的，这就是局部枚举，而且越往后枚举范围越小。
② 枚举时，我们就是简单的暴力测试而已，一个个验证，能否满足要求，从上图可以看到，这就是N叉树遍历的过程，因此两者代码也必然很像。
③ 我们再看上图中红色大框起来的部分，这个部分的执行过程与n=4，k=2的处理过程完全一致，很明显这是个可以递归的子结构。
这样我们就将回溯与N叉树的完美结合在一起了。
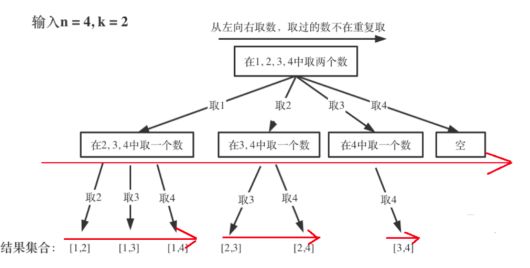
到此，还有一个大问题没有解决，回溯一般会有个手动撤销的操作，为什么要这样呢？继续观察纵横图：

我们可以看到，我们收集每个结果不是针对叶子结点的，而是针对树枝的，比如最上层我们首先选了1，下层如果选2，结果就是{1,2}，如果下层选了3，结果就是{1,3}，依次类推。现在的问题是当我们得到第一个结果{1,2}之后，怎么得到第二个结果{1,3}呢？
继续观察纵横图，可以看到，我可以在得到{1,2}之后将2撤掉，再继续取3，这样就得到了{1,3}，同理可以得到{1,4}，之后当前层就没有了，我们可以将1撤销，继续从最上层取2继续进行。
这里对应的代码操作就是先将第一个结果放在临时列表path里，得到第一个结果{1,2}之后就将path里的内容放进结果列表resultList中，之后，将path里的2撤销掉， 继续寻找下一个结果{1.3},然后继续将path放入resultLit，然后再撤销继续找。
现在明白为什么要手动撤销了吧，这个过程，我称之为"放下前任，继续前进"，后面所有的回溯问题都是这样的思路。
这几条就是回溯的基本规律，明白之后，一切都变得豁然开朗。如果还是不太明白，我们下一小节用更完整的图示解释该过程。
到此我们就可以写出完整的回溯代码了:

public List> combine(int n, int k) {
    List> resultList = new ArrayList<>();
    if(k<=0 || n path = new ArrayList<>();
    dfs(n,k,1,path,resultList);
    return resultList;
}
public void dfs(int n,int k,int startIndex,Deque path,List> resultList){
    // 递归终止条件是：path 的长度等于 k
    if(path.size()==k){
        resultList.add(new ArrayList<>(path));
        return;
    }
    // 针对一个结点，遍历可能的搜索起点，其实就是枚举
    for(int i=startIndex;i<=n;i++){
        // 向路径变量里添加一个数，就是上图中的一个树枝的值
        path.addLast(i);
        // 搜索起点要加1是为了缩小范围，下一轮递归做准备，因为不允许出现重复的元素
        dfs(n,k,i+1,path,resultList);
        // 递归之后需要做相同操作的逆向操作,具体后面继续解释
        path.removeLast();
    }
}

 上面代码还有个问题要解释一下：startIndex和i是怎么变化的，为什么传给下一层时要加1。
我们可以看到在递归里有个循环

for (int i = startIndex; i <= n; i++) {
    dfs(n,k,i+1,path,res);
 }

这里的循环有什么作用呢？看一下图就知道了，这里其实就是枚举，第一次n=4，可以选择1 ，2，3，4四种情况，所以就有四个分支，for循环就会执行四次： 

 

而对于第二层第一个，选择了1之后，剩下的元素只有2 ，3， 4了，所以这时候for循环就执行3次，后面的则只有2次和1次。

4 图解为什么有个撤销的操作

如果你已经明白上面为什么会有撤销过程，这一小节就不必看了。如果还是不懂，本节就用更详细的图示带你看一下。 回溯最难理解的部分是这个回溯过程，而且这个过程即使调试也经常会晕：

path.addLast(i);

dfs(n, k, i + 1, path, res);

path.removeLast();

为什么要remove呢？看下图，当第一层取1时，最底层的边从左向右依次执行“取2”、“取3”和“取4”，而取3的时候，此时list里面存的是上一个结果<1,2>，所以必须提前将2撤销，这就path.removeLast();的作用。
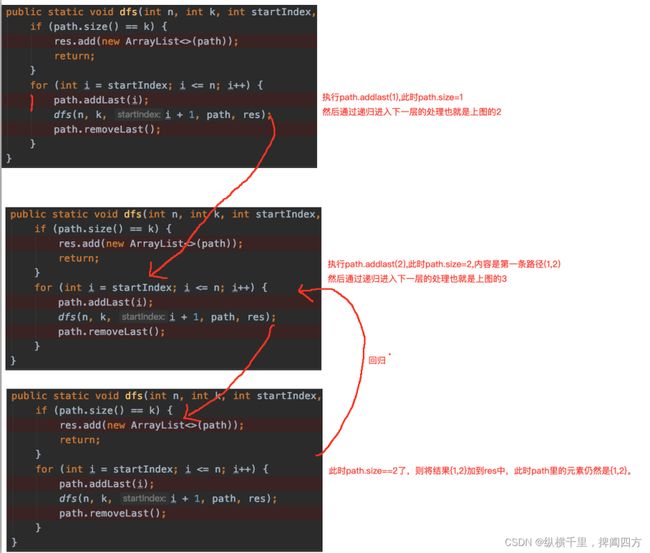
用我们拆解递归的方法，将递归拆分成函数调用，输出第一条路径{1,2}的步骤如下如下：

 

我们在递归章节说过，递归是“不撞南墙不回头”，回溯也一样，接下来画代码的执行图详细看一下其过程，图中的手绘的序号是执行过程:

然后呢？{1,2}输出 之后会怎么执行呢？回归之后，假如我们将remove代码去掉，也就是这样子：

注意上面的4号位置结束之后，当前递归就结束了，然后返回到上一层继续执行for循环体，也就是上面的5。进入5之后，接着开始执行第6步：path.addLast(i)了，此时path的大小是3，元素是{1,2,3}，为什么会这样呢？
因为path是一个全局的引用，各个递归函数共用的，所以当{1,2}处理完之后，2污染了path变量。我们希望将1保留而将2干掉，然后让3进来，这样才能得到{1,3}，所以这时候需要手动remove一下。
同样3处理完之后，我们也不希望3污染接下来的{1,4}，1全部走完之后也不希望1污染接下来的{2,3}等等，这就是为什么回溯里会在递归之后有一个remove撤销操作。

5 回溯热身—再论二叉树的路径问题

5.1 输出二叉树的所有路径

LeetCode257：给你一个二叉树的根节点root ，按任意顺序 ，返回所有从根节点到叶子节点的路径。
叶子节点是指没有子节点的节点。

示例：

输入：root = [1,2,3,null,5]

输出：["1->2->5","1->3"]

 

我们可以注意到有几个叶子节点，就有几条路径，那如何找叶子节点呢？我们知道深度优先搜索就是从根节点开始一直找到叶子结点，我们这里可以先判断当前节点是不是叶子结点，再决定是不是向下走，如果是叶子结点，我们就增加一条路径。
我们现在从回溯的角度来分析，得到第一条路径ABD之后怎么找到第二条路径ABE，这里很明显就是先将D撤销，然后再继续递归就可以了

 

class BinaryTreePaths {
    List ans = new ArrayList<>();
    public List binaryTreePaths(TreeNode root) {
        dfs(root,new ArrayList<>());
        return ans;
    }

    private void dfs(TreeNode root, List temp){
        if(root==null){
            return;
        }
        temp.add(root.val);
        //如果是叶子节点记录结果
        if(root.left==null&&root.right==null){
            ans.add(getPathString(temp));
        }
        dfs(root.left,temp);
        dfs(root.right,temp);
        temp.remove(temp.size()-1);
    }
    //拼接结果
    private String getPathString(List temp){
        StringBuilder sb = new StringBuilder();
        sb.append(temp.get(0));
        for(int i=1;i").append(temp.get(i));
        }
        return sb.toString();
    }
}

5.2 路径总和问题 

同样的问题是LeetCode113题，给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。

示例1：

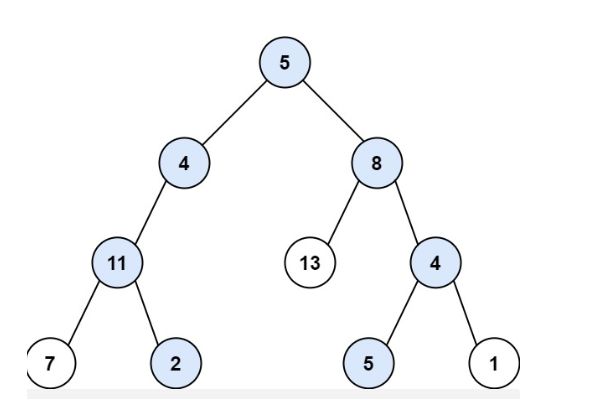
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22

输出：[[5,4,11,2],[5,8,4,5]]

本题怎么做呢？我们直接观察题目给的示意图即可，要找的targetSum是22。我们发现根节点是5，因此只要从左侧或者右侧找到targetSum是17的即可。继续看左子树，我们发现值为4，那只要从node(4)的左右子树中找targetSum是13即可，依次类推，当我们到达node(11)时，我们需要再找和为2的子链路，显然此时node(7)已经超了，不是我们要的,此时就要将node(7)给移除掉，继续访问node(2).
同样在根结点的右侧，我们也要找总和为17的链路，方式与上面的一致。完整代码就是：

class PathSum {
    List> res=new ArrayList<>();
    
    public List> pathSum(TreeNode root, int targetSum) {
        LinkedList path=new LinkedList<>();
        dfs(root,targetSum,path);
        return res;
    }
    
    public void dfs(TreeNode root,int targetSum,LinkedList path){
        if(root==null){
            return;
        }
        //这个值有很关键的作用
        targetSum-=root.val;
        path.add(root.val);
        if(targetSum==0 && root.left==null && root.right==null){
            res.add(new LinkedList(path));
        }
        dfs(root.left,targetSum,path);
        dfs(root.right,targetSum,path);
        path.removeLast();
    }
}