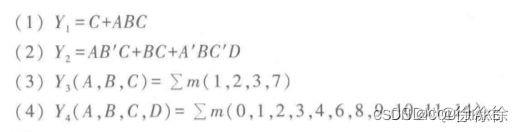12.12进制（原反补码，运算，进制转换），卡诺图化简，组合逻辑电路（竞争冒险，分析、设计方法），杂项

逻辑代数的基本定理和规则是用来处理逻辑函数的，其中包括以下几个重要的定理和规则：

1. 与门的性质：
- 同一律：A∧A=A
- 零律：A∧0=0
- 一律：A∧1=A

2. 或门的性质：
- 同一律：A∨A=A
- 零律：A∨0=A
- 一律：A∨1=1

3. 非门的性质：
- 否定律：¬(¬A)=A

4. 交换律：
- 与门交换律：A∧B=B∧A
- 或门交换律：A∨B=B∨A

5. 结合律：
- 与门结合律：A∧(B∧C)=(A∧B)∧C
- 或门结合律：A∨(B∨C)=(A∨B)∨C

6. 分配律：
- 分配律1：A∧(B∨C)=(A∧B)∨(A∧C)
- 分配律2：A∨(B∧C)=(A∨B)∧(A∨C)

7. 德摩根定律：
- 第一德摩根定律：¬(A∧B)=¬A∨¬B
- 第二德摩根定律：¬(A∨B)=¬A∧¬B

8. 吸收律：
- 吸收律1：A∨(A∧B)=A
- 吸收律2：A∧(A∨B)=A

这些定理和规则是逻辑代数中常用的基本原理，可以用来化简逻辑函数、简化逻辑电路等。

使用逻辑代数和卡诺图进行逻辑函数的化简可以按照以下步骤进行：

1. 根据逻辑函数的真值表或逻辑表达式，构建卡诺图。

2. 将卡诺图中具有相同数量的1的格子（方形）进行分组，每个分组代表了一个最小项

卡诺图，和之积，积之和

卡诺图当中，是与不变的量有关，而不是和在变的量有关

杂项

因为构成移位寄存器的触发器应该在一个时钟周期内只翻转一次，所以主从SR可以，基本和同步的不行。

奇偶校验中 1的个数要为奇数，若发送码中1的个数不为奇数，则监督码为1，否则为0.

verilog：过程内部语句：顺序语句，外部(module中)：并行语句，ep:assign语句。

移位寄存器的输出反馈到输入端可构成环形和扭环形计数器。

消除竞争冒险的方法：修改逻辑设计(增加冗余项)，引入选通脉冲，增加滤波电容。

最大项等于最小项取反

奇校验，监督码+原数中1的个数要为奇数。

进制转换。

按照相加进位方法不同可分为：逐位进位加法器和超前进位加法器。

Mealy时序电路的输出和电路状态和输入有关。

Moore时许电路的只和电路状态有关。

各种触发器中 只有RS触发器有约束条件 RS=0。

计数器一定包含存储元件(触发器)，存储元件就是存储一位二进制代码。

时序部件一定有储存器(即触发器)

P112 一个完整的时序逻辑电路由存储电路和组合逻辑电路构成，存储电路必不可少，组合逻辑电路是可选。两者都包含的是Mealy型，只包含存储电路的是Moore型。

T触发器的 低电平状态保持不变，高电平每个时钟周期翻转一次。

包含无关项的逻辑函数称为不完全确定的逻辑函数。

竞争冒险产生的主要原因是：时间延迟。

一个模块中可包含多个过程语句，多个过程语句是并行执行的，同时过程语句内部是顺序执行的。

时序逻辑电路任意时刻的输出状态 不只取决于该时刻的输入 还是取决于电路的原有状态

组合逻辑电路任意时刻输出只与当前输入有关

五.分析题。
题型1：

1.写出电路的驱动方程(激励方程),状态方程，输出方程，时钟方程。

一般都是由几个触发器和门组成，所以需要牢记触发器的状态方程。

2.画出波形图。

3.判断是否能自启动：先找到有效状态，若全为有效状态，没有无效状态则可以自启动。只包含一个环也可以自启动。

4.列出状态转换真值表。

左边自变量 从高位到低位，右边因变量，若有CLK，则最左边写CLK(从0开始 单位为1递增)。

4.分析电路实现的逻辑功能：

如果是计数器的话，先判断是同步还是异步：CLK接到一起是同步，否则是异步。

然后再判断是几进制，几个有效状态就是几进制。

然后再按照状态转换图判断是加法器还是减法器。

如果状态方程与输入有关，则说明是可控的计数器，然后分输入的情况来说明每个 的功能。

消除竞争冒险:

1.修改逻辑设计(增即冗余项)，可用卡诺图相切但不相交部分画个圈的项，即为需要增加的项。

对于Mealy 型电路 画状态转换图时，若有输入和输出，则要在转移边上写

输入/输出。

实现同一功能的Mealy型同步时序电路比Moore同步时序电路所需的状态数目更少。

1.画出状态转换图。

2.画出状态转换表，标出每个次态的上升，下降。

画出每个状态的次态卡诺图(上升记为1)。

写出驱动方程和时钟方程。

根据观察法得出每个状态的CLK。

画出电路图。

进制

1. 常用数制及其互换：
- 二进制（Binary）：由0和1组成的数制，逢二进一，最常用于计算机系统中。
- 十进制（Decimal）：由0-9十个数字组成的数制，逢十进一，是我们平时使用的常用数制。
- 八进制（Octal）：由0-7八个数字组成的数制，逢八进一。
- 十六进制（Hexadecimal）：由0-9和A-F（表示10-15）共十六个字符组成的数制，逢十六进一。常用于计算机系统中表示二进制数的简便方式。

这些数制之间的互换：
- 二进制和十进制的互换：二进制转换为十进制，可以将二进制数按权展开求和；十进制转换为二进制，可以将十进制数不断除以2，取余数，然后反向排列。
- 二进制和八进制的互换：二进制数先分组，每3位一组，然后将每组二进制数转换为对应的八进制数；八进制数中每个数字转换为对应的三位二进制数。
- 二进制和十六进制的互换：二进制数先分组，每4位一组，然后将每组二进制数转换为对应的十六进制数；十六进制数中每个数字转换为对应的四位二进制数。
- 十进制和八进制、十六进制的互换：十进制数可以通过不断除以8或16，取余数，然后反向排列转换为对应的八进制数或十六进制数；八进制数或十六进制数中每个数字转换为对应的三位或四位十进制数。

2. 符号数表示：
符号数是指能够表示正负的数。常见的符号数表示方法有：
- 原码表示法：用最高位表示符号位，0表示正数，1表示负数，其余位表示数值。
- 反码表示法：正数的反码与原码相同，负数的反码是对应正数的各位取反。
- 补码表示法：正数的补码与原码相同，负数的补码是对应正数的反码加1。

3. 数字与字符编码：
数字和字符之间的转换常用的编码方式有ASCII码和Unicode。
- ASCII码（American Standard Code for Information Interchange）是最常用的字符编码，在计算机系统中使用一个字节（8位）来表示一个字符，共包含128个字符的编码。
- Unicode是一种更广泛的字符编码标准，用来表示世界上所有符号的字符编码，包括了ASCII编码中的字符。Unicode编码可以使用不同的标志符，如UTF-8、UTF-16等，来表示不同的字符。

在计算机系统中，数字和字符的互换可以通过字符编码表进行转换。字符编码表将每个字符映射为对应的二进制数值，从而实现字符与数字之间的相互转换。

原补反码

原码：加一个符号位，其1表示负数，0表示正数（如+1000=01000；-1000=11000）
反码：正数反码和原码一样，负数除去符号位都取反（如（-1000）=10111）
补码：正数和原码一样，负数在其反码的基础上加1（如（-1000）=11000）

总结： “即正数原码、反码和补码都一样，负数的反码除去符号位都取反，补码在其反码的基础上再加1即可”

负数的原码和补码加和为0，而不是与反码，与反码的加和为所有位都为1，所以负数存储实际是靠补码，补码是负数真实表示

注意区分符号位与有效数字，一般表示的都是有效数字，在用三码表示时，就需要在其基础上增添一位符号位 

负数反码取反，不取反符号位

运算

符号位加有效数字

加减法

利用补码进行减法，就是被减数和减数在相减时，把减数连带着减号转化为负数，进而为补码，然后让被减数与其进行二进制加法，就是最终结果

计算1101-1011，1101补码为01101，-1011补码为10101，相加为00010

进制转换

十进制小数转二进制 

二进制保留8位小数，就是，二进制小数点后，保留8个位

十进制小数点前的转二进制，不断地除以2，看余数

小数点后的转二进制，不断乘以2，看结果是否超过1 

二进制转十六进制，就是4位4位取然后转化 

在涉及十进制时，每位上记录的数，是余数，是余数，如果能整除，那么该位上就没有数字，为0

注意不够一组4位时，就自动补齐0 

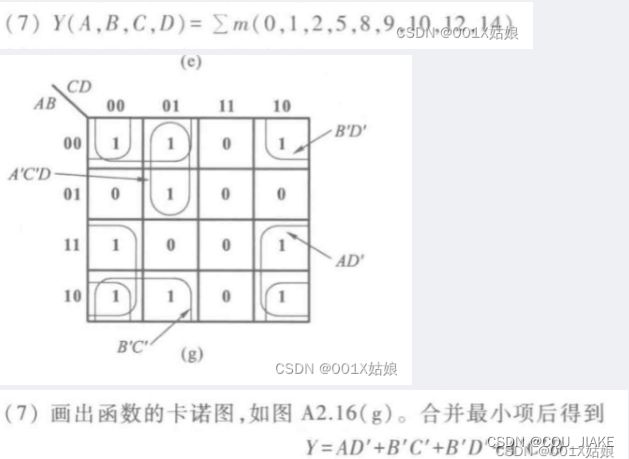
化简

在卡诺图中，每两个相邻格子消掉一个变量；相邻格子意为与该变量的两个取值均为1，所以结果与其无关，可以消掉

所以本质上就是在卡诺图中，找不变的量

串联起不同化简方式的方法就是真值表，通过直接得到真值表，

将逻辑表达式转化为由卡诺图的形式

对于这个卡诺图，需要注意以下四个角，四个角落连在一起也是一个表达式 

组合逻辑电路

根据逻辑功能的不同特点，可以将数字电路分为两大类，一类为组合逻辑电路，一类为时序逻辑电路，前者不具有记忆功能，也就是任何时刻的输出仅仅取决于该时刻的输入，与电路原来的状态无关，即电路中不包含存储单元；而时序逻辑电路具有记忆功能，这是与组合逻辑电路最不同的一点。

组合逻辑电路的分析方法

从电路的输入到输出逐级写出逻辑函数式，得到Y
利用公式法或者卡诺图化简法进行化简
可以转换为真值表的形式

组合逻辑电路的基本设计方法

进行逻辑抽象
写出逻辑函数式
选定器件类型
将逻辑函数化简或转换成适当的描述形式
根据化简或转换后的逻辑式，画出逻辑电路的连接图
设计验证
工艺设计

常用的组合逻辑电路模块

普通编码器
编码器的功能就是将输入的每一个高、低电平信号编成一个对应的二进制代码。其本质就是赋予二进制代码特定含义的过程，一般分为普通编码器和优先编码器两类。
普通和优先的区别在于普通编码器要求只输入一个有效编码信号，而优先编码器允许多个有效编码信号的输入，但是我只会从优先级最高的那个开始，比如3-8线优先编码器，则最先从I7开始编码。

译码器

将每个输入的二进制代码译成对应的输出高、低电平信号或另外一个代码，因此，译码是编码的反操作。常用的译码器有二进制译码器、二-十进制译码器和显示译码器三类。

加法器（原理必须掌握！）

比如说1001和0111相加，图中（1）这个位置也就是1和1相加后向它的高位也就是（2）进了1，（1）这里并没有考虑低位的进位（直接相加），而在（2）这个位置，它考虑了（1）位置的进位1，后面的（3）位置或者更高位也都要考虑来自低位的进位，所以我们把不考虑低位的进位实现半加运算的电路称为半加器，把考虑低位进位的称为全加器。
半加器由一个异或门和一个与门组成。）这里的S是相加后本位的结果，而CO是相加后本位向高位的进位。

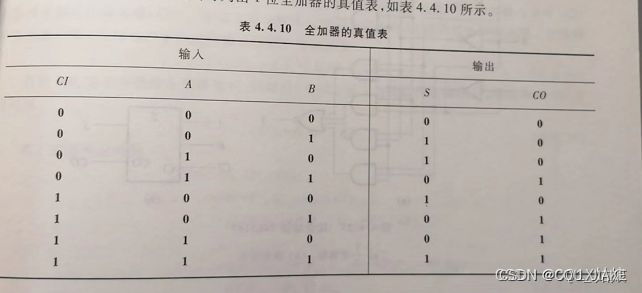
1位全加器：除去最低位外，每一位都考虑来自低位的进位。（多了一个输入进位端CI）
即两个对应位的加数和低位的进位3个数相加。所用电路称为全加器。其中CI为低位向本位的进位，S为相加后本位的结果，CO为本位向高位的进位。

 

 

如果理解了1位半加器的话，那么1位全加器也不难理解，它只是多了一个低位向高位的进位CI，本质还是不变，比如，表中第5行，A=0，B=0，A+B本应该为0的，但是CI为1，也就是低位向高位进一，所以最后的结果为A+B+CI=1，再比如A=0, B=1, CI=1时，A+B=1，但是低位向本位进1，所以最后的结果为1+0+1=10，S为0，本位向高位进1，CO为1。

数值比较器（了解即可~）

作用如其名，就是用来比较两个数值的大小。两个数比较大小，一定有三种结果，大于、等于和小于。
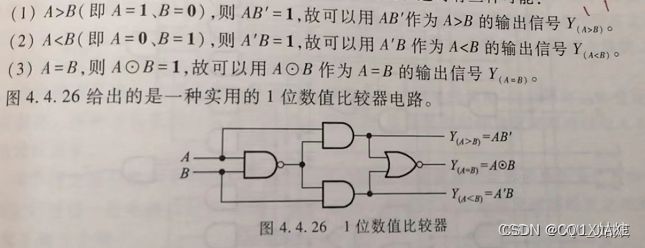
1位数值比较器

> 多位数值比较器
比较两个多位数的大小时，必须自高而低逐位比较，只有在高位相等时，才需要比较低位。比如ABC和DEF，首先比较A和D，如果A>D，那么ABC>DEF，如果A=B，则需进行B和E的比较，反之，若A

组合逻辑电路中的竞争-冒险

竞争
在组合逻辑电路中，当某一个变量经过两条以上路径到达输出端时，由于每条路径上的延迟时间的不同，到达终点的时间有先后，这一现象称为竞争。（输入级）

冒险
由于竞争使电路的输出端出现了稳态下没有的干扰脉冲（毛刺）的现象称为冒险。（输出级）

竞争-冒险
由于竞争而在电路输出端可能产生尖峰脉冲的现象称为竞争-冒险。可以这样理解，本来最终结果应该都为0的，但是出现了一小段的1（也就是出现了本不该在理论设计中出现的脉冲干扰信号）。

判别竞争-冒险

只要输出端的逻辑函数在一定条件下可以简化为Y=A+A’或Y=AA’，则可判定存在竞争-冒险现象。
比如某个电路输出逻辑函数表达式为Y=AB+A’C，此时判断它是否存在竞争-冒险现象，不可以对表达式进行化简，观察有没有一个变量同时出现了原状态和非状态，然后保持这个变量不变，其它变量取0和1的组合，例如：当B=C=1时，上式将成为Y=A+A’，也就是存在竞争冒险现象。

5. 消除竞争-冒险现象的方法

接入滤波电容
引入选通脉冲
修改逻辑设计，增加冗余项
 

针对verliog

异步同步

状态机三段论

序列检测

分频，取模

状态机

if,case

for不考