MATLAB 抽取与内插处理
MATLAB 抽取与内插处理
多速率信号处理是指对同时存在两种及以上数据速率的系统进行处理。多速率信号处理的核心操作是抽取、内插、低通滤波。本次主要介绍如何让利用MATLAB进行抽取和内插处理。
1.整数倍抽取
当信号的抽样数据量太大时,为了减少数据量以便处理和计算,在抽样数据中每隔(D-1)个取一个数据。此处D是一个整数,这样的抽取称为整数倍抽取,D称为抽取因子。通常用符号”↓D“表示将抽样频率降为原来的1/D。一般在抽取之前对信号进行低通滤波,也就是抗混叠滤波措施,把信号的频带限制在抽取后频率的一半以下(因为根据抽样定理,此时信号的频率顶多为抽取后频率的一半,正好先滤除带外噪声)。
2.整数倍内插
内插是先在已知抽样序列的相邻两个抽样点之间等间隔的插入(I-1)个零值点,然后进行低通滤波,即可求得I倍内插得结果。那么对数据进行整数倍零值内插后,信号的特性会发生什么改变呢?
假设某一个系统中,模拟信号只在0~1KHZ的频段内有信号,利用2KHZ的频率进行抽取,则抽取后的信号没有频谱混叠,频谱周期为2KHZ,信号的频谱图如图1(a)所示。根据整数倍零值内插规则,对抽样数据进行2倍零值内插后,其信号频谱图如图1(b)所示。
粗略地看,两者的频谱图没什么不同。但需要注意的是,内插前的信号抽样频率为2KHZ,2倍零值内插后的信号速率为4KHZ,频谱周期为4KHZ。如果再2倍零值内插后增加一级低通滤波器(其截止频率为1KHZ),则滤波后的频谱周期依然为4KHZ。只是滤掉了频率在1~3KHZ之间频谱成分,则滤波后的频谱变成图1(d)所示的样子,而这正是使用4KHZ速率对原始模拟信号进行抽样后的信号频谱。信号的时域与频域是一一对应的,也就是说,通过整数倍零值内插、低通滤波处理后,即可得到正确的经高速抽样后的数字信号。
3.采用MATLAB仿真整数倍抽取前后的信号频谱
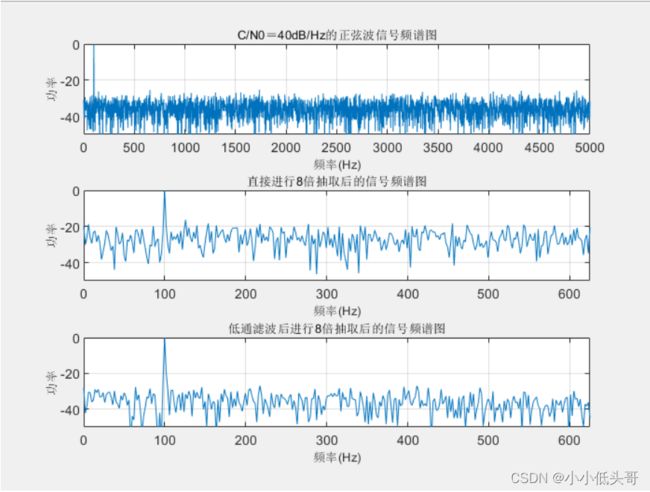
假设原始信号是频率为100HZ的正弦波信号,要求仿真产生载噪比(C/N0)为40dB/HZ的正弦波信号,初始抽样频率为10kHZ。仿真直接对信号进行8倍抽取后的信号频谱,以及先进行低通滤波(截止频率为625HZ),再进行8倍抽取后的信号频谱。比较抽取前后,以及滤波前后的频谱变化情况。
% 用Matlab仿真整数倍抽取前后的信号频谱图。
% 载噪比=log10(信号功率Ps/噪声单边功率谱密度Pn0);
clear all
%定义参数
f = 100; %原始信号频率100HZ
fs = 10000; %初始采样频率为10KHZ
t = 0:1/fs:0.5; %采样时长
N0 = 1; %噪声信号功率谱密度为0dBW/Hz
PN0 = N0*fs; %噪声的功率=单边功率谱密度*带宽
Ps = 10^(40/10)*N0; %信号功率 40=10log10(Ps/N0)
D=8; %抽取倍数
%定义信号 并给予相应功率
s = sin(2*pi*f*t); %正弦波 功率为1/2;
s = sqrt(2*Ps)*s; %功率为1/2*2*Ps=Ps
noise = randn(1,length(t)); %产生方差为1 均值为0 功率为1W的高斯白噪声序列
noise = sqrt(PN0)*noise; %功率为PN0的噪声
sin_noise = s + noise; %产生带有加性高斯白噪声的正弦信号序列
sin_noise=sin_noise/max(abs(sin_noise));%归一化处理
%归一化不影响载噪比 载噪比等于信噪比 * 带宽
%s = s/max(abs(sin_noise));noise = noise/max(abs(sin_noise));
%P1 = sum(s.^2)/length(s);
%P2 = sum(noise.^2)/length(noise);
%求的 log10(P1/(P2)*fs) == 载噪比 因此归一化不影响载噪比
%求幅频响应
Spec_sin_noise = 20*log10(abs(fft(sin_noise)));
Spec_sin_noise = Spec_sin_noise - max(Spec_sin_noise);
%方案1:直接抽进行D倍抽取后的信号
d2=sin_noise(1:D:length(t));
Spec_d2 = 20*log10(abs(fft(d2)));
Spec_d2 = Spec_d2 - max(Spec_d2);
%方案2:sin_noise先经低通滤波器后抽取
b = fir1(80,625/(fs/2)); %采用频率为fs时 截止频率设为为625HZ(抽取后的抽样频率值的半)
%也就是先滤波掉最后抽取之后得到的抽样频率以外的噪声
%或直接wn = (抽取后的抽样频率/2)/(fs/2)=(抽取后的抽样频率/fs)=(fs/D)/fs=1/D
%即b = fir1(80,1/D);
FilterS=filter(b,1,sin_noise);%对原始信号进行低通滤波
%滤波后抽取 并求幅度响应
Fd2 = FilterS(1:D:length(FilterS));
Spec_Fd2 = 20*log10(abs(fft(Fd2)));
Spec_Fd2 = Spec_Fd2 - max(Spec_Fd2);
%画图
%f = x / N * Fs; %f为实际频率 x表示FFT输出的序列号 N表示FFT长度 Fs表示采样频率
%x = 0:length(Spec_sin_noise)-1;
%x = x/length(x)*fs;
x = 0:fs/length(Spec_sin_noise):fs-fs/length(Spec_sin_noise);
subplot(311); plot(x,Spec_sin_noise); axis([0 fs/2 -50 0]);
xlabel('频率(Hz)','fontsize',8); ylabel('功率','fontsize',8);
title('C/N0=40dB/Hz的正弦波信号频谱图','fontsize',8);grid;
x = 0:(fs/D)/length(Spec_d2):(fs/D)-(fs/D)/length(Spec_d2);
%x=0:length(Spec_d2)-1;
%x=x/length(x)*Fs/D;
subplot(312); plot(x,Spec_d2); axis([0 fs/2/D -50 0]);
xlabel('频率(Hz)','fontsize',8); ylabel('功率','fontsize',8);
title('直接进行8倍抽取后的信号频谱图','fontsize',8);grid;
x = 0:(fs/D)/length(Spec_Fd2):(fs/D)-(fs/D)/length(Spec_Fd2);
%x=0:length(Spec_Fd2)-1;
%x=x/length(x)*Fs/D;
subplot(313); plot(x,Spec_Fd2); axis([0 fs/2/D -50 0]);
xlabel('频率(Hz)','fontsize',8); ylabel('功率','fontsize',8);
title('低通滤波后进行8倍抽取后的信号频谱图','fontsize',8);
grid;
关于载噪比和信噪比的一些概念可以看这篇信噪比和载噪比_赤豆几维的博客-CSDN博客
3.1 结果展示
从图中可以明显看出,不经过抗混叠滤波处理而直接进行抽取的信号载噪比比较低,经过滤波处理再进行抽取的信号的载噪比更高。
4.采用MATLAB仿真整数倍内插过程得信号变换关系
假设原始信号是频率为100HZ的正弦波信号,初始抽样频率为800HZ。仿真对信号进行8倍内插后的信号波形。比较内插前后信号时域波形的变换。
%My_E6_2_InterSpec.m;
%定义参数
f = 100; %信号频率为100HZ
fs = 800; %抽样频率为800HZ 则f最大不能超过fs/2
I = 8; %内插倍数为8
%产生信号
t = 0:1/fs:0.5;
si = sin(2*pi*f*t);
%进行8倍零值内插处理
Isi = zeros(1,length(si)*I);
Isi(1:I:length(Isi)) = si;
%经低通滤波器
%因为信号最高频率为fs/2,所以内插后的截止频率为fs/2
%b = fir1(80,(fs/2)/(fs*I/2));
b = fir1(80,1/I);
FilterS = filter(b,1,Isi);
FilterS = FilterS/max(abs(FilterS));
%画图
figure(1)
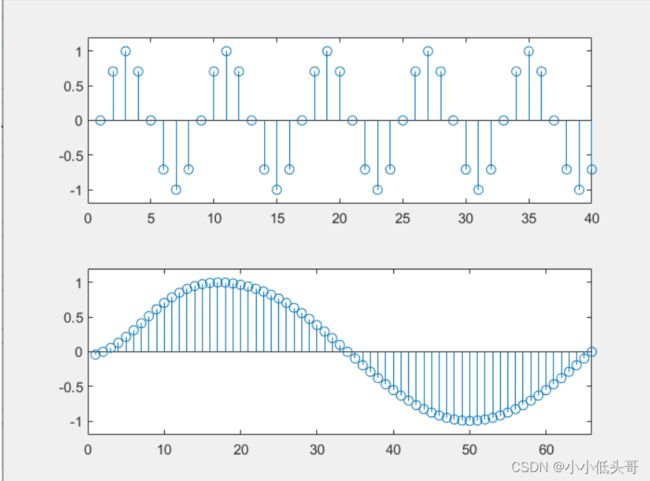
subplot(211);stem(si(1:40));axis([0 40 -1.2 1.2]);%
subplot(212);stem(FilterS(40:105));axis([0 66 -1.2 1.2]);
%求幅频响应
f_si = 20*log10(abs(fft(si,512))); %原始信号
f_si = f_si - max(f_si);
f_Isi = 20*log10(abs(fft(Isi,512))); %直接内插后的信号
f_Isi = f_Isi - max(f_Isi);
f_FilterS = 20*log10(abs(fft(FilterS,512)));%内插并滤波后的信号
f_FilterS = f_FilterS - max(f_FilterS);
x1 = 0:fs/length(f_si):fs-fs/length(f_si);
figure(2)
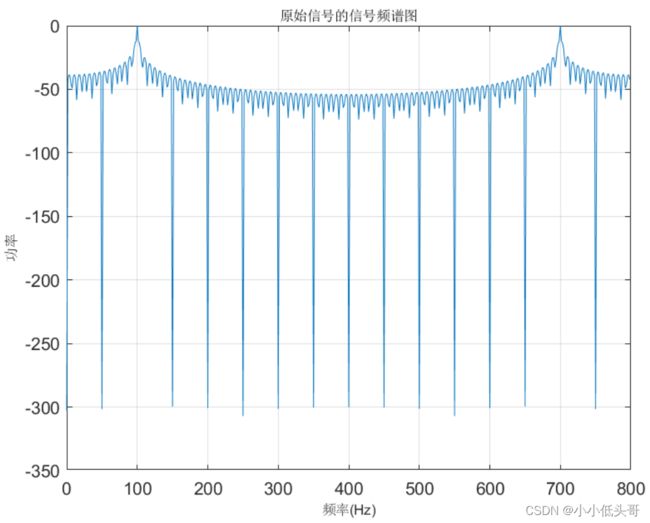
plot(x1,f_si);
xlabel('频率(Hz)','fontsize',8); ylabel('功率','fontsize',8);
title('原始信号的信号频谱图','fontsize',8);grid;
x2 = 0:fs*I/length(f_FilterS):fs*I-fs*I/length(f_FilterS);
figure(4)
plot(x2,f_FilterS);
xlabel('频率(Hz)','fontsize',8); ylabel('功率','fontsize',8);
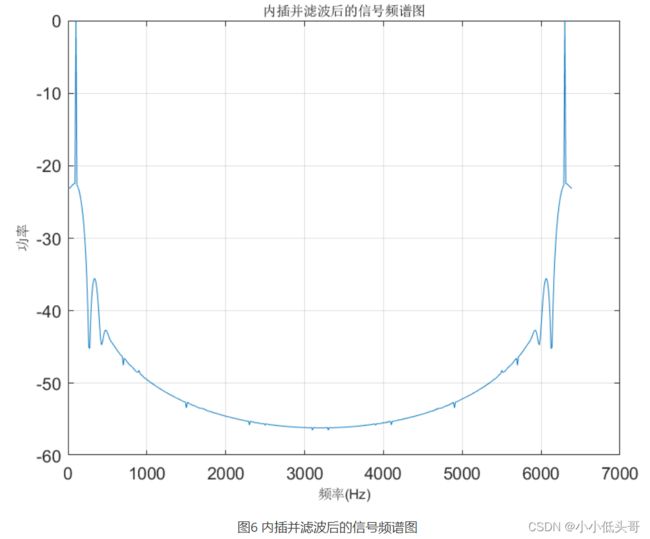
title('内插并滤波后的信号频谱图','fontsize',8);grid;
figure(3)
x2 = 0:fs*I/length(f_FilterS):fs*I-fs*I/length(f_FilterS);
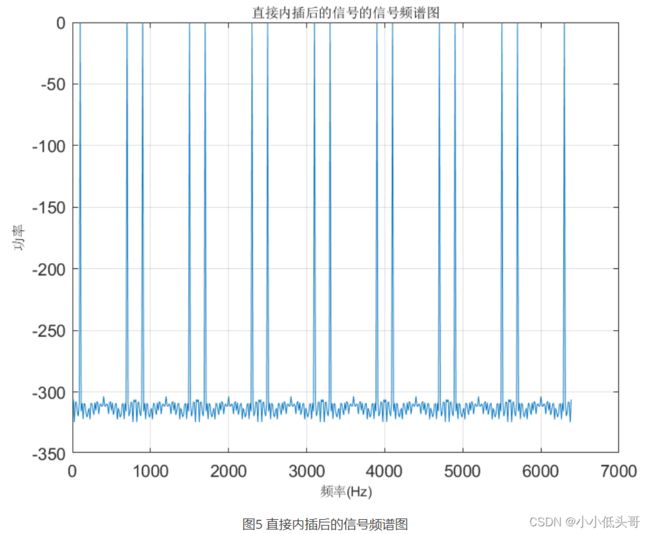
plot(x2,f_Isi);
xlabel('频率(Hz)','fontsize',8); ylabel('功率','fontsize',8);
title('直接内插后的信号的信号频谱图','fontsize',8);grid;
4.1结果展示
由运行结果可是,经8倍零值内插及低通滤波处理后,已经形成了正确的6.4KHZ抽样信号。
对比图4、5、6,验证了2中的结论。即图4中抽样频率为800HZ的信号,经8倍内插后,抽样频率变成了6.4KHZ,并且频谱图是原始信号的频谱图的周期扩展。滤波后整个信号的抽样频率还是6.4KHZ,但是滤掉了原始抽样频率范围外的噪声。整体的流程就相当于使用了6.4KHZ的抽样频率采集频率原始正弦信号。
5.比值为有理数的频率转换
单独的抽取滤波器和内插滤波器只能实现整数倍的频率转换。对于比值为有理数的频谱转换,可以采用先内插后抽取的方法,直接实现频率比值为有理数的转换,根据整数倍抽取及内插的原理,速率转换过程中均需使用低通滤波器作为抗混叠滤波器,因此设计一个截止频率为而二者带宽最小值的滤波器即可。