数据的机器级表示
 1.1 信息的二进制编码
1.1 信息的二进制编码
(1)计算机内部所有的信息都用二进制(即:0和1)进行编码
(2)机器级数据分两大类;
数值型数据:可用来表示数量的多少,可比较其大小,分整数和实数
整数:分无符号整数和带符号整数,用定点数表示
实数:用浮点数表示
非数值型数据:辑数(包括位串)、西文字符和汉字。
(3)信息的二进制编码
真值和机器数:
真值:机器数真正的值,即现实世界中带正负号的数例如(-1,2)
机器数:数值数据在计算机内部编码表示的数称为机器数,也即用0和1编码的计算机内部的0/1序列
给定一个0/1序列,在未确定采用什么进位记数制、定点还是浮点表示以及编码表示方法之前,它所代表的的数值数据的值是无法确定
例如::机器数 01011001的值是多少? 答案:不知道!
1.2 数制和编码
(1)进位计数数制
两个基本要素:基数和权
基数:数制中所用到的不同数码的个数 例如:10进制 0-9
权:不同数位的固定常数 例如 1234 百位权为10^2 十位权为10^1
(2)计算机中常用的进位计数制
书写规范: 加数字下标 加字母后缀
例如:101011.1001B(二进制)、29.03125D(十进制)
(3)数制间的转换
十进制整数转换为任意进制整数(除基取余法)从下至上
十进制小数转换为任意进制小数(乘基取整法)从上至下
1.3 定点与浮点表示(小数点的处理)
(1)定点数与浮点数
小数点约定在固定的位置的数称为定点数
小数点约定为可浮动的数称为浮点数
(2)定点表示
定点小数(一般用来表示浮点数的尾数):小数点总是固定在数的最左边
定点整数(表示整数):小数点总是固定在数的最右边
(3)浮点表示
在基数R一定的情况下:
M的位数决定了数的表示精度
E的位数决定了数的表示范围,其值确定了小数点的位置。
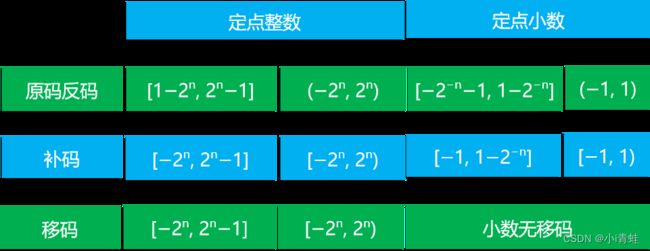
(4)定点数的编码表示(符号的处理)
原码表示法
由符号位直接后跟数值位构成,因此也称“符号-数值” (Sign and Magnitude )表示法;(正数与负数仅仅符号位不同、数值位部分完全相同)
小数原码的定义
例如,若x1= +0.1011, x2= -0.1011,字长为8位
[x1]原= 0.1011000 [x2]原= 1+0.1011000 = 1.1011000
整数原码的定义
例如,若x1= +1011,x2= -1011,字长为8位,(共n+1位字长)
[x1]原= 000001011 [x2]原= 2^7+0001011 = 10001011
零的原码表示不唯一 ,0的补码、移码表示唯一;
例2:写出机器字长8位,原码表示所对应的十进制整数和小数的表示范围。
整数范围:-127≤x ≤ +127 或:-128 < x <+128
小数范围: -(1-2-7 ) ≤ x ≤ 1 -2-7 或: -1<x <+1
补码表示法
重要概念:在一个模运算系统中,一个数与它除以“模”后的余数等价。
移码表示法(搜索学习
移码与补码,仅符号位相反,其余各位相同;
2.1 整数的表示
(1)无符号整数 (没有符号位)
常在一个数的后面加一个“u”或“U”表示无符号数; 12345U, 0X2B3Cu
(2)带符号整数 (一般用补码表示)

2.2 浮点数的表示格式(即规格化)
(1)右规: 当有效数位进到小数点前面时,需要进行右规,如 +/-1.bbbbX2E (b为0或1) 右规时,尾数每右移一位,阶码加1,直到尾数变成规格化形式为止
右规时指数会增加,因此可能会溢出
(2)左规 当出现形如+/-0.0….bb…bX2E(b为0或1)时,需要进行左规
左规时,尾数每左移一位,阶码减1,直到尾数变成规格化形式为止