卷积神经网络实现手势图像的识别

零、数据集及工具

传送门
数据集用的是搭建DNN时使用的手势识别图像。
提取码：pcoi

一、原理和框架

这篇文章的卷积网络模型基于LeNet-5，也就是
$input\to conv1\to relu\to maxpool1\to conv2\to relu\to maxpool2\to fc3\to fc4\to output(softmax)$

前向传播好好写，反向传播用框架实现，是现在最主流的方式，快捷不容易出错。
我搭建CNN用到TensorFlow深度学习框架，首先来简单说明一下tf.nn中函数的用法。

• 卷积层：tf.nn.conv2d(x, w, strides=[1,stride,stride,1], padding="SAME/VALID")
• 激活：tf.nn.relu(x)
• 池化层：tf.nn.max_pool(x, ksize=[1,f,f,1], strides=[1,stride,stride,1], padding="SAME/VALID)
• 展开：tf.contrib.layers.flatten(x)
• 全连接层：tf.contrib.layers.fully_connected(x, num_neuron, activation_fn=None/tf.nn.relu)

二、图像预处理（归一化和独热编码）

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
import h5py
import cnn_utils

train_x, train_y, test_x, test_y, classes = cnn_utils.load_dataset()
index = 5
plt.imshow(train_x[index])
print("y =", np.squeeze(train_y[: ,index]))
print("train_x.shape:", train_x.shape)

# 图像归一化
train_x1 = train_x / 255
test_x1 = test_x / 255

# 标签独热编码
train_y1 = cnn_utils .convert_to_one_hot(train_y, 6).T
test_y1 = cnn_utils .convert_to_one_hot(test_y, 6).T

print("训练集样本数：", train_x1.shape[0])
print("测试集样本数：", test_x1.shape[0])
print("训练集图像：", train_x1.shape)
print("训练集标签：", train_y1.shape)
print("测试集图像：", test_x1.shape)
print("测试集标签", test_y1.shape)

训练集样本数： 1080
测试集样本数： 120
训练集图像： (1080, 64, 64, 3)
训练集标签： (1080, 6)
测试集图像： (120, 64, 64, 3)
测试集标签 (120, 6)

注意：这和深层神经网络不一样，不需要 将RGB三维图片降维，然后将多样本列堆叠起来！ 只需要图像归一化，标签独热编码即可。

三、CNN搭建过程函数

# placeholder
def create_placeholder(n_H0, n_W0, n_C0, n_y):
    X = tf.placeholder(tf.float32, [None, n_H0, n_W0, n_C0])
    Y = tf.placeholder(tf.float32, [None, n_y])
    
    return X, Y

# 初始化过滤器
def initialize_parameters():
    # [n_H, n_W, n_C, num] 分别是高 宽 通道数 输出通道数（过滤器数量）
    W1 = tf.Variable(tf.random_normal([4,4,3,8]))
    W2 = tf.Variable(tf.random_normal([2,2,8,16]))
    parameters = {
        "W1": W1,
        "W2": W2
    }
    return parameters

# CNN前向传播
def forward_propagation(X, parameters):
    W1 = parameters["W1"]
    W2 = parameters["W2"]
    # conv1
    Z1 = tf.nn.conv2d(X, W1, strides=[1,1,1,1], padding="SAME")
    A1 = tf.nn.relu(Z1)
    P1 = tf.nn.max_pool(A1, ksize=[1,8,8,1], strides=[1,8,8,1], padding="SAME")
    # conv2
    Z2 = tf.nn.conv2d(P1, W2, strides=[1,1,1,1], padding="SAME")
    A2 = tf.nn.relu(Z2)
    P2 = tf.nn.max_pool(A2, ksize=[1,4,4,1], strides=[1,4,4,1], padding="SAME")
    # FC
    P = tf.contrib.layers.flatten(P2)
    Z3 = tf.contrib.layers.fully_connected(P, 120, activation_fn=tf.nn.relu)
    Z4 = tf.contrib.layers.fully_connected(Z3, 6, activation_fn=None)
    
    return Z4

# 计算成本
def compute_cost(Z4, Y):
    cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(logits=Z4, labels=Y))
    
    return cost

四、整合CNN模型并运行

# model
def model(train_x, train_y, test_x, test_y, lr=0.01, num_epoch=1000, minibatch_size=64, print_cost=True, isPlot=True):
    seed = 3
    costs = []
    (m, n_H0, n_W0, n_C0) = train_x.shape
    n_y = train_y.shape[1]
    X, Y = create_placeholder(n_H0, n_W0, n_C0, n_y)
    parameters = initialize_parameters()
    Z4 = forward_propagation(X, parameters)
    cost = compute_cost(Z4, Y)
    optimizer = tf.train.AdamOptimizer(lr).minimize(cost)
    init = tf.global_variables_initializer()
    with tf.Session() as session:
        session.run(init)
        for epoch in range(num_epoch):
            epoch_cost = 0
            num_minibatches = int(m / minibatch_size)
            seed = seed + 1
            minibatches = cnn_utils.random_mini_batches(train_x, train_y, minibatch_size, seed)
            for minibatch in minibatches:
                (minibatch_x, minibatch_y) = minibatch
                _ , minibatch_cost = session.run([optimizer,cost], feed_dict={X:minibatch_x, Y:minibatch_y})
                epoch_cost += minibatch_cost / num_minibatches
            costs.append(epoch_cost)
            if print_cost:
                if epoch % 10 == 0:
                    print("epoch =", epoch, "epoch_cost =", epoch_cost)
        if isPlot:
            plt.plot(np.squeeze(costs))
            plt.title("learning_rate =" + str(lr))
            plt.xlabel("epoch")
            plt.ylabel("cost")
            plt.show()
        parameters = session.run(parameters)
        
        correct_prediction = tf.equal(tf.argmax(Z4, axis=1), tf.argmax(Y, axis=1))
        accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
        print("训练集准确率：", accuracy.eval({X:train_x, Y:train_y}))
        print("测试集准确率：", accuracy.eval({X:test_x, Y:test_y}))
        
        return parameters

运行网络

parameters = model(train_x1, train_y1, test_x1, test_y1, lr=0.01, num_epoch=1000)

运行结果

epoch = 0 epoch_cost = 6.046239018440247
epoch = 10 epoch_cost = 0.8401443846523762
epoch = 20 epoch_cost = 0.5430787391960621
epoch = 30 epoch_cost = 0.37734642811119556
epoch = 40 epoch_cost = 0.1890146671794355
epoch = 50 epoch_cost = 0.08683486701920629
epoch = 60 epoch_cost = 0.08065505273407325
epoch = 70 epoch_cost = 0.025464061880484223
epoch = 80 epoch_cost = 0.010602715017739683
epoch = 90 epoch_cost = 0.0036894527947879396
epoch = 100 epoch_cost = 0.0024794578494038433
epoch = 110 epoch_cost = 0.0021597172526526265
epoch = 120 epoch_cost = 0.0015165473596425727
epoch = 130 epoch_cost = 0.0012093357254343573
epoch = 140 epoch_cost = 0.0010065358073916286
epoch = 150 epoch_cost = 0.0008580533994972939
epoch = 160 epoch_cost = 0.0006731234116159612
epoch = 170 epoch_cost = 0.000575631856918335
epoch = 180 epoch_cost = 0.0005104850497446023
epoch = 190 epoch_cost = 0.00043178290434298106
epoch = 200 epoch_cost = 0.0003564941771401209
epoch = 210 epoch_cost = 0.0003232461576772039
epoch = 220 epoch_cost = 0.0002740809841270675
epoch = 230 epoch_cost = 0.00025000690584420227
epoch = 240 epoch_cost = 0.00021687703610950848
epoch = 250 epoch_cost = 0.0001856840840446239
epoch = 260 epoch_cost = 0.00016450545490442892
epoch = 270 epoch_cost = 0.00014440709355767467
epoch = 280 epoch_cost = 0.00012826649935959722
epoch = 290 epoch_cost = 0.00011342956258886261
epoch = 300 epoch_cost = 0.0001002715393951803
epoch = 310 epoch_cost = 9.134015908784932e-05
epoch = 320 epoch_cost = 8.081822375061165e-05
epoch = 330 epoch_cost = 7.289223390216648e-05
epoch = 340 epoch_cost = 6.377049851380434e-05
epoch = 350 epoch_cost = 5.675839747709688e-05
epoch = 360 epoch_cost = 5.180321227271634e-05
epoch = 370 epoch_cost = 4.63823556628995e-05
epoch = 380 epoch_cost = 4.153193617639772e-05
epoch = 390 epoch_cost = 3.71186773691079e-05
epoch = 400 epoch_cost = 3.3484795721960836e-05
epoch = 410 epoch_cost = 3.103026369899453e-05
epoch = 420 epoch_cost = 2.7161293019162258e-05
epoch = 430 epoch_cost = 2.424556680580281e-05
epoch = 440 epoch_cost = 2.1611446754832286e-05
epoch = 450 epoch_cost = 1.9845915744554077e-05
epoch = 460 epoch_cost = 1.8085945555412763e-05
epoch = 470 epoch_cost = 1.5999822608137038e-05
epoch = 480 epoch_cost = 1.4649548518264055e-05
epoch = 490 epoch_cost = 1.3234309221843432e-05
epoch = 500 epoch_cost = 1.2474629897951672e-05
epoch = 510 epoch_cost = 1.0769706705104909e-05
epoch = 520 epoch_cost = 9.782952247405774e-06
epoch = 530 epoch_cost = 8.88926402353718e-06
epoch = 540 epoch_cost = 7.897974711568168e-06
epoch = 550 epoch_cost = 7.140903875324511e-06
epoch = 560 epoch_cost = 6.437216967469794e-06
epoch = 570 epoch_cost = 5.833738470073513e-06
epoch = 580 epoch_cost = 5.1959334257389855e-06
epoch = 590 epoch_cost = 4.821698055934576e-06
epoch = 600 epoch_cost = 4.539523985158667e-06
epoch = 610 epoch_cost = 3.980700640227042e-06
epoch = 620 epoch_cost = 3.481204629451895e-06
epoch = 630 epoch_cost = 3.211789177726132e-06
epoch = 640 epoch_cost = 2.829953558602938e-06
epoch = 650 epoch_cost = 2.5407657346931956e-06
epoch = 660 epoch_cost = 2.3277445251324025e-06
epoch = 670 epoch_cost = 2.1203611453302074e-06
epoch = 680 epoch_cost = 1.9698040283344653e-06
epoch = 690 epoch_cost = 1.773695679219145e-06
epoch = 700 epoch_cost = 1.5777209014800064e-06
epoch = 710 epoch_cost = 1.4154058298743166e-06
epoch = 720 epoch_cost = 1.2963970377199985e-06
epoch = 730 epoch_cost = 1.183275156080299e-06
epoch = 740 epoch_cost = 1.0764728379797361e-06
epoch = 750 epoch_cost = 9.585948674839528e-07
epoch = 760 epoch_cost = 8.798984154623213e-07
epoch = 770 epoch_cost = 7.984745433731177e-07
epoch = 780 epoch_cost = 7.096832543851406e-07
epoch = 790 epoch_cost = 6.668258656361559e-07
epoch = 800 epoch_cost = 5.947650230098134e-07
epoch = 810 epoch_cost = 5.503942883677837e-07
epoch = 820 epoch_cost = 4.884115956116375e-07
epoch = 830 epoch_cost = 4.476663146846249e-07
epoch = 840 epoch_cost = 4.0949880464324906e-07
epoch = 850 epoch_cost = 3.703167985591449e-07
epoch = 860 epoch_cost = 3.326482138632514e-07
epoch = 870 epoch_cost = 3.079016703821935e-07
epoch = 880 epoch_cost = 2.7876461317077883e-07
epoch = 890 epoch_cost = 2.5039257511849655e-07
epoch = 900 epoch_cost = 2.313004827669829e-07
epoch = 910 epoch_cost = 2.083001673369722e-07
epoch = 920 epoch_cost = 1.8619790820295634e-07
epoch = 930 epoch_cost = 1.7819851949596455e-07
epoch = 940 epoch_cost = 1.5779258788484185e-07
epoch = 950 epoch_cost = 1.4289144134593812e-07
epoch = 960 epoch_cost = 1.29137815108038e-07
epoch = 970 epoch_cost = 1.1575005887110024e-07
epoch = 980 epoch_cost = 1.0703554642610413e-07
epoch = 990 epoch_cost = 9.53940206827042e-08

训练集准确率： 1.0
测试集准确率： 0.875

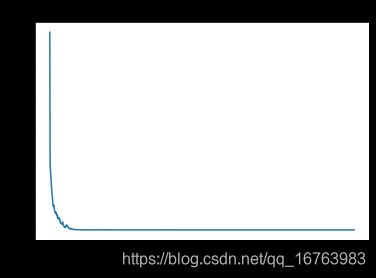
训练集上acc=100%，测试集上acc=87.5%，已经是较好的训练结果了。考虑到训练集和测试集之间相差12.5%，属于方差较大的误差类型，可以通过正则化等方式防止过拟合，所以进一步改进可以考虑L2正则化、dropout、数据增强等方法。

五、预测

和写DNN时的预测一个原理，将输入图像的维度修改正确，正向传播得到Softmax结果，argmax函数定位最大概率的位置，与实际标签对比，计算准确度。

index = 999
 
x = tf.placeholder(tf.float32, [None, 64, 64, 3])
plt.imshow(train_x[index])
image = train_x[index].reshape(1, 64, 64, 3)
print(image.shape)
init = tf.global_variables_initializer()

with tf.Session() as session: 
    session.run(init)
    image_prediction = session.run(forward_propagation(x, parameters), feed_dict={x: image})
    prediction_label = np.squeeze(session.run(tf.argmax(image_prediction))) # argmax取softmax分类后向量最大位置
    print("prediction_label:", prediction_label)
    true_label = np.squeeze(train_y[: ,index])
    print("true_label:", true_label)
    if prediction_label == true_label:
        print("预测结果正确！")
    else:
        print("预测结果错误！")

【写预测这部分代码时遇到一些BUG待修复】

FailedPreconditionError: Attempting to use uninitialized value fully_connected_48/biases
	 [[{{node fully_connected_48/biases/read}}]]