安全算法(二):共享密钥加密、公开密钥加密、混合加密和迪菲-赫尔曼密钥交换
安全算法(二):共享密钥加密、公开密钥加密、混合加密和迪菲-赫尔曼密钥交换
本章介绍了共享密钥加密、公开密钥加密,和两种加密方法混合使用的混合加密方法;最后介绍了迪菲-赫尔曼密钥交换。
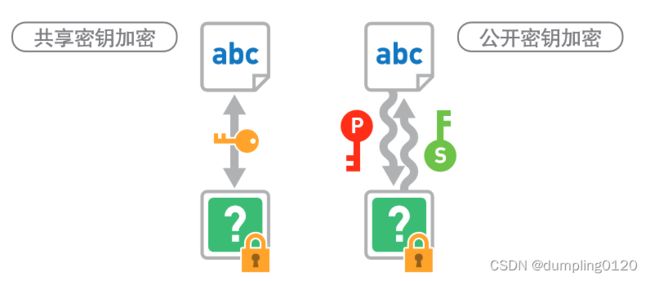
加密数据的方法可以分为两种:加密和解密都使用相同密钥的“共享密钥加密”和分别使用不同密钥的“公开密钥加密”。以下将分别介绍。
共享密钥加密
共享密钥加密是加密和解密都使用相同密钥的一种加密方式。由于使用的密钥相同,所以这种算法也被称为**“对称加密”**。
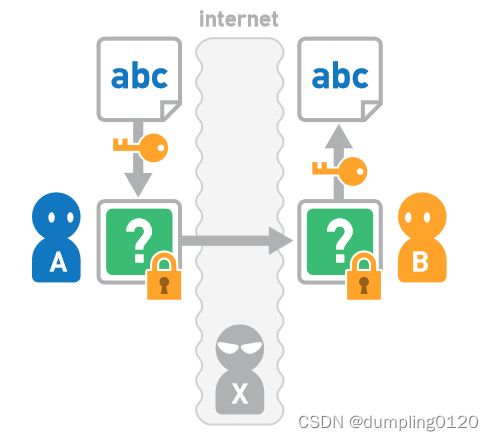
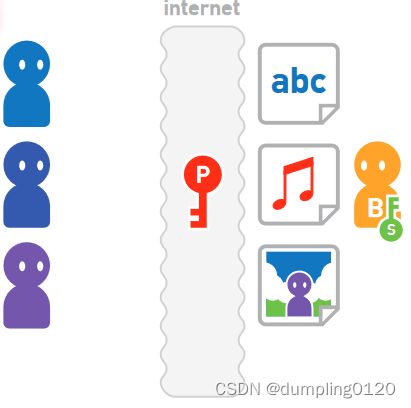
假设 A 准备通过互联网向 B 发送数据。由于有被窃听的风险,所以需要把想要保密的数据加密后再发送。A使用密钥加密数据后再发送给B。B 收到密文后,使用相同的密钥对其进行解密。这样,B 就取得了原本的数据。只要是加密好的数据,就算被第三者恶意窃听也无须担心。
*实现共享密钥加密的算法有凯撒密码、AES、DES、动态口令等,其中 AES 的应用最为广泛。
AES: Advanced Encryption Standard
DES: Data Encryption Standard
共享密钥加密中存在的问题
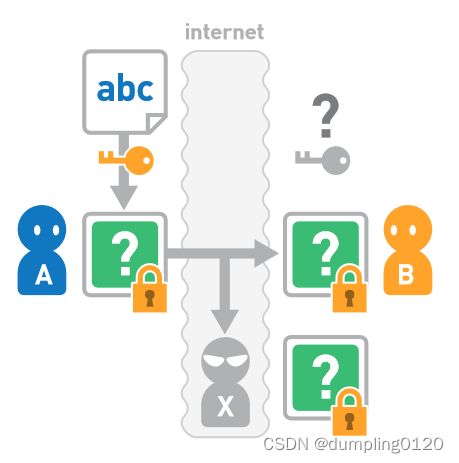
B收到A发送密文时,密文可能已经被窃听。假设A和B无法直接沟通,B不知道加密时使用的什么密钥。A 需要通过某种手段将密钥交给 B。和密文一样,A 又在互联网上向 B 发送了密钥。B 使用收到的密钥对密文进行解密。但是,该密钥也有可能会被 X 窃听。这样一来, X 也可以使用密钥对密文进行解密了。
为了解决这个问题,需要找到可以把密钥安全送出的方法,即“密钥分配问题”。要想解决这个问题,可以使用**“密钥交换协议”和“公开密钥加密”**两种方法。
公开密钥加密
公开密钥加密是加密和解密使用不同密钥的一种加密方法。由于使用的密钥不同,所以这种算法也被称为“非对称加密”。加密用的密钥叫作**“公开密钥”**,解密用的叫作“私有密钥”。
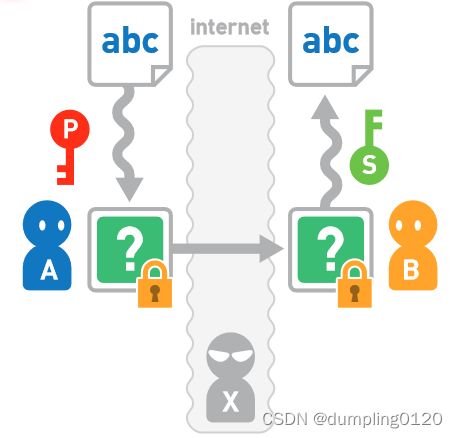
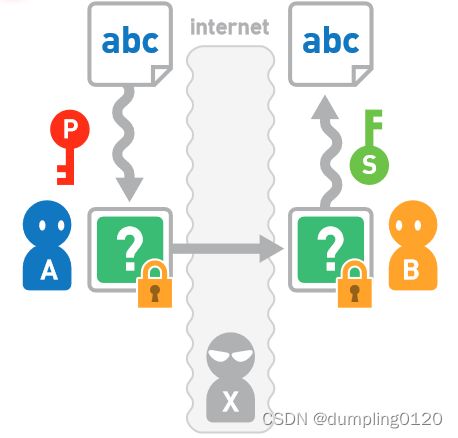
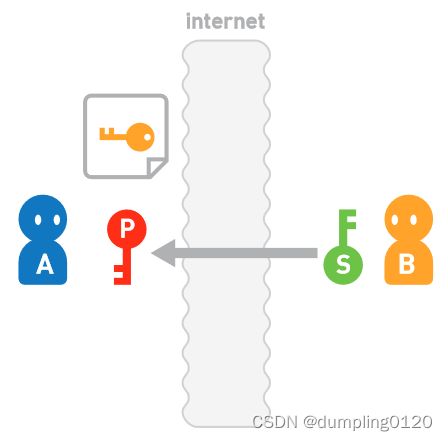
假设 A 准备通过互联网向 B 发送数据。首先,需要由接收方 B 来生成公开密钥 P 和私有密钥 S 。然后把公开密钥发送给A。A 使用 B 发来的公开密钥加密数据。A 将密文发送给 B,B 再使用私有密钥对密文进行解密。这样,B 就得到了原本的数据。
*实现公开密钥加密的算法有RAS 算法、椭圆曲线加密算法等,其中使用最为广泛的是 RSA 算法。
与共享密钥加密不同的是, 公开密钥加密不会出现密钥分配问题。
公开密钥和密文都是通过互联网传输的,因此可能会被 X 窃听。但是,使用公开密钥无法解密密文,因此 X 也无法得到原本的数据。
此外,在和多人传输数据时,使用公开密钥加密十分方便。
公开密钥是不怕被人知道的,所以 B 可以把公开密钥发布在网上。与此相反,私有密钥不能被人知道,必须严密保管。假设有许多人都想向 B 发送数据。想发送数据的人首先在网上取得 B 发布的公开密钥。然后用它加密要发送的数据。最后把密文发给 B。
B 用私有密钥对收到的密文进行解密,取得原本的数据。这种情况就不需要为每个发送对象都准备相对应的密钥了。需要保密的私有密钥仅由接收方保管,所以安全性也更高。
公开密钥加密中存在的问题
“中间人攻击“
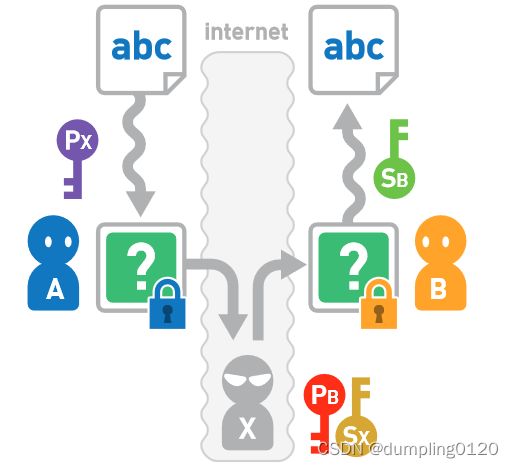
X 把公开密钥 PB 替换成自己的公开密钥 PX。A 使用公开密钥 PX 对数据加密。当A把想要给B的密文发送出去后,X接收了这个密文。这个密文由X 生成的公开密钥PX 加密而成,所以 X 可以用自己的私有密钥 SX 对密文进行解密。接下来,X 用 B 生成的公开密钥 PB 加密数据。X把密文发送给B,这个密文由B发出的公开密钥PB 加密而成,所以B可以用自己的私有密钥 SB 来解密。
从收到密文到解密密文都没发生任何问题,因此 B 也意识不到数据已经被窃听。
公开密钥的可靠性会出现问题,就是因为 A 无法判断收到的公开密钥是否来自 B。要想解决这个问题,就要用到之后会讲到的**“数字证书”**。
公开密钥加密还有一个问题,那就是加密和解密都比较耗时,所以这种方法不适用 于持续发送零碎数据的情况。要想解决这个问题,就要用到**“混合加密”**。
*考虑到加密所需的计算流程,算法必须满足如下条件。
① 可以使用某个数值对数据进行加密(计算)。
② 使用另一个数值对加密数据进行计算就可以让数据恢复原样。
③ 无法从一种密钥推算出另一种密钥。
混合加密
共享密钥加密存在无法安全传输密钥的密钥分配问题,公开密钥加密又存在加密解密速度较慢的问题。结合这两种方法以实现互补的一种加密方法就是混合加密。
在混合加密中,要用处理速度较快的共享密钥加密对数据进行加密。不过,加密时使用的密钥,则需要用没有密钥分配问题的公开密钥加密进行处理。
使用处理速度较快的共享密钥加密对数据进行加密。加密时所用的密钥在解密时也要用到,因此 A 需要把密钥发送给 B。将密钥通过公开密钥加密进行加密后,A 就可以将其安全地发送给 B 了。因此,作为接收方,B 需要事先生成公开密钥 P 和私有密钥 S 。然后,B 将公开密钥发送给 A。
A 使用收到的公开密钥,对共享密钥加密中需要使用的密钥进行加密,并将加密后的密钥法发送给B。B 使用私有密钥对密钥进行解密。
接下来,A 只要将使用这个密钥加密好的数据发送给 B 即可。加密数据时使用的是处理速度较快的共享密钥加密。
像这样,混合加密在安全性和处理速度上都有优势。能够为网络提供通信安全的 SSL 协议也应用了混合加密方法。SSL 是 Secure Sockets Layer(安全套接层)的简写,该协议经过版本升级后,现在已正式命名为 TLS(Transport Layer Security,传输层安全)。但是,SSL 这个名字在人们心中已经根深蒂固,因此该协议现在也常被称为 SSL 协议或者 SSL / TLS 协议。
迪菲-赫尔曼密钥交换
迪菲 - 赫尔曼(Diffie-Hellman)密钥交换是一种可以在通信双方之间安全交换密钥的方法。这种方法通过将双方共有的秘密数值隐藏在公开数值相关的运算中,来实现双方之间密钥的安全交换。
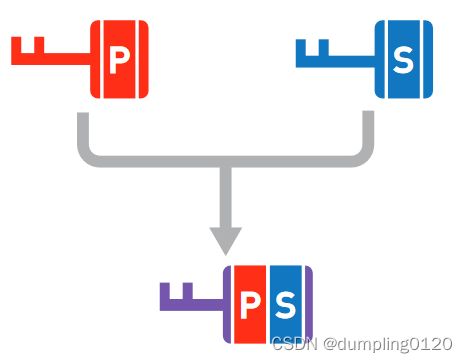
假设有一种方法可以合成两个密钥。使用这种方法来合成密钥 P 和密钥 S,就会得到由这两个密钥的成分所构成的密钥 P-S。这种方法有三个特征:
一、即使持有密钥 P 和合成的密钥 P-S, 也无法把密钥 S 单独取出来。即密钥之间可以合成,但不能分解。
二、不管是怎样合成而来的密钥,都可以把它作为新的元素,继续与别的密钥进行合成。即使用密钥 P 和密钥 P-S,还能合成出新的密钥 P-P-S。
三、密钥的合成结果与合成顺序无关,只与用了哪些密钥有关。如下图。
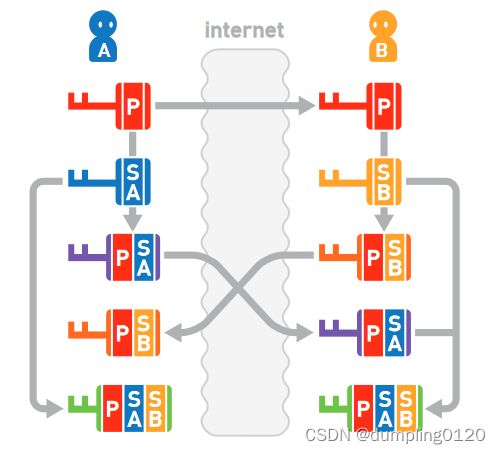
应用实例:
通过图示方法,A 和 B 都得到了密钥 P-SA-SB。这个密钥将作为 “加密密钥”和“解密密钥”来使用。
由于密钥无法被分解, 所以 X 无法取得私有密钥 SA 和 SB。在公开的密钥中,X无法用自己 窃听到的密钥合成出 P-SA-SB,因此这种交换方式是安全的。
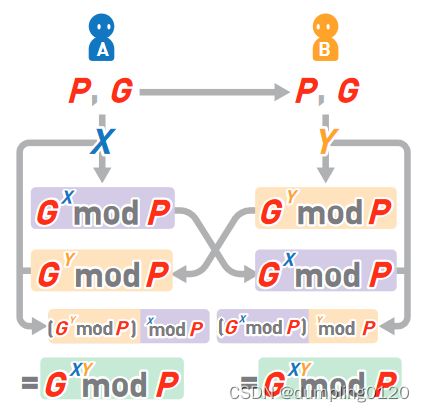
以上用公式来表示这种密钥交换法。用 P、G 两个整数来表示一开始生成的公开密钥 P。其中 P 是一 个非常大的素数,而 G 是素数 P 所对应的生成元(或者“原根”)中的一个。
A 和 B 分别准备了各自的秘密数字 X 和 Y。X 和 Y 都必须小于 P-2。
A 和 B 分别计算“(G 的 秘密数字次方)mod P”。mod 运算就是取余运算 。“ G mod P”就是计算G 除以P 后的余数。此处的运算等同于概念意义上的“合成”
然后,A和B交换以上计算结果,并计算这个值的秘密数字次方,然后再mod P。最后会得到相同结果。
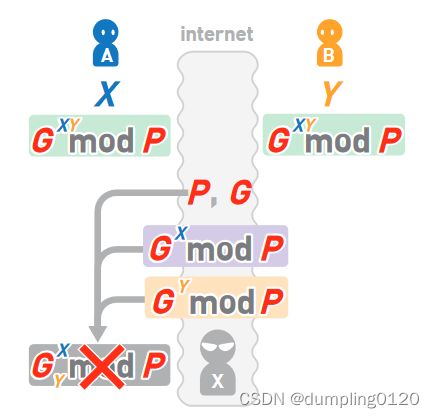
同理,窃听者X无法获得最终结果。
*根据素数 P、生成元 G 和“G^X mod P”求出 X 的问题就是“离散对数问题”,人们至今还未找到这个问题的解法,而迪菲 - 赫尔曼密钥交换正是利用了这个数学难题。
实际上,双方并没有交换密钥,而是生成了密钥。因此,该方法又被叫作**“迪菲 - 赫尔曼密钥协议”**。
参考资料:我的第一本算法书 (石田保辉 宮崎修一)